车载炮射击密集度逐步回归分析
2012-12-25王晓锋徐亚栋
曹 宁,王晓锋,徐亚栋,尹 强
(南京理工大学 机械工程学院,南京210094)
车载炮战略和战术机动性强,具有快速反应能力、精确打击能力和自主作战能力,能满足现代高科技局部战争对火炮战略机动性及战术机动性的要求,对车载炮武器系统进行射击精度分析,寻找影响射击精度的主要因素,能为新型车载炮总体方案论证、总体设计,射击法则的制定以及有效地发挥车载炮射击效率提供合理的依据.射击精度包括射击准确度和射击密集度,前者描述了落点平均位置对瞄准点的系统性偏差,后者描述了落点的随机散布特性.
车载压制火炮射击密集度的确定方法随着理论和技术水平的发展得到了进一步的完善.如,潘玉田等[1]推导出了有脱靶弹的立靶密集度估计公式;王兆胜等[2]讨论了诸元精度、射程、密集度对弹丸首发命中概率的影响;闫雪梅等[3]建立了计算射程及密集度分组试验的Bayes估计方法;文献[4]分析了地面密集度随射角和初速的变化规律;马春茂等[5]研制了某自行高炮车炮系统的射击密集度预测软件.
本文采用回归分析法研究随机因素对车载炮射击密集度的影响,通过对射程和各因素进行标准化,使各种因素量纲得到一致,从而可通过比较回归系数大小来反映与该系数对应因素的重要性.建立了随机因素影响程度逐步回归分析算法,以某车载炮的密集度性能实弹射击试验数据为基础,建立了落点数据的相关系数与射击密集度之间的统计关系,并分析了各因素对该车载炮射击密集度的影响.
1 逐步回归分析算法
假定车载炮发射一组n发弹丸,共有l种因素xj(j=1,2,…,l)影响其落点坐标,现已获得各射弹的落点坐标(Xi,Zi),i=1,2,…,n.如何分析这些因素对车载炮射击精度的影响及其影响程度,这就必须对所获得的数据进行统计分析,本文采用逐步回归分析法对此进行分析.由于对X和Z所采用的回归原理相同,以X为例进行说明.为使各种因素量纲得到一致,对射程X和因素xj进行标准化处理.
将得到的数据(xi1,xi2,…,xil,Xi)进行标准化:
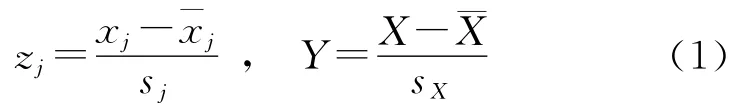
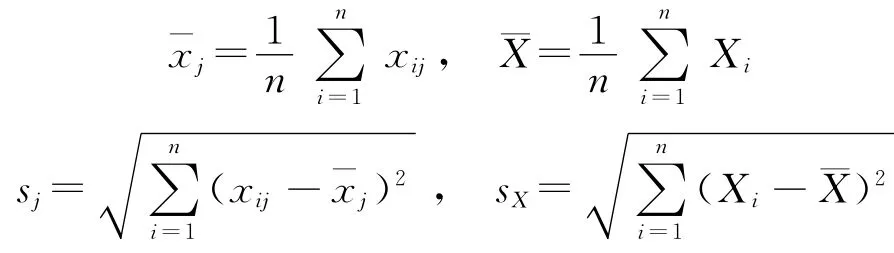
经标准化变换后,zj和Y的几何平均值为0,标准离差为1,则标准化后的多元回归方程可表示为

式中,β0为常数项,βj为Y对因素zj的回归系数,εY为随机误差.
将得到的数据经式(1)变换后,代入式(2)得:
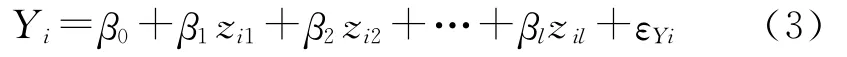
这里假定εYi为独立同分布,其均值为0,其方差σ2未知,但0<σ2<∞.对式(3)进行最小二乘估计,可得βj的估算值j:式中,j(j=1,2,…,l)为标准化回归系数,)称为相关系数矩阵,D=(dj)为右端列阵)为标准化回归系数列阵.
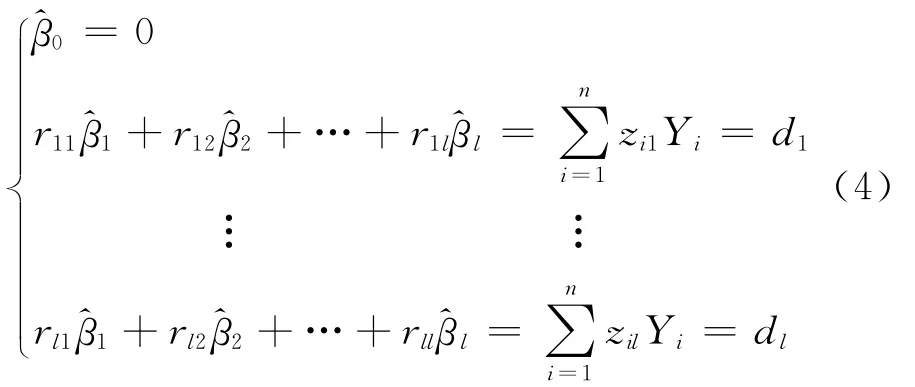
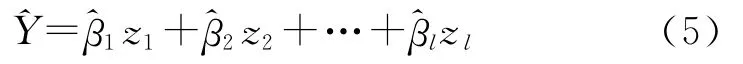
以上给出了多元线性回归分析的一般形式,本文将给出逐步回归分析的基本算法流程.令:

记开始时,对总因素数重新赋值ml=l,令迭代步数p=1,回归方程中的因素数U=0.
逐步回归分析法的基本原理:在考虑的全部因素中按其对X的作用大小、显著程度大小或者贡献大小,由大到小地逐个引入回归方程,而对X作用不显著的因素始终不被引入回归方程.另外,己被引入回归方程的因素在引入新因素后也可能失去重要性,而需要从回归方程中剔除出去.引入一个因素或者从回归方程中剔除一个因素都称为逐步回归的一步,每一步都要进行F分布的检验,以保证在引入新因素前回归方程中只含有对X影响显著的因素,而不显著的因素已被剔除.
步骤1 对不包含在回归方程中的ml个因素,计算偏回归平方和
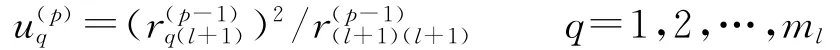
假定第m个因素的偏回归平方和值最大,即),该因素zm对的回归贡献最大,于是优先考虑选入zm.
步骤2 对引入因素zm进行显著性检验.令U=U+1,计算统计量:
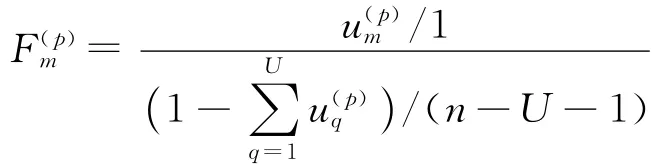
给定显著水平α、自由度1和n-U-1,得F1,n-U-1(α),若<F1,n-U-1(α),则不引进,此时由于贡献度最大的因素zm都不能引进,其它因素也就不能引进,计算结束.若>F1,n-U-1(α),表明引入的因素zm对回归方程的贡献是显著的,应引进.并对引进因素zm对应中的主元m进行如下变换,得到变换后的
求解式(6)时一定要遵循以下次序:①非主元m所在行、列,即k≠m、j≠m;②主元m所在行(除主元外),即k=m,j≠m;③主元m所在列(除主元外),即k≠m,j=m;④主元m,即k=m,j=m.
一旦确定zm要引进回归方程,必须利用引进zm后已经变换的,按前面相同的方法对回归方程中已存在的其它因素逐一进行显著性检验,以确定由于因素zm的引进是否需要将其它因素从回归方程中保留或剔除.
步骤3 因素zm(z(U)=zm)引入后的回归方程.标 准 回 归 系 数 为
标准回归方程为
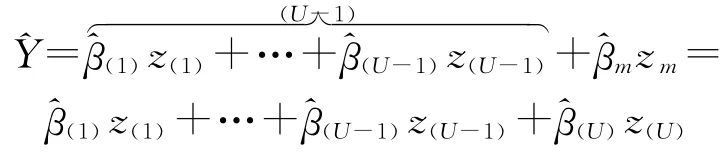
一般回归方程为
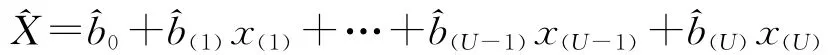
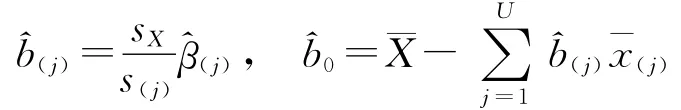
2 靶场试验数据的相关性分析
为了考察某车载炮的密集度性能,对其进行了实弹射击试验.表1给出了5组、每组7发射弹落点坐标(Xc,Zc)的数据和对应的密集度估计值.由表可见,前3组射击密集度非常差,后2组密集度较好.为此对这5组数据中的落点坐标(X,Z)进行了相关性分析,其相关系数值也在表中给出.对有限射弹的数量,若相关系数|rXZ|≥0.8,则认为X和Z有强的相关性;若0.3≤|rXZ|<0.8,则认为有弱的相关性;若|rXZ|<0.3,则认为没有相关性.前2组的相关性强,密集度很差;后2组相关性弱,密集度很高.为此,图1给出了该车载炮射击试验落点数据的相关系数|rXZ|与射击密集度之间的统计关系图.图中,MX为纵向密集度,MZ为横向密集度.
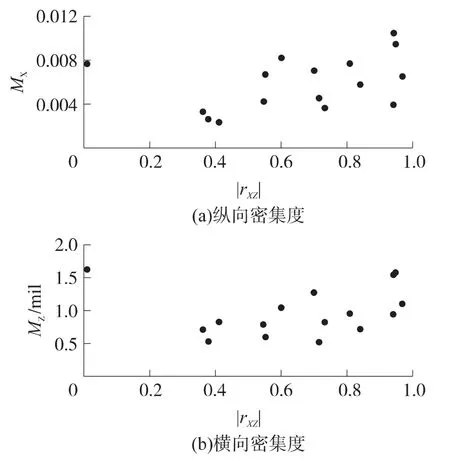
图1 相关系数与密集度的统计关系
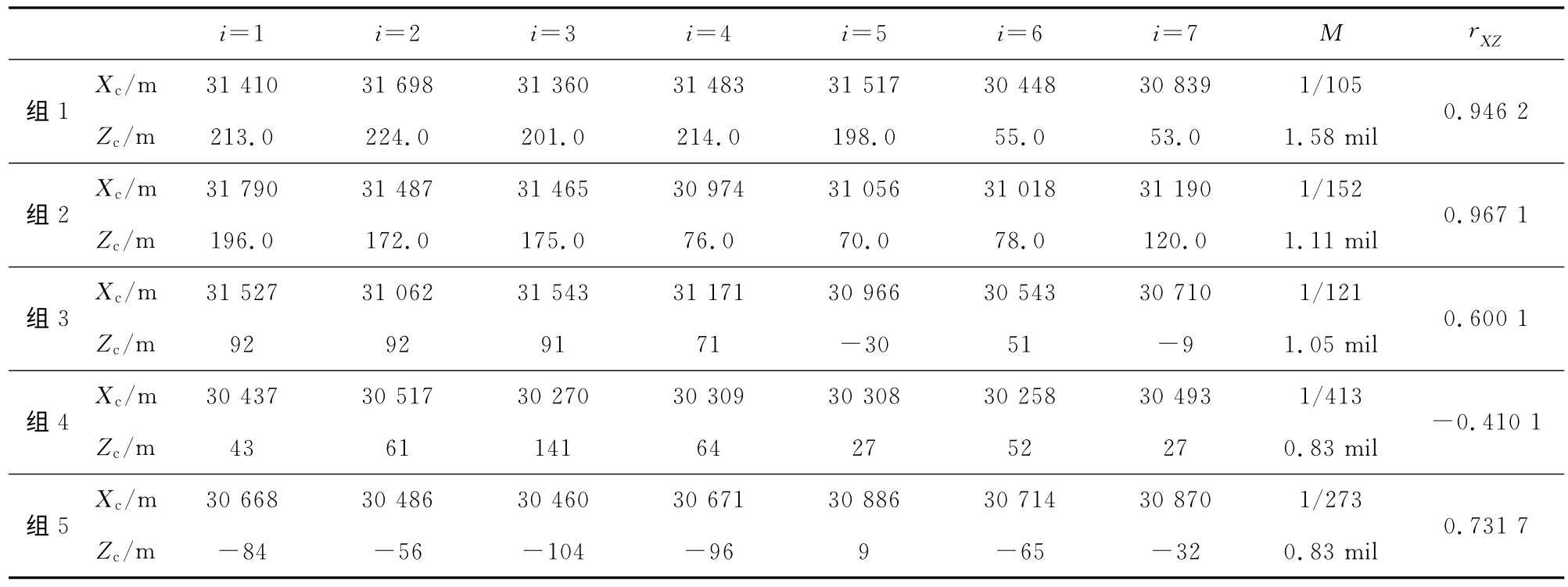
表1 弹落点坐标数据和密集度估计值
从统计结果可以看出,密集度越高,相关系数|rXZ|越小;反之,密集度就越低,|rXZ|就越大.同时还可以看出,较小的相关系数,不能保证有较高的射击密集度.对其它射击试验的结果进行分析,也得出同样的结论,如表2所示.若一组弹丸的落点坐标(Xc,Zc)存在较强的相关性,即|rXZ|≥0.8,表明车载炮武器系统存在严重的系统干扰,应加以认真检查.
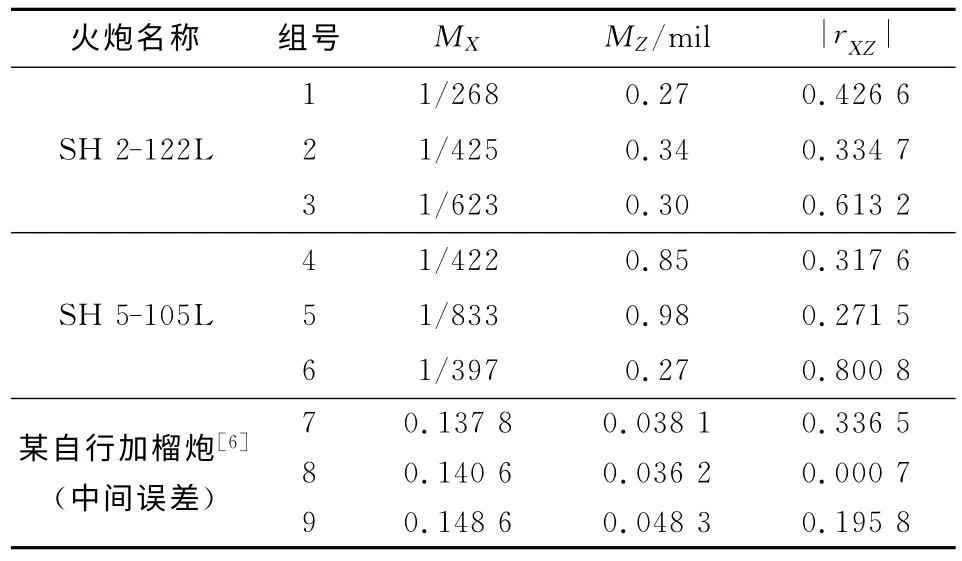
表2 密集度与相关系数的关系
3 射击密集度影响因素逐步回归分析
前文对某车载炮密集度实弹射击试验数据进行了相关性分析,下面以第一组的数据为例进行密集度影响因素的回归分析.回归方程包含的因素越多,回归平方和越大,剩余的平方和越小,剩余均方也随之愈小,预测值的误差也愈小,模拟的效果愈好.但是方程中的因素过多,预报工作量就会越大,其中有些相关性不显著的预报因子会影响预测的效果.因此,在多元回归模型中,选择适宜的因素数目尤为重要.本例中,由于测试条件的局限性选择因素数目为6.第一组的试验测试结果见表3.表中,v0为弹丸初速,mq为弹丸质量(kg),Iq为转动惯量比,εe为弹丸偏心距(mm),p31为驻退机腔3和腔1室的压力之差(MPa),σh1为高低机齿弧与齿轮相接触处齿弧侧面法向应力(MPa).因而,一般回归方程的形式为
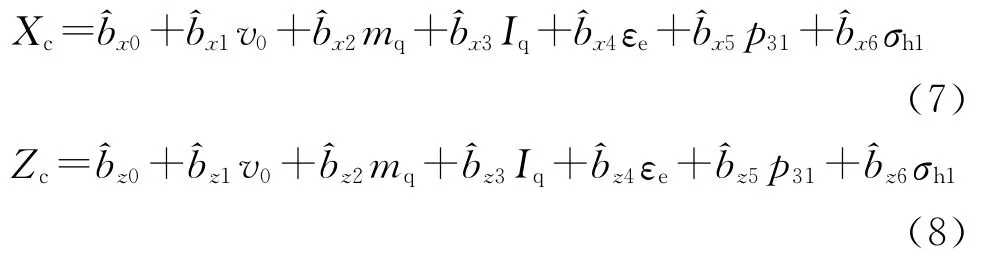
选择v0、mq、εe作为考察因素的理由是很显然的,而选择p31的原因是试图通过该因素的变化来研究后坐阻力对射击密集度的影响,选择σh1的原因是试图通过该因素来反映身管高低指向的变化规律对密集度的影响.
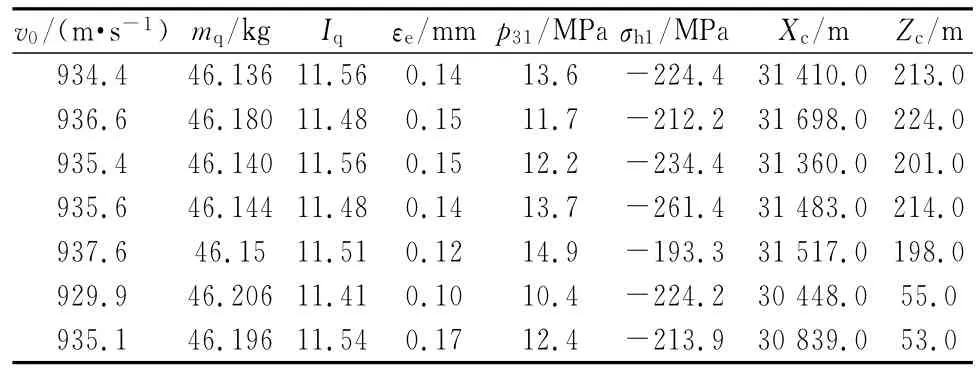
表3 弹丸落点实弹数据表
下面对试验数据进行逐步回归分析,将数据分别代入变换式(1),这样式(7)和式(8)转换成标准的回归方程.经最小二乘法运算,其相关系数矩阵为

从中可以看出:
①Xc与Zc的相关系数rXZ=0.946 2,根据相关性检验,可知Xc与Zc相关.
②初速v0和弹质量mq均分别与驻退机腔室压力p31、射程Xc与Zc相关,这符合实际情况.
③转动惯量比Iq与弹丸偏心距εe相关,这符合实际情况.
④Iq、εe与射程关系不密切,p31与射程有一定的相关性,σh1与射程无相关性.
分别对Xc和Zc进行逐步回归分析,得到Xc与Zc的回归方程分别为
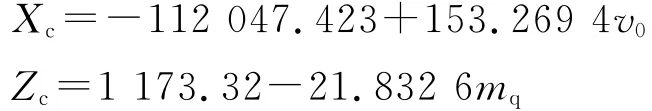
由逐步回归分析结果可以看出,考虑v0、mq、Iq、εe、p31和σh1等因素时,影响弹丸纵向射程的主要因素是初速,影响横向侧偏的主要因素是弹质量.对其它组数据分析亦有类似结果.
4 结束语
本文以某车载炮的密集度性能实弹射击试验数据为基础,采用逐步回归分析法对车载炮射击密集度的影响因素进行分析,给出了该车载炮射击试验落点数据的相关系数与射击密集度之间的统计关系.研究了弹丸初速、弹质量和弹丸偏心距等因素对车载炮射击密集度的影响.回归分析结果表明,影响弹丸纵向射程的主要因素是初速,影响横向侧偏的主要因素是弹质量,与实弹射击结果相吻合,验证了本文所提逐步回归分析法用于车载炮射击精度影响因素分析的可行性和有效性.
[1]潘玉田,马新谋.自动火炮射弹密集度估计[J].火炮发射与控制学报,2006,(2):38-42.PAN Yu-tian,MA Xin-mou.Shot density estimation of automatic gun[J].Journal of Gun Launch & Control,2006,(2):38-42.(in Chinese)
[2]王兆胜,郭锡福.诸元精度与密集度对命中概率的影响[J].弹道学报,2003,15(1):64-68.WANG Zhao-sheng,GUO Xi-fu.Influence on hitting probability by accuracy of firing data and dispersion[J].Journal of Ballistics,2003,15(1):64-68.(in Chinese)
[3]闫雪梅,文艳,邱丛礼.射程与密集度分组试验的Bayes估计[J].弹道学报,2006,18(2):80-83.YAN Xue-mei,WEN Yan,QIU Cong-li.Bayesian estimation of range and dispersion of grouping trial[J].Journal of Ballistics,2006,18(2):80-83.(in Chinese)
[4]王兆胜.射角和初速对地面密集度的影响[J].火炮发射与控制学报,2008,(4):1-4.WANG Zhao-sheng.Influence of departure angle & muzzle-velocity on ground density[J].Journal of Gun Launch & Control,2008,(4):1-4.(in Chinese)
[5]马春茂,孙逢春,李魁武,等.自行高炮车炮系统射击密集度预测研究[J].兵工学报,2002,23(2):251-254.MA Chun-mao,SUN Feng-chun,LI Kui-wu,et al.A prediction on the dispersion accuracy of the gun-vehicle system in self-propelled[J].Acta Armamentarii,2002,23(2):251-254.(in Chinese)
[6]邱瑾,牟少锋,杨军.自行火炮自动瞄准精度数据分析[J].火力与指挥控制,2007,32(1):105-107.QIU Jin,MOU Shao-feng,YANG Jun.Data analysis for aiming accuracy of self-propelled gun[J].Fire Control and Command Control,2007,32(1):105-107.(in Chinese)
