新结构药型罩射流对等效前舱的抗干扰研究

肖强强，黄正祥，祖旭东，朱传胜

（南京理工大学 智能弹药国防重点学科实验室，南京210094）

聚能射流具有速度快、能量密度高、穿透能力强等特点，因此聚能装药战斗部被广泛应用于各种导弹、鱼雷、炮弹等弹药系统中，用于对付坦克、舰船及轻型装甲车辆，还可作为串联攻坚战斗部的前级对付机场跑道、地面建筑、碉堡、掩体等硬目标.聚能射流在飞行过程中极易受到干扰，而导弹、鱼雷、末制导炮弹等探测和制导装置常位于战斗部的前部，且距离药型罩底部较近，聚能射流在穿过前舱的过程中未完全成型，射流头部被前舱消耗，同时产生的碎片等对其进行干扰，容易导致射流发生断裂失稳现象.为了获得较好的侵彻能力，聚能射流的头部速度和断裂时间应尽可能大[1，2]，因此前舱严重影响了聚能射流的破甲威力.

为了降低前舱对聚能射流的干扰，本文设计了一种新结构药型罩，通过在主药型罩顶部增加一个小锥角罩，利用小锥角罩形成的高速射流破坏前舱结构，为主射流顺利通过前舱提供通道，以保证主射流的侵彻威力.

本文利用AUTODYN－2D仿真软件计算了有限长杆体以不同速度侵彻前舱时消耗的杆体长度，以虚拟原点法和准定常侵彻理论为基础，将前舱等效为一定厚度的均质靶板，建立了聚能射流侵彻前舱后计算射流参数的工程算法.通过对常规药型罩和新结构药型罩进行仿真计算，分析射流通过前舱后的头部速度和剩余能量，获得了聚能射流穿过等效前舱后的参数，并与理论分析进行了对比.同时，利用计算得到的射流参数对2种结构药型罩射流穿过等效前舱后对混凝土的侵彻孔形进行了计算.

对2种结构药型罩进行了侵彻带等效前舱钢筋混凝土试验.试验结果表明，采用常规药型罩结构的聚能装药，其形成的射流在穿过前舱后对钢筋混凝土靶板的穿深只有2.28m；新结构药型罩形成的射流，由于前舱已被小射流破坏，大大降低了其对主射流的干扰，主射流顺利穿透2.5m厚的钢筋混凝土靶.试验结果与理论结果基本吻合.

1 聚能射流侵彻带等效前舱混凝土分析

聚能射流头部速度高、尾部速度低，因此在飞行和侵彻过程中，射流会不断拉伸，射流长度不断增加.由连续射流侵彻的准定常理论可知，聚能射流的侵彻深度与其长度成正比.随着射流的继续拉伸，开始出现颈缩断裂现象，射流断裂后，侵彻能力大大降低.因此聚能装药战斗部有一最有利炸高，一方面能够使射流充分伸长，提高侵彻深度；另一方面防止炸高过大使得射流产生径向分散和摆动，甚至出现断裂现象，降低破甲能力.

为了节省弹内空间，弹药系统中聚能装药战斗部距离前舱较近.聚能射流侵彻前舱时，射流未经充分拉伸，甚至还没有完全成型，射流直径较大，侵彻界面处射流速度下降较快，射流能量被大量消耗.由于射流直径较大，侵彻过程中距离侵彻轴线较近的前舱结构与射流接触，而射流与前舱的相对速度较高，因此射流在前舱部件的纵向切割下稳定性降低；同时侵彻过程中产生的大量碎片也会对射流的稳定性产生影响.通过上述分析可以看出，聚能射流穿过前舱后头部速度降低，侵彻混凝土靶时不能充分拉伸，前舱与聚能射流的作用时间越长，越容易发生断裂失稳现象，致使聚能射流的侵彻能力下降.

由于前舱结构复杂，难以对射流侵彻前舱进行理论计算，采用数值仿真软件进行计算费时费力，而且对于不同的聚能装药结构，需要分别对其侵彻前舱过程进行计算.为了计算聚能射流穿过前舱后的参数，将前舱等效为一定厚度的均质靶板，根据聚能射流的虚拟原点法计算其穿过均质等效靶板后的参数，用以计算射流穿过前舱后对混凝土的侵彻孔形.

采用AUTODYN－2D仿真软件，令一与聚能射流相同材料的有限长杆体以不同速度vi（i＝1，2，…，n）沿射流侵彻通道侵彻前舱，杆体的长度足够长，以避免稀疏波在杆底反射.

聚能射流头部侵彻前舱时，若着靶时射流速度为vT0，至射流穿过前舱速度下降至vT，因此可取长杆体速度vi＝vT0～vT.由于射流头部速度较高，可不考虑侵彻过程中侵彻体及靶板强度的影响.针对不同长杆体速度vi，计算得到长杆体侵彻前舱过程中消耗的长度为li.由定常侵彻理论可知，在忽略强度影响的情况下，高速长杆体的侵彻深度与速度无关，因此仅考虑长杆体消耗的长度，不同速度下长杆体消耗长度的平均值为

将前舱等效为厚度为He、密度为ρe的均质靶板，则

式中，由于长杆体采用与射流相同的材料，故ρj为射流和长杆体的密度.

图1为新结构药型罩射流侵彻带前舱等效靶混凝土的示意图.

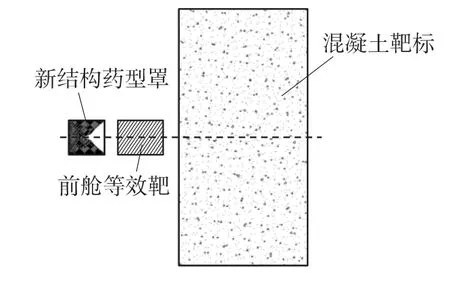
图1 新结构药型罩射流侵彻带前舱等效靶混凝土示意图

为方便利用仿真计算得到的射流参数进行理论计算，设聚能装药起爆时刻为时间坐标零点，空间坐标零点与仿真模型零点重合，本文空间坐标零点为装药顶部.装药高度为L，药型罩底部到前舱的距离为H，（ta，la）为虚拟原点的坐标，由虚拟原点法和准定常侵彻理论可得：

从而得到射流出靶时的头部速度为

假设射流的尾部速度及直径没有受到前舱的影响，则可根据聚能射流穿过前舱后的参数对混凝土的侵彻过程进行计算.

混凝土材料具有低密度、低声速的特点，聚能射流侵彻混凝土材料时射流的头部侵彻速度往往大于混凝土声速.由于靶板材料受到扰动的速度超过材料中扰动的传播速度，因此会在侵彻界面前形成冲击波，对混凝土的扩孔过程产生影响.由于射流直径较细，通常认为，由于射流侧表面的稀疏波的作用，在射流中传播的冲击波很快衰减，传播距离有限，对聚能射流侵彻靶板过程的影响有限，因此可不考虑射流中冲击波的作用.

文献[3，4]通过考虑在靶板中传播的冲击波对侵彻过程的影响，得到了侵彻速度vp大于靶板声速c0时聚能射流的轴向侵彻方程：

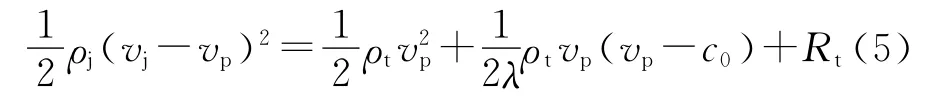
式中，vj为射流着靶速度，vp为侵彻速度，ρt为混凝土的密度，Rt为混凝土靶的侵彻阻抗，c0为零压状态下的混凝土靶声速，λ为常数.

随着侵彻速度的降低，冲击波强度也逐渐降低，至vp≤c0时，侵彻方程退化为A－T方程：

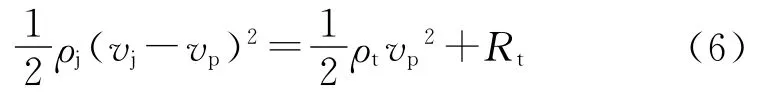
在靶中冲击波的影响下，根据射流速度的不同，扩孔过程[5，6]可分为2个不同阶段，聚能射流最终的侵彻孔直径为

式中，

式中，Dj为射流着靶时的直径；Dm为侵彻孔的最终直径.

铜质射流的密度ρj＝8 930kg/m3，混凝土密度ρt＝2 400kg/m3，侵彻阻抗Rt＝110MPa.GRADY[7]通过试验证实混凝土压力范围在3～25GPa之间时，c0和λ的取值范围为：c0＝3.0～4.1km/s，λ＝1.5～2.2，因此取混凝土状态参数为c0＝3 000 m/s，λ＝1.7.

2 聚能射流侵彻等效前舱的仿真分析

2.1 有限元计算模型及参数

以某战斗部引信与头螺结构为例，对前舱结构进行了简化，计算时只保留对射流干扰较大的部分组件，对于离射流通道较远，对射流干扰小的组件则不予考虑.计算和试验过程中等效前舱材料均为铝材.

前舱采用Lagrange算法，为确定前舱对均质靶的等效厚度，有限长杆也采用Lagrange算法，杆体侵彻前舱过程采用Lagrange/Lagrange耦合算法求解.由于聚能射流的成型过程属于大变形过程，无法采用Lagrange网格对其进行计算，因此射流的成型过程采用AUTODYN－2D的Euler求解器进行计算，射流侵彻前舱过程采用Euler/Lagrange流固耦合算法进行计算.聚能装药选用Octol炸药，药型罩选用高导无氧铜，波形调整器选用尼龙，等效前舱材料为铝，Octol参数见文献[8]，高导无氧铜、尼龙及铝的参数见文献[9].

2.2 聚能射流抗前舱干扰能力的数值计算分析

新结构药型罩和常规药型罩结构的射流形态如图2所示，新结构药型罩在主药型罩的顶部增加了一个小锥角罩，小锥角罩与主药型罩之间采用圆弧过渡连接.炸药起爆后小药型罩首先被压垮形成高速射流，由主药型罩压垮形成的主射流紧随其后.由于小药型罩的直径远小于主药型罩，且小药型罩距离前舱较远，因此小射流侵彻前舱时已完全成型.利用小射流高速侵彻前舱，为主射流开辟通道，降低了前舱对主射流的干扰.

计算过程中，新结构药型罩主罩采用与常规药型罩相同的结构，小锥角罩角度为42°.没有等效前舱的情况下，聚能装药起爆后180μs时，常规药型罩结构射流头部速度为7 245m/s，而新结构药型罩射流头部由小锥角罩压垮形成，因此头部速度比较高，为9 553m/s，对等效前舱有更强的侵彻能力.

图2 聚能装药计算模型及射流形态

2种结构药型罩射流对等效前舱的侵彻过程如图3所示.常规药型罩结构射流头部在起爆后103.7μs开始接触等效前舱，此时射流尚未成型；而新结构药型罩射流由于头部速度较高，91.6μs开始侵彻等效前舱，此时主射流头部刚刚形成，而小射流则已完全成型.

150μs时，随着侵彻过程的进行，小射流被等效前舱消耗完，但主射流已基本成型，常规药型罩结构由于射流头部刚刚形成，因此消耗较多，头部速度降至5 855.8 m/s，等效前舱开始对聚能射流尾部的形成产生干扰.200μs时新结构药型罩主射流已完全成型，等效前舱大部分被破坏，此时主射流仍具有较高的头部速度.

250μs时，新结构药型罩射流穿过等效前舱，结束对等效前舱的侵彻；常规药型罩结构射流直至300μs时才完成对等效前舱的侵彻，新结构药型罩减少了等效前舱对射流的干扰时间.

由于等效前舱对聚能射流头部的消耗，加上对射流成型过程的干扰，射流穿过前舱后出现了严重的颈缩现象，导致其断裂时间提前.

图3 聚能射流侵彻等效前舱作用过程

图4为聚能射流动能Ek随时间的变化曲线.

图4 聚能射流动能变化曲线

没有等效前舱时聚能射流在起爆后190μs完全成型，能量达到最大值，常规药型罩射流能量约为44.5MJ.由于新型药型罩顶部被小锥角罩代替，与常规药型罩相比，主射流能量降低0.5 MJ，约1.1%.但小射流能量为4.36 MJ，远大于主射流能量损失.由于等效前舱对射流能量的消耗，常规药型罩结构射流头部在接触到前舱后能量开始下降，至射流穿过等效前舱，能量消耗了16.1 MJ.与没有前舱相比，聚能射流的头部速度从7 245m/s下降至4 565m/s，能量下降至28.5 MJ，等效前舱消耗了聚能射流总能量的36.1%，大大降低了聚能装药的侵彻威力.

新结构药型罩小射流侵彻等效前舱时，主射流在爆轰气体的作用下能量仍在上升，150μs时主射流开始侵彻等效前舱，能量随着侵彻过程的进行持续降低.由于主射流侵彻等效前舱时已基本成型，因此在侵彻过程中降低了能量消耗，小射流和主射流消耗的总能量只有11.6 MJ，与常规药型罩结构相比降低了30%.

为计算均质铝靶对前舱的等效厚度，用一长度为800 mm的铜质杆体，分别以不同速度沿射流侵彻轴线侵彻等效前舱.图5为杆体速度为8km/s时通过仿真计算得到的侵彻后的长度.

图5 杆体速度8km/s时侵彻等效前舱后的剩余长度

铜质杆体侵彻前舱后消耗的长度如表1所示.

表1 不同速度铜质杆体侵彻前舱后消耗长度

从仿真计算结果可以看出，高速侵彻下，速度变化对杆体消耗长度的影响较小，与第1节中的分析一致.杆体的平均消耗长度＝289mm，均质铝靶的密度ρe＝2 700kg/m3，因此由式（3）可以得到均质等效靶对前舱的等效厚度He＝526mm.

利用仿真计算得到的射流成型参数，对射流侵彻均质等效靶后参数进行了计算，并与射流侵彻前舱后的仿真结果进行了对比.2种药型罩穿过等效前舱后的头部速度vT和直径DT、尾部速度vs和直径Ds、射流长度L及能量Ek如表2所示.

表2 聚能射流穿过等效前舱后的参数

从结果可以看出，将前舱等效为均质等效靶后，理论计算与仿真结果基本上是吻合的，并节省了大量计算时间.与常规药型罩相比，新结构药型罩形成的射流在穿过等效前舱后，头部速度从4 565 m/s提高到5 864 m/s，提高了28.5%；而射流能量从28.5 MJ提高到36.85 MJ，提高了29.3%，采用新结构药型罩，大大提高了射流抗前舱干扰的能力.

3 试验验证

为了验证新结构药型罩对等效前舱的抗干扰能力及侵彻威力，进行了聚能装药侵彻带等效前舱钢筋混凝土试验，常规药型罩结构和新结构药型罩各进行了一发.

聚能装药炸药为Octol，等效前舱材料为铝2A11，钢筋混凝土厚度为2.5 m.常规药型罩结构的侵彻深度只有2.28m，而新结构药型罩在穿过等效前舱后，穿透了2.5 m厚的钢筋混凝土靶，侵彻深度提高了11.7%以上，这表明采用新结构药型罩可明显减少等效前舱对射流的干扰作用.

利用表2中的射流参数对聚能射流侵彻混凝土的侵彻孔直径进行理论计算，详细计算过程可参考文献[10]，不同侵彻深度P处侵彻孔直径DP的试验与计算结果如图6所示，试验结果与理论分析基本上是吻合的.

图6 侵彻孔形的理论计算与试验结果对比

4 结论

为了减少前舱对聚能射流的干扰，提高聚能射流穿过前舱后的侵彻威力，在常规药型罩的顶部增加一小锥角罩，利用小锥角罩形成的小射流清除前舱，为主射流提供通道.

分析了聚能射流侵彻前舱时，将前舱等效为均质靶板的等效方法，针对文中前舱结构，结合数值仿真和理论分析，计算得到了均质等效靶的等效厚度.

由于罩底距离前舱较近，常规药型罩形成的射流侵彻前舱时未经充分拉伸，能量消耗较多.与常规药型罩相比，新结构药型罩形成的射流侵彻等效前舱时能量消耗降低了30%，射流侵彻前舱后，头部速度提高28.5%，能量提高29.3%，具有更强的侵彻能力.

新结构药型罩形成的聚能射流穿过等效前舱后对钢筋混凝土目标的侵彻深度较常规药型罩结构提高了11.7%以上.

采用数值仿真和理论分析相结合的方法，对带前舱聚能装药侵彻混凝土的侵彻孔直径进行了计算，试验与计算结果吻合很好，表明该方法可用于带前舱聚能装药侵彻混凝土的工程计算，满足计算要求.

针对不同的前舱结构，通过对小锥角罩和主药型罩的合理匹配，设计出来的新结构药型罩可达到减少前舱对射流干扰并提高侵彻威力的目的.

[1]HELD M.Transverse shaped charges[C].8th International Symposium on Ballistic.Orlando，USA：IBC，1984：39－47.

[2]HELD M，FISCHER R.Penetration theory of inclined and moving shaped charges [J].Propellants， Explosive，Pyrotechnics，1986，11（4）：115－122.

[3]XIAO Qiang－qiang，HUANG Zheng－xiang，ZU Xu－dong，et al.Supersonic penetration by jet into concrete：research of shaped charge for creating large cavity diameter [C].26th International Symposium on Ballistic.Miami，USA：IBC，2011：1 273－1 279.

[4]肖强强，黄正祥，顾晓辉.冲击波影响下的聚能射流侵彻扩孔方程[J].高压物理学报，2011，25（4）：333－338.XIAO Qiang－qiang，HUANG Zheng－xiang，GU Xiao－hui.Equation of penetration and crater growth by shaped charge jet under the influence of shock wave[J].Chinese Journal of High Pressure Physics，2011，25（4）：333－338.（in Chinese）

[5]HELD M.Verification of the equation for radial crater growth by shaped charge jet penetration[J].International Journal of Impact Engineering，1995，17（1）：387－398.

[6]HELD M，HUANG N S，CHANG C C.Determination of the crater radius as a function of time of a shaped charge jet that penetrates water[J].Propellants，Explosives，Pyrotechnics，1996，21（2）：64－69.

[7]GRADY D.Shock equation of state properties of concrete[C].International Conference on Structures Under Shock and Impact.Udine，Southamption：Computational Mechanics Publications，1996：1－10.

[8]HUERTA M，VIGIL M G.Design，analyses，and field test of a 0.7 m conical shaped charge[J].International Journal of Impact Engineering，2006，32（8）：1 201－1 213.

[9]Century Dynamic Ltd.Interactive non－linear dynamic analysis software theory manual[M].Ramon，USA：Century Dynamics Incorporated，2001.

[10]肖强强，黄正祥，顾晓辉.聚能装药侵彻混凝土的径向扩孔工程研究[J].兵工学报，2010，31（4）：464－468.XIAO Qiang－qiang，HUANG Zheng－xiang，GU Xiao－hui.Engineering research of radial crater growth for the penetration in concrete target by shaped charge jet[J].Acta Armamentarii，2010，31（4）：464－468.（in Chinese）