弹性导弹侧向动态特性分析

许兆庆，吴军基，薛晓中，孙 慧

（南京理工大学 能源与动力工程学院，南京210094；2.中国航天科技集团七院，成都610100）

巡航导弹是一种具有一定的盘旋滞空能力，能对目标区域进行实时侦察并精确打击高价值点目标和机动目标的导弹.由于其飞行高度低、速度低并需要很长的滞空时间，因而往往有大展弦比翼面，容易发生弹性振动，对其飞行稳定与制导精度产生影响.因而，有必要对弹性振动时导弹的动态特性做分析.随着速度的提高和减重愿望的增强，弹性飞行器的研究正成为热点，国内外学者在此领域做了大量的工作，在非定常气动力、结构稳定性、鲁棒控制等方面取得了不少成果[1，2].本文对某型巡航导弹在弹性振动时的侧向动态特性进行分析，计算了结构的固有模态，推导了弹性振动时的附加非定常气动力，建立了刚体扰动运动方程组，将弹性振动引起的附加非定常气动力作为干扰输入项，代入扰动运动方程组得出其响应，从而得到了弹性振动下的动态特性，为稳定性分析、精度分析及制导与控制系统的设计提供依据.

1 固有模态分析

弹体固有模态是动态特性分析的一项重要内容，包括计算结构的频率、振型等，这些参数与结构强度一样均属于结构的固有性质.它们不但能为弹体的气动弹性分析提供原始数据，也可为确定敏感元件在弹上的安放位置，进行控制系统的稳定性分析，预测导弹的振动环境以及确定弹上设备减振装置的频率特性等诸多方面提供数据.

使用MSC Patran创建有限元模型，模型网格划分如图1所示，忽略气动阻尼的作用；接着采用MSC Nastran软件进行巡航导弹的模态分析，计算结果第一阶振型如图2所示，一阶振动频率为22.8Hz，二阶振动频率为54.5Hz.

图1 结构模型网格图

图2 一阶弯曲振型图

由图2可见，导弹主要表现为翼面的振动，而弹体的变形则较微小.这是因为折叠翼的展弦比较大，相对刚度比较低，而弹体及尾舵的刚度相对比较大；而且弹体处于自由－自由的无约束状态，在垂直于弹体的载荷作用下弹体主要发生转动的刚体位移，而不是弹性挠动；折叠翼是自由－约束的悬臂梁状态，在垂直于翼面的载荷作用下将发生弹性挠动.翼面振动又主要为弯曲振动，扭转变形很小，这是由该翼的结构布局所决定的.该巡航导弹设计的飞行自由振荡频率为2 Hz，远低于结构一阶振动频率，因而不会产生共振.

2 非定常气动力

由结构模态计算可知，巡航导弹在飞行中主要表现为翼面的弯曲振动，因而也仅考虑弹翼的弯曲变形所产生的附加非定常气动力.为简化计算，假设只发生一阶弯曲振动.

弹性弹翼的任一片条在均匀风速流动中的动力学方程可采用简单振子的运动微分方程表示：

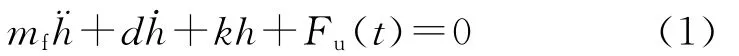
式中，h是片条的弹性位移，mf是片条的质量，d是与速度成正比的阻尼系数，k是弹性弹翼的刚度.Fu（t）为系统的附加非定常气动力，由非定常气动力理论可以假设Fu（t）＝F0h＋F1，其中，F0，F1为非定常气动力展开系数，其大小与来流动压有关[3]，代入方程（1）可以解得：h＝h0eλt，其中h0为初始位移，

从而Fu（t）＝（F0＋F1λ）h0eλt.根据片条理论，在整个翼上积分，则弹翼总的附加非定常气动力为

图3 弹翼弯曲挠曲线图

根据以上推导，附加非定常气动力整理后可以表示为FT（t）＝γ0Fye（ξ－iω）t，其中，Fy为不发生振动时总的升力值，γ0为非定常气动力系数；当忽略空气的阻尼作用时，ω近似为弹翼振动的固有频率.ξ为与结构刚度和来流动压有关的衰减系数，当ξ＜0时，非定常气动力逐渐衰减，为稳定的收敛状态；当ξ＝0时，非定常气动力维持等幅的振荡，为临界状态；当ξ＞0时，非定常气动力发散，为不稳定状态[3].

3 扰动运动方程组

本文所研究的巡航导弹主升力面为扇式折叠翼，采用3个格栅舵进行控制.格栅舵在舵机带动下绕图4所示的yd轴偏转，从而产生xd方向的阻力与zd方向的控制力；格栅舵受力分析如图5所示.

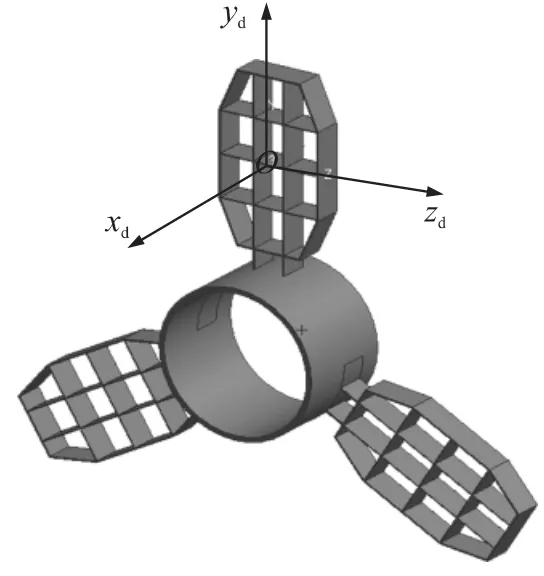
图4 格栅舵示意图

图5 格栅舵偏转受力分析图

在来流作用下由纵向翼肋与外框产生的法向力Fnδ可以分解为xd方向的阻力Fxδ与zd向的控制力Fzδ.假设弹体为刚体，不考虑地球曲率及科氏加速度等的影响，忽略高阶小量，不考虑质量变化，当攻角比较小时，忽略攻角对侧向的影响.采用文献[4]的坐标系统，巡航导弹侧向运动方程为

式中，F为推力，Fy为升力，Fz为侧向力，其余符号及其意义直接来源于文献[4].m为全弹总质量；v为速度；ωx，ωy，ωz为角 速度；Jx，Jy，Jz为 转动惯量；ϑ，α，β，γv，ψv，ψ，γ为各姿态角.

当进行侧向运动时，格栅舵按图6所示的方式偏转产生控制力，图示箭头为舵面控制力方向；舵的偏转情况为图6（a）和图6（b）的合成，以上舵面偏转作为基准.图6（a）中上舵面偏转与下舵面极性相反，大小为单个下舵面的2倍；2个下舵面偏转大小相等，极性相同.上舵面与2个下舵面对弹轴产生的倾斜力矩正好抵消，从而只提供偏航方向的力与力矩.图6（b）表示所有的舵面偏转都大小相等，极性相同，偏航力正好抵消，从而只提供倾斜力矩.如果考虑攻角的影响，则2个下舵面偏转角还需做略微的调整，以满足舵面控制力大小相等的要求.

图6 格栅舵偏转方式示意图

此时，计算特征点取为巡航飞行初始状态，飞行高度为海拔4 km，Ma＝0.8，飞行速度为259.5m/s，配平状态飞行攻角为1.5°，弹道倾角为0°，侧 滑 角 为 0°，全 弹 长1.8m，全 弹 总 质 量 为115kg.根据气动力计算，全弹压心至头部距离LB为0.862m；由结构计算，质心到头部距离LC为0.715m，舵距头部距离LδB取为1.75m，全弹计算参考面积Sw取弹体横截面积0.018 87m2，转动惯量Jx＝1.12kg·m2，Jy＝32.37kg·m2.

各力与力矩的线性化偏量为

式中，上标为对括号内的参数求偏导，如F（β）z为Fz对β求偏导；Δδy为偏航时图6（a）上舵面的偏转角，Δδx为倾斜时图6（b）上舵面的偏转角，以产生逆时针上舵面控制力为正.

侧向运动方程线性化并忽略小量后，将各参数值代入，则得到侧向扰动运动方程组[5]：

式中，Fgz，Mgx，Mgy分别为侧向干扰力、滚转和偏航干扰力矩.

4 弹性振动下动态响应

由扰动运动方程组可以解得干扰项与侧向速率和姿态角的传递函数.由于振动主要为弹翼的竖向弯曲，所以横向的Mgy与Fgz理论上可以不计.只需考虑绕弹体轴的滚转干扰力矩Mgx，此时传递函数为

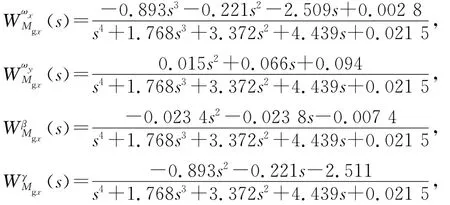
其中，上标参数表示传递函数的输出项，下标参数表示传递函数的输入项；左、右翼的振动可以假定频率与振幅都相同，而初相位却很难保证相同.当初相位相同时，Mgx＝0；当初相位差为π时，Mgx最大，为最不利情况，此时，

式中，FAL（t），FAR（t）分别为左、右翼面的附加非定常气动力，L0为翼面气动中心至弹体轴心的距离，为0.4m；单边翼升力Fy，W＝510 N；ω＝22.8×2π＝143.26rad/s.当ξ＞0时，气动与结构已经出现不稳定的发散，因而不必考虑此种情况；取稳定的最不利临界状态ξ＝0；考虑一般情况下附加非定常气动力初值在总升力的20%以内，因而可取γ0＝0.2，所以Mgx＝40.8（e－143.26it－e－143.26i（t－π/143.26）），通过传递函数可得此状态下姿态角偏量的响应，如图7、图8所示[6，7].

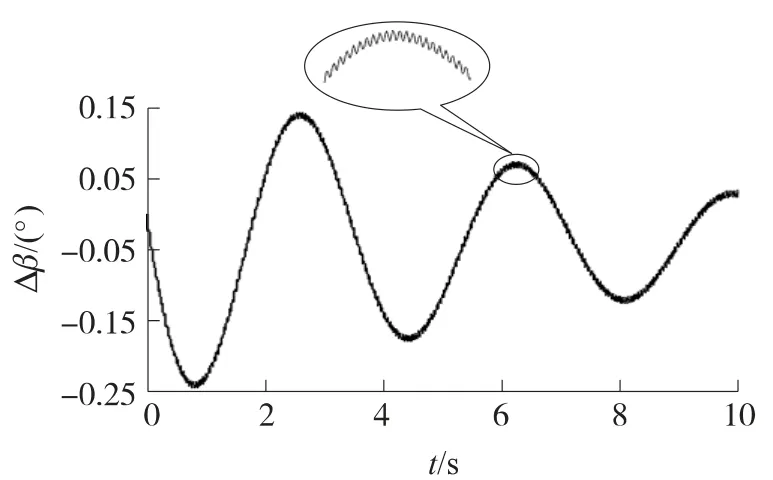
图7 Δβ响应图

图8 Δγ响应图

由图可见，在满足气动与结构稳定的前提下，侧滑角变化量仅在－0.25°～0.15°之间，并且随时间增长逐渐衰减；当左、右翼面振动相位差为π的最不利情况时，倾斜角的变化很明显，4s即可达到－14°，对飞行稳定造成不利影响，必须通过自动驾驶仪的控制作用来保持倾斜稳定.而且由图7上方的局部放大图可见，各姿态角都在做微幅高频振荡，振荡频率与弹翼振动频率ω一致，为22.8Hz，这将对弹上惯性器件等敏感设备的测量造成不利影响.因而在制导与控制回路设计时，必须考虑此因素，采用滤波等方式将振荡引起的高频信号消除.

5 结论

本文研究了大展弦比巡航导弹在弹性振动时的侧向动态特性，计算了结构的固有模态，根据对非定常气动力的研究与推导，得到了弹性振动下的附加非定常气动力表达式，将临界状态的附加非定常气动力作为干扰输入项代入扰动运动方程组，得到了弹性振动下各姿态角的动态响应.结果表明：①大展弦比弹性导弹主要为翼面的振动；②在满足气动与结构稳定的前提下，弹性振动引起的侧滑角偏量非常微小，当左、右翼面振动相位差为π时，倾斜角的变化很明显；③各姿态角都在做与弹翼一致的微幅高频振荡，对弹上惯性器件的测量将造成不利影响，必须设法消除此影响.

[1]杨超，许赟，谢长川.高超声速飞行器气动弹性力学研究综述[J].航空学报，2010，31（1）：1－11.YANG Chao，XU Yun，XIE Chang－chuan.Review of studies on aeroelasticity of hypersonic vehicles[J].Acta Aeronautica et Astronautica Sinica，2010，31（1）：1－11.（in Chinese）

[2]杨国伟.计算气动弹性若干研究进展[J].力学进展，2009，39（4）：406－419.YANG Guo－wei.Recent progress on computational aeroelasticity[J].Advances in Mechanics，2009，39（4）：406－419.（in Chinese）

[3]伏欣.气动弹性力学原理[M].上海：上海科学技术文献出版社，1982：32－275.FU Xing.Aeroelasticity mechanics principle[M].Shanghai：Shanghai Scientific and Technological Literature Press，1982：32－275.（in Chinese）

[4]钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2003：51－222.QIAN Xing－fang，LIN Rui－xiong，ZHAO Ya－nan.Missile flight mechanics[M].Beijing：Beijing Institute of Technology Press，2003：51－222.（in Chinese）

[5]张有济.战术导弹飞行力学设计[M].北京：宇航出版社，1998：90－218.ZHANG You－ji.Tactical missile flight mechanics design[M].Beijing：China Astronautic Publishing House，1998：90－218.（in Chinese）.

[6]卢学成，叶正寅.弹性飞行器大机动飞行气动特性分析[J].飞行力学，2010，28（2）：20－23.LU Xue－cheng，YE Zheng－yin.Analysis of aerodynamics characteristic of elastic aerocraft in maneuvering flight[J].Flight Dynamics，2010，28（2）：20－23.（in Chinese）.

[7]詹浩，程诗信，朱军.考虑气动弹性影响的机翼复杂气动外形设计研究[J].西北工业大学学报，2009，27（1）：100－104.ZHAN Hao，CHENG Shi－xin，ZHU Jun.An effective aero－dynamic and aeroelastic coupled design method for complicated wing shape[J].Journal of Northwestern Polytechnical University，2009，27（1）：100－104.（in Chinese）