磁阻传感器测量旋转弹滚转姿态的原理分析

马国梁，李 岩，葛敬飞

（1.南京理工大学 能源与动力工程学院，南京210094；2.中国人民解放军65651部队，辽宁 锦州121115）

弹箭类飞行器未加任何控制时对飞行姿态的测量问题涉及相对较少，而随着兵器发射理论与技术的发展，常规弹箭武器的制导化、灵巧化改造已成为各军事大国兵器领域的主流趋势之一.要想对弹箭飞行器施加控制策略，在构成整个闭环系统时往往需要测量反馈环节，姿态测量问题的重要性由此凸显.弹箭类飞行器常用的测量传感器主要包括：陀螺仪、加速度计、地磁传感器等.陀螺仪、加速度计等惯性器件被广泛应用于飞机和导弹的姿态测量中，在理论和技术上都已经发展到较高水平，但对制导弹药、灵巧弹药而言，由于很多时候仍采用常规发射平台，在应用惯性器件测量弹体飞行姿态时遇到了一些特有的困难，例如高过载、高量程、低成本、小体积等问题，使得惯性器件的应用受到限制.在地球磁场的作用下，地磁传感器能够反映出弹体飞行姿态的变化，因此地磁测姿技术得到了发展[1，2].地磁测姿具有成本较低、隐蔽性好、抗冲击能力强等优点.常用的地磁传感器主要包括线圈传感器、磁阻传感器、磁通门传感器等，其中磁阻传感器具有体积小、集成化等优点.

利用磁阻传感器测量高速旋转弹滚转姿态的方法在工程中已经得到实际应用.例如，弹道修正弹或者一些常规弹药往往采用地磁传感器测量弹丸的转速[3，4].常用的做法是将磁阻传感器安装在弹丸的径向平面内，其敏感轴垂直于弹体纵轴.国外有学者提出一些新的测量思路[5]，让其中一个磁阻传感器并不垂直于弹轴，即采用非正交安装的形式，这一方法在国内得到了进一步的研究[6].一些实验表明，在一定条件下用磁阻传感器测量旋转弹的滚转速率能保证一定的测量精度，而仅靠磁阻传感器测量滚转角有时会存在较大的测量误差，因此国内外学者研究了磁阻传感器与惯性传感器的组合测量滤波方法[7，8].

目前仅依靠磁阻传感器测量滚转角速率和滚转角的方法一般是假设在一个滚转周期内，俯仰姿态、偏航姿态保持不变或者变化很小，而姿态变化对转速和滚转角测量误差的影响在理论上仍缺乏更深入细致的分析.本文针对旋转弹的滚转姿态测量问题，研究了磁阻传感器的滚转姿态测量原理，并对测量误差的主要影响因素进行理论分析，分析结果通过数值仿真进行了验证.

1 磁阻传感器滚转角及磁阻传感器滚转角速率

滚转角速率的测量在原理上可以仅靠单个磁阻传感器来实现，有时为了确定弹丸的旋转方向或者为了提高测量性能，会在径向平面也就是外弹道学所说的赤道面内同时安装2个磁阻传感器.

假设一个传感器的敏感轴沿弹体坐标系yb轴方向，另一个传感器的敏感轴沿弹体坐标系zb轴方向，2个磁阻传感器所在赤道面的中心为Oh.地磁感应强度为B，在弹体纵轴方向上的分量为Bbx，在赤道面内的分量为Br，Br位于由弹体纵轴和地磁向量所决定的平面与赤道面的交线上，如图1所示.

Br在yb轴上的投影为Bby，在zb轴上的投影为Bbz.用B，Bbx，Bby，Bbz，Br分别表示相应向量的幅值大小，满足关系式：

为便于描述，在赤道面内定义zb轴与Br的夹角为磁阻传感器滚转角γm，弹底前视时，由zb轴逆时针转向Br为正，如图2所示.

图1 地磁向量分解示意图

图2 赤道面内磁阻传感器滚转角示意图

磁阻传感器滚转角γm为

将磁阻传感器滚转角γm随时间的变化率m定义为磁阻传感器滚转角速率.

旋转弹的射程不大时，可以认为地磁向量的大小和方向都保持不变，因此当弹体纵轴在地面坐标系下的指向不变时，地磁向量的径向分量Br的大小和方向都保持不变；相应地，Br在赤道面内的指向构成一条基准线，不随弹体旋转，只与地磁向量和弹体纵轴的指向有关.

以zb轴磁阻传感器为例，在弹体旋转过程中，zb轴随弹体一同旋转，当zb轴与Br的方向重合时，磁阻传感器滚转角γm＝0，zb轴磁阻传感器测得的磁感应强度达到极大值；当zb轴与Br的方向垂直时，zb轴磁阻传感器测得的磁感应强度为零.弹体转速基本恒定时，在一个滚转周期内，zb轴磁阻传感器的磁感应强度采样信号表现为正弦波，其周期正好对应磁阻传感器滚转角γm的变化周期Tm.

2 磁阻传感器滚转角速率测量原理

为了分析弹体姿态对磁阻传感器测量滚转姿态的影响，引入飞行力学中的姿态角概念：俯仰角ϑ，偏航角ψ，滚转角γ.用俯仰角ϑ和偏航角ψ可以确定弹体纵轴在地面发射坐标系下的指向.

2.1 磁阻传感器的测量方程

地磁感应强度向量B在地面发射坐标系中的三轴分量大小为Bx，By，Bz；弹箭飞行过程中Bx，By，Bz基本保持常值不变，可以在发射前进行测量标定.弹箭飞行过程中可以测得地磁感应强度向量B在弹体坐标系的三轴分量.根据飞行力学中的坐标转换关系可知，弹体坐标下各测量值分别为

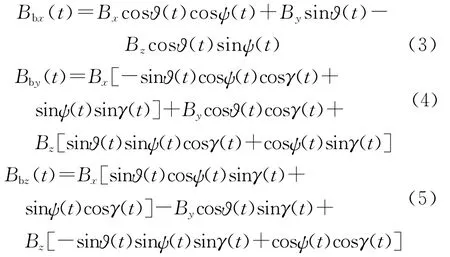
对于zb轴磁阻传感器，考虑采用“过零法”测量磁阻传感器滚转角周期Tm.假设在t时刻Bbz（t）＝0，形如式（5）所示，则此时zb轴与Br垂直.磁阻传感器滚转角经过π弧度的变化，在t＋0.5Tm时刻再次有Bbz（t＋0.5Tm）＝0.定义弹丸俯仰角速率（t），偏航角速率（t），滚转角速率（t），在t＋0.5Tm时刻的弹体姿态角分别为

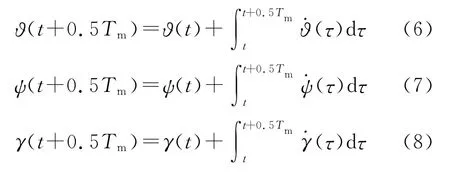
将式（6）～式（8）代入式（5），可以得到一个t＋0.5Tm时刻Bbz的测量方程.联合t时刻Bbz的测量方程，可以组成关于磁阻传感器滚转周期Tm及姿态角、姿态角速率的非线性积分方程组.要想由方程组求出Tm的解析表达式是非常困难的，甚至解析表达式根本不存在，为此需要转换分析思路.

2.2 磁阻传感器滚转角速率的测量方程

假定在一个磁滚转周期Tm内，磁阻传感器滚转角速率m变化很小，弹体转速较高时，这种假设很合理，即有m＝2π/Tm成立，由此可以分析弹体姿态变化对m的影响.根据式（2）进行求导运算，有：

再结合式（2）、式（4）、式（5）对式（9）进行整理化简，有：

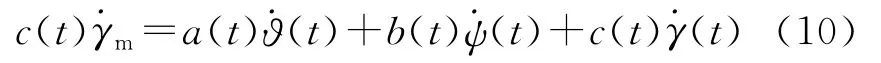
其中，

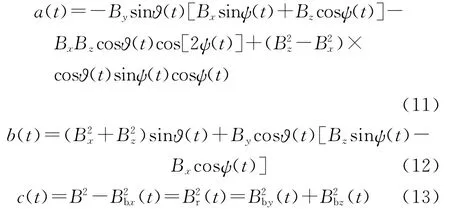
由式（13）可知，c（t）实际上是地磁向量在弹丸赤道面内的地磁分量幅值的平方.当地磁向量与弹轴不平行时，c（t）不为0，有

由式（14）可以得出如下分析结果：

①当（t）＝（t）＝0且c（t）≠0时，m＝，表明俯仰角速率、偏航角速率为零，且地磁向量与弹轴不平行时，磁阻传感器滚转角速率m与滚转角速率完全相等.

⑤当弹体纵轴与地磁向量之间的夹角较小甚至平行时，在赤道面内的地磁分量Br的幅值较小甚至为零，赤道面内磁阻传感器的测量值都较小.这种情况下由于磁阻传感器灵敏度的限制，将难以感知弹体的转动变化，造成测量盲区，也就不能用磁阻传感器测量滚转角速率.由于地磁向量一般在南北平面内，因此当沿着南北方向进行射击时，产生测量盲区的机率较大.

3 数值仿真计算

3.1 滚转角速率测量的数值仿真

以某火箭弹作为仿真对象，假定发射地点地理位置为东经118°，北纬32°，根据2010年发布的国际地磁模型数据，可得发射地点地磁向量的北向分量为3.303mT（向北为正），东向分量为－0.291mT（向东为正），地向分量为3.702mT（向下为正），可知地磁向量基本在南北平面内斜着向下，与水平面夹角约为－48.15°.

根据相关气动数据进行弹道仿真计算，俯仰角及偏航角的变化曲线如图3所示.为便于观察，分2个时间段进行绘图.

图3 俯仰角及偏航角曲线

可以看出，在开始的一段时间内，俯仰角和偏航角曲线波动较大，相应的俯仰角速率和偏航角速率较大，而在后期俯仰角和偏航角的变化曲线比较平滑，相应的俯仰角速率和偏航角速率较小.根据弹道计算结果，滚转角速率变化曲线如图4所示.

在弹丸赤道面内安装磁阻传感器，按式（9）对磁阻传感器滚转角速率进行计算.射向0°时，磁阻传感器滚转角速率m的变化曲线与非常一致.为便于观察，分2个时间段绘制出滚转角速率和磁阻传感器滚转角速率之间的误差－m的变化曲线，如图5所示.

可以看出，在开始的一段时间，由于俯仰角速率和偏航角速率较大，与m之间的误差较大，并随姿态角的波动而波动.在火箭弹飞行时间110s附近，弹轴与地磁向量的夹角达到极小，接近平行，使得误差－m出现局部极大值.

仅将射向调整为90°，其他弹道计算参数保持不变，沿东向射击后，分2个时间段绘制－m的曲线，如图6所示.

图4 射向为0°时磁阻传感器滚转角速率变化曲线

图5 射向0°时滚转角速率测量误差曲线

图6 射向90°时滚转角速率测量误差曲线

数值计算表明，利用磁阻传感器测量滚转角速率的最大相对误差在2种射向的情况下都没有超过7‰，这说明用磁阻传感器测量滚转角速率能取得一定的测量精度.

3.2 滚转角测量的数值仿真

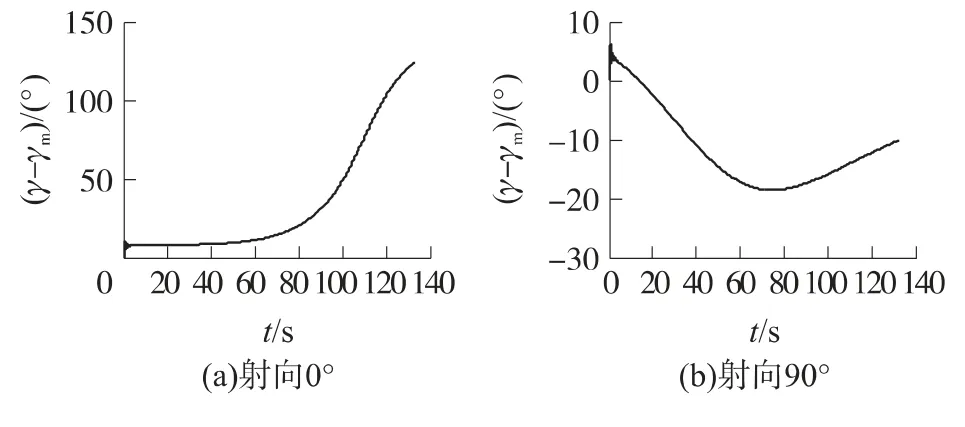
图7 滚转角测量误差曲线

射向90°时，在开始的一段时间内滚转角测量误差与射向0°时的变化范围比较接近，而在后期，滚转角速率测量误差一直较小，积分运算后，滚转角测量误差也远小于射向0°的情形，最大误差绝对值没有超过20°.

4 结论

利用磁阻传感器测量弹丸滚转姿态是一种较有工程应用价值的测量方法.本文深入分析了这一方法的测量原理，分析结果表明在径向平面内安装磁阻传感器时，测得的实际上是磁阻传感器滚转角速率，而弹体滚转角速率与磁阻传感器滚转角速率之间的测量误差受弹丸俯仰角、俯仰角速率、偏航角、偏航角速率、射向的影响.当俯仰角速率和偏航角速率为零且弹轴与地磁向量不平行时，磁阻传感器滚转角速率与滚转角速率完全相等.

数值仿真表明，用磁阻传感器测量滚转角速率的做法能达到一定精度，在工程上是比较可行的，而测量滚转角的做法实际上有很大的局限性，尤其是当弹丸沿南北向进行射击时，会存在很大的测量误差，在精度要求较高、弹丸飞行时间较长时，单独采用磁阻传感器测量滚转角的方法实际并不可行，需要结合其他姿态测量方法进一步深入研究.

[1]HARKINS T E，WILSON M J.Measuring in－flight angular motion with a low－cost magnetometer，ARL－TR－4244[R].2007：6－9.

[2]HARKINS T E.On the viability of magnetometer－based projectile orientation measurements，ARL－TR－4310[R].2007：5－10.

[3]沈波，黄晓毛，王志兴，等.基于地磁原理的计转数传感器技术研究[J].兵工学报，2003，24（3）：313－315.SHEN Bo，HUANG Xiao－mao，WANG Zhi－xing，et al.A study on a turns－counting sensor based on geomagnetism[J].Acta Armamentarii，2003，24（3）：313－315.（in Chinese）

[4]黄涛.弹丸转速的传感器测量方法[J].弹箭与制导学报，2002，22（4）：69－70，74.HUANG Tao.The method of measuring the projectile rotating speed with sensors[J].Journal of Projectiles，Rockets，Missiles and Guidance，2002，22（4）：69－70，74.（in Chinese）

[5]HEPNER D，HARKINS T.Determining inertial orientation of a spinning body with body－fixed sensors，ARL－TR－2313[R].2001：7－11.

[6]李玎，卜雄洙.基于非正交磁传感器组合的旋转弹体横滚角测试[J].兵工学报，2010，31（10）：1 316－1 321.LI Ding，BU Xiong－zhu.Roll angle measurement of spinning projectile based on non－orthogonal magnetic sensor[J].Acta Armamentarii，2010，31（10）：1 316－1 321.（in Chinese）

[7]LEE H，KIM K，PARK H，et al.Roll estimation of a smart munition using a magnetometer based on an unscented Kalman filter[C].AIAA Guidance，Navigation and Control Conference and Exhibit.Honolulu，Hawaii：AIAA，2008.

[8]李玎，卜雄洙，向超，等.基于磁/惯性传感器旋转弹体定姿的Kalman滤波器设计[J].中国惯性技术学报，2010，31（10）：76－80.LI Ding，BU Xiong－zhu，XIANG Chao，et al.Design of Kalman filter of attitude measurement of spinning projectile based on magnetic sensors and inertial sensors[J].Journal of Chinese Inertial Technology，2010，31（10）：76－80.（in Chinese）