可编程FIR 滤波器的FPGA 实现*

谢海霞，孙志雄

(琼州学院电子信息工程学院，海南 三亚572022)

随着信息技术、计算机和半导体集成电路的飞速发展，数字滤波器的理论与实现技术也获得极大的发展，并已经应用及渗透到许多重要学科和技术领域中。根据单位冲激响应函数的时域特性数字滤波器可分为IIR 滤波器和FIR 滤波器，其中FIR 滤波器是数字信号处理中常用部件，它的最大优点在于设计任何幅频特性时，可以具有严格的线性相位，这一点对数字信号的实时处理非常关键，因而受到人们的青睐［1－5］。

FIR 滤波器的设计实现大致有两种方法:一种是软件实现，使用高级语言如C/C++、MATLAB 等，在通用的计算机上实现，这种方法多用于教学或算法仿真，不能实现实时性。另一种是硬件实现，采用可编程逻辑器件(CPLD/FPGA)。FPGA 具有灵活的可编程逻辑，突破了并行处理与流水级数的限制，它所具有的查找表结构非常适用于实现实时快速可靠的FIR 滤波器，在加上Verilog HDL 语言灵活的描述方法以及与硬件无关的特点，使得使用Verilog HDL 语言基于FPGA 芯片实现FIR 滤波器成为研究方向［3］。本文对基于FPGA 的FIR 数字滤波器实现进行了研究，并设计一个16 阶的FIR 低通滤波器［6－10］。

1 FIR 滤波器的结构

FIR 有限脉冲响应滤波器是数字滤波器的一种，它的特点是单位脉冲响应是一个有限长序列，其数学表达式为:

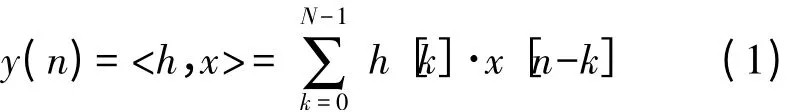
式中，N 表示FIR 滤波器的抽头数，y(n)表示第n 时刻的输出样本，h(k)表示FIR 滤波器的第k 级抽头系数，x(n－k)表示延时k 个抽头的输入信号。根据式(1)可得FIR 滤波器的直接型结构，如图1 所示。

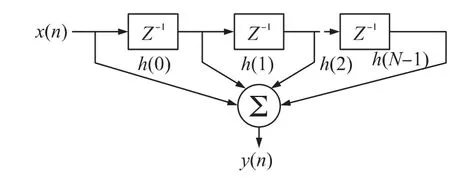
图1 直接型FIR 滤波器的结构示意图

用加法器和乘法器不难实现这种结构的FIR 滤波器，传给每个乘法器的操作数就是一个FIR 系数。所需乘法次数是N，加法次数是N－1。但这种直接实现的FIR 滤波器不论速度上还是资源耗用上都不理想。在使用FIR 滤波器的实际系统中，常常都会利用了FIR 滤波器的线性相位的新特点，因此根据线性相位FIR 滤波器的系数具有对称性这一特点，即h(n)=h(N－1－n)或h(n)= －h(N－1－n);因此，线性相位FIR 滤波器的直接型结构可改进为如图2 所示。

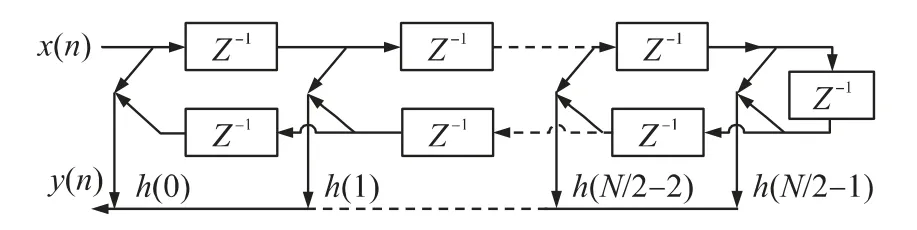
图2 线性相位FIR 滤波器的直接型结构改进图(N 为偶数)

在改进的结构中，N 次乘法减少为N/2 次，而加法次数增加了N/2 次，总的运算量得以减少。以乘法次数表示，其总运算量为N/2 次，这种直接型结构简单明了，系统调整方便［11－12］。

2 FIR 滤波器的抽头系数的MATLAB设计

2.1 FIR 滤波器的设计指标

本文设计的FIR 数字滤波器是低通滤波器，其设计指标为:采样频率是5 MHz，截止频率是1.5 MHz，输入、输出数据宽度是8 位，阶数是15 阶，通带衰减Ap=4 dB。

2.2 参数提取

使用MATLAB6.5 软件中Filter Design Toolbox工具箱中的FDATool，选择低通滤波器，Kaiser 窗设计方法，Fs=5 MHz，Fc=1.5 MHz，阶数为15 阶，线性相位。图3 是软件仿真结果图，如图3 所示，实线条是滤波器的幅频响应，频率为1.5 MHz 处幅频响应衰减Ap=4.8 dB，虚线条是相频响应，相频特性是线性，仿真结果满足设计指标要求。最后导出所设计的滤波器抽头系数，对其四舍五入处理后，16个抽头系数如下:

h［0］=h［15］=0.039 9;h［1］=h［14］=－0.014 5;h［2］=h［13］=－0.045 3;h［3］=h［12］=－0.056 0;h［4］=h［11］=0.027 0;h［5］=h［10］=－0.126 5;h［6］=h［9］=0.065 4;h［7］=h［8］=0.514 9。

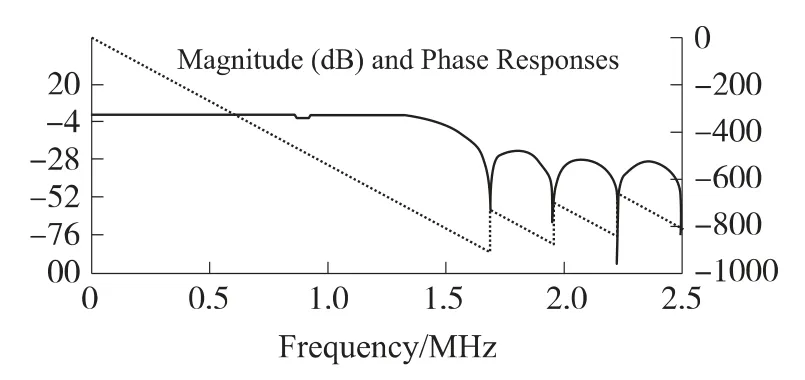
图3 FIR 数字低通滤波器频域特性图

3 抽头系数的最佳SD 编码

FIR 滤波器的抽头系数多为小数，且有符号，因此抽头系数的编码是必须考虑的一个问题。常用的编码方式有二进制补码、反码、有符号数值表示法等。

本例中采用以下的编码方式:将十进制数用2n数相加、减的形式表示出来，这种编码方法也被称SD(Signed Digit Numbers)编码，该编码与传统的二进制编码不同，它使用三个值来表示数字，即0、1、－1，其中－1 经常写为。例如:

2710=3210－410－12=1000SD(下标表示进制)

通常可以通过非零元素的数量来估计乘法的效率，比如乘法操作:A* x［n］，其具体实现过程如下。

若A10=(ak－1ak－2…a0)2，则

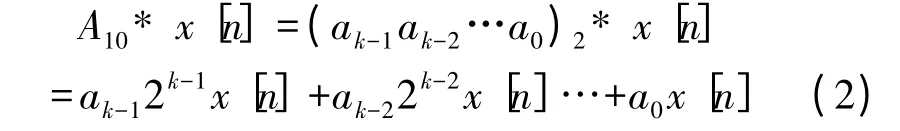
可以明显地看到，乘法的成本与A 中非零元素ak的数量有直接的关系。而普通二进制编码需要4 个加法器，用SD 编码只需要3 个加法器。

SD 编码通常不是唯一的，比如:

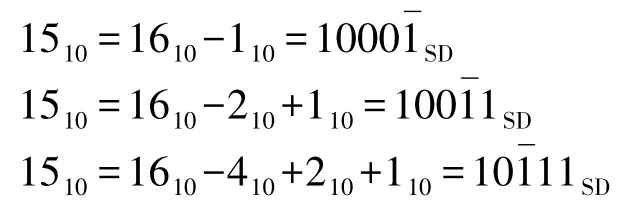
在上面的SD 编码中，由于第1 种方式具有最少数量的1 和，因此它的乘法成本最低，因此应该尽量减少编码中1 和的数量，以将乘法器实现的成本降低到最低，通常将这种包含最少1 和数量的SD 编码称为最佳SD 编码。

在滤波器系数的处理上，采用最佳SD 编码方式，以减少对器件资源的在耗用。滤波器系数的SD编码如下，每个抽头系数均先左移7 位(乘以128)。

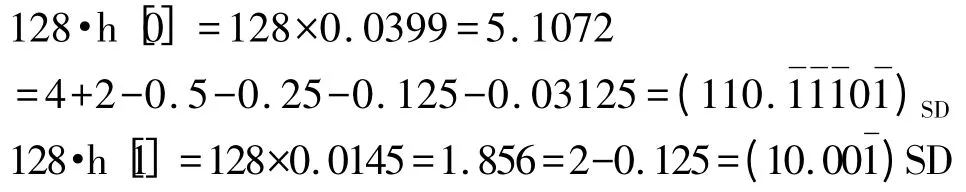
4 FIR 滤波器的FPGA 实现

FIR 滤波器采用对称结构，每个抽头的输出分别乘以相应加权的二进制值，再将结果相加。同时利用滤波器系数的偶对称特性，把输入信号x(n)进行以下等效:

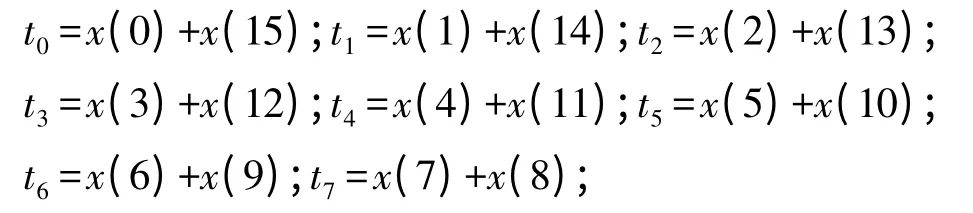
这样，16 阶FIR 滤波器的输出就可以用下面的算式得到:

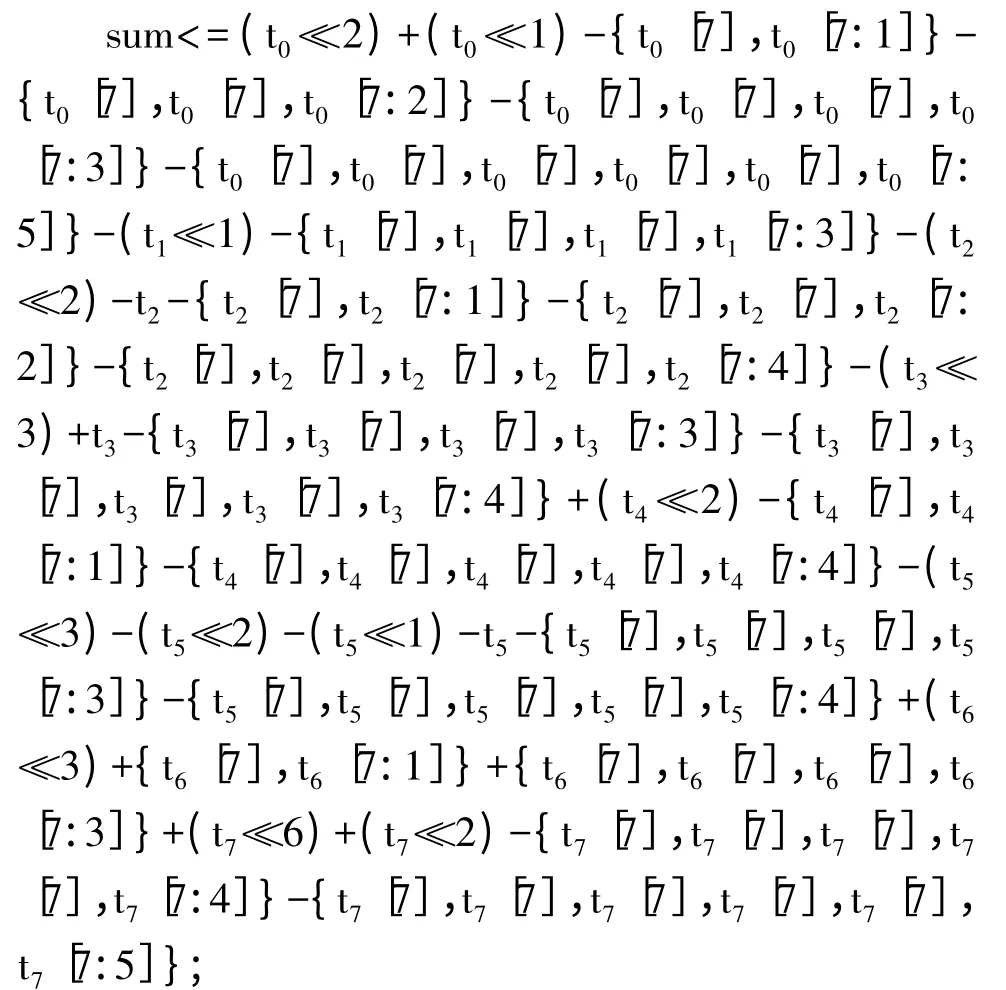
在得到结果后，再将结果右移7 位，即得到正确的结果。根据以上设计思路，用Verilog HDL 语言设计。仿真结果如图4 所示。

图4 16 阶FIR 滤波器的仿真结果

对QuartusⅡ仿真结果和MATLAB 计算的理论值进行比较分析，它们之间的误差如表1 所示。

表1 理论值与仿真结果

由上面仿真波形可以读出结果。经比较，仿真结果与输出信号理论吻合，除了一个38%的误差较大，其它的误差都在可接受范围内;且波形基本没有毛刺，设计符合要求。(部分比较大的误差出入是由于在设计中系数量化时引入的量化误差，以及舍位时产生的舍位误差，在数据比较小的时候。这种误差较为明显。)仿真结果正确后把生成的编程数据文件下载到FPGA 芯片中即可。

5 结束语

在实际使用的时候，大多数情况下，人们希望能够根据应用的不同场所改变滤波器的参数和性能，这就需要对滤波器的系数进行在线配置。本文设计的可编程滤波器能满足这一要求。可编程滤波器在数据处理上分为两个过程:第1 步完成滤波器系数的配置，将系数配置到抽头延迟线上;第2 步执行乘积和的计算，对乘积进行一位有符号扩展，并加到前面的部分乘积上。本文所介绍的设计、验证的方法都是可行的，具有很高的应用价值。

［1］ Shousheng He，Mats Torkelson.FPGA Implementation of FIR Filters Using Pipelined Bit－Serial Canonical Signed Digit Multipliers［J］.IEEE Custom Integrated Circuits Conference，1994(1－4 May):81－84.

［2］ 刘在爽，卢莹莹.高阶FIR 滤波器面向FPGA 的多种实现方法［J］.中国有线电视，2008(2):164－168.

［3］ 李莹，路卫军，于敦山. 一种在FPGA 上实现FIR 数字滤波器的资源优化算法［J］. 北京大学学报:自然科学版，2009，45(2);222－226.

［4］ 杨丽杰.基于FPGA 的FIR 滤波器设计方法的研究［J］. 东华大学学报，2006，(6):93－97.

［5］ 刘悦. FIR 数字滤波器的设计与实现［J］. 信息技术，2009，(2):8－9.

［6］ 江国强. EDA 技术与应用［M］. 北京:电子工业出版社，2006.1－15.［M］.清华大学出版社，2010.

［7］ 王金明，冷自强. EDA 技术与Verilog 设计［M］. 北京:科学出版社，2008.

［8］ 王道.CPLD/FPGA 可编程逻辑器件应用与开发［M］.北京:电子工业出版社，2004.

［9］ 冷邦明. 基于FPGA 的数字信号处理算法研究与高效实现［D］.哈尔滨工程大学，2009.

［10］ 朱霞，柴志雷，须文波. 基于FPGA 的数字滤波器乘法模块改进［J］.计算机仿真，2009，26(1):335－338.

［11］ 陈后金，薛健，胡健.数字信号处理［M］.第2 版.北京:高等教育出版社，2008.

［12］ 何宾.FPGA 数字信号处理实现原理及方法［M］.北京:清华大学出版社，2010.