直升机吊挂流场数值模拟与尾鳍设计分析

马 超 曹义华 徐忠达

(北京航空航天大学 航空科学与工程学院，北京100191)

直升机吊挂重物飞行是直升机飞行科目的重要内容之一.直升机吊挂飞行，不受到直升机机身容积、起飞地形环境等制约条件的限制，在战略物资运输、灾区快速援助、地质矿产勘探等方面有着广泛的应用.

国内外对直升机吊挂的研究主要集中于飞行过程中吊挂重物对直升机飞行动力学与飞行品质的影响.国外对直升机吊挂的飞行动力学与飞行品质问题研究开始较早，且已取得一系列研究成果［1－3］;国内近几年才相继开展相关方面的研究，也取得了一定的成果［4－5］.

在对直升机吊挂流场的研究中，国外多采用风洞实验与飞行试验的方法，着重考察吊挂物体自身绕流流场与稳定性问题.文献［6］在对直升机吊挂进行风洞实验过程中发现，在吊挂尾部安装尾鳍有利于吊挂的稳定性.文献［7］对UH-60黑鹰直升机吊挂进行了风洞实验，通过飞行试验对不同构型尾鳍的吊挂进行了稳定性分析.

本文采用计算流体力学(CFD，Computational Fluid Dynamics)方法，计算并考察了两种直升机吊挂构型的气动力与绕流流场特性，研究了吊挂尾鳍保证吊挂航向稳定性的作用机理.在忽略空气摩擦阻力的假设条件下，建立了吊挂摆动的运动方程，提出使摆动运动固有频率等于1的设计准则，利用该准则对第2种吊挂构型进行了尺寸设计.

1 第1种吊挂流场分析

本文计算的第1种吊挂构型被广泛用于直升机森林矿产勘探过程中，如图1所示.

图1 第1种直升机吊挂构型

该构型吊挂由外圈的发射装置与内圈的接收装置两部分组成，两者通过绳索绑定于同一平面，又通过绳索整体吊挂于直升机下方.发射装置和接收装置的外形几何尺寸为:吊挂外圈为发射装置，尺寸为外接于直径15 m圆的正十二边形圆管，圆管横截面直径为0.1 m;内圈为接收装置，尺寸为直径1 m的圆管，圆管横截面直径为0.15 m.

吊挂外圈边缘有一个保证吊挂航向稳定性的尾鳍，类似于飞行器中的垂直尾翼，根据图像初步测绘，可得尾鳍形状为直角梯形，根据飞行器垂直尾鳍的设计经验，选用NACA0012翼型为其横截面形状，测绘尺寸与三维实体模型见图2.

1.1 流场控制方程的求解

吊挂在运动过程中，流场的控制方程可以表示为下述通用形式:

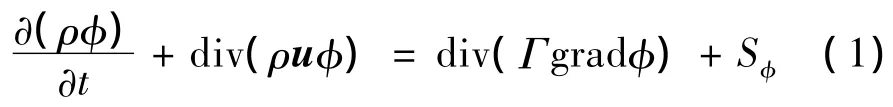
式中，φ为通用变量;ρ为空气密度;u为速度矢量;Γ为广义扩散系数;Sφ为广义源项.

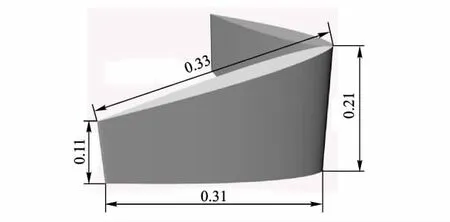
图2 尾鳍三维模型(单位:m)

CFD计算过程中，控制方程的离散基于有限体积法，对流项离散选用二阶迎风格式，采用计算不可压缩流动的SIMPLEC(Semi-Implicit Method for Pressure-Linked Equations Consistent)算法，通过压力场与速度场的反复求解与修正最终达到满足连续方程的需要.湍流模型采用S-A(Spalart-Allmaras)一方程模型.边界条件在吊挂表面选用无滑移的壁面边界条件，在外流场边界选用速度入口边界条件.

1.2 吊挂CFD计算结果

根据已有的吊挂尺寸数据，利用CAD软件建立吊挂三维实体模型，如图3所示.

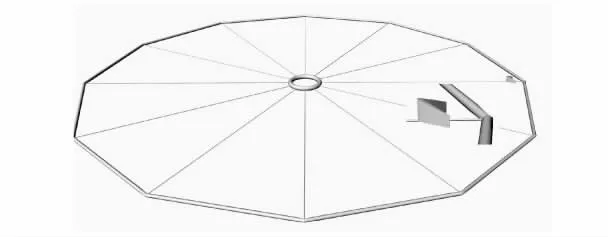
图3 第1种吊挂三维实体模型

在已建好的吊挂三维实体模型的基础上，对其进行离散网格划分，进而通过CFD计算整个吊挂的绕流流场.

根据直升机吊挂飞行的实际情况，计算条件中飞行速度为25 m/s，气压为标准大气压，计算得吊挂在运动过程中表面压力分布云图见图4.

从图4可以看出，吊挂表面压力分布与实际情况相符，来流方向表面静压较高.采用 NACA0012翼型的吊挂尾鳍产生的气动侧向力有效地保证了吊挂的航向稳定性.尾鳍位置的流场流线如图5所示.

从图5中可以看出，尾鳍对流场产生干扰，在侧滑角为0时尾鳍后缘位置会产生两个对称的低压涡，此时由于尾鳍的对称性，尾鳍产生的侧向气动力可以忽略.

1.3 吊挂理论计算结果

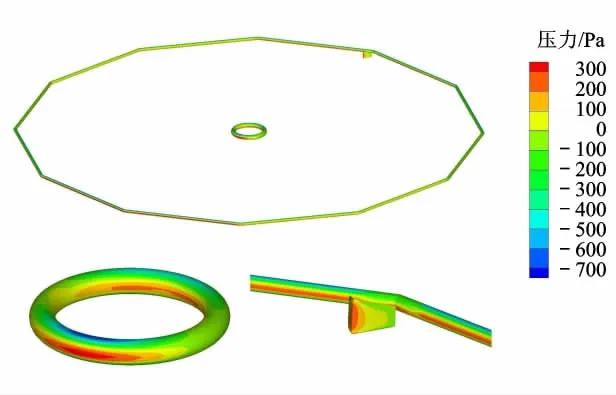
图4 第1种吊挂压力分布云图

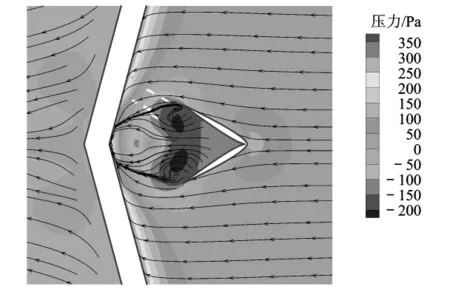
图5 第1种吊挂尾鳍流场流线图

第1种吊挂构型在运动过程中产生的气动阻力可以近似认为主要源自外圈发射装置12根圆柱体在空气中运动而产生的阻力.

文献［8］给出了圆柱体在空气中运动产生的气动阻力与流场雷诺数、圆柱表面的粗糙度之间的变化曲线.

在本算例中，根据计算条件可得流场雷诺数Re=2.58×105，在进行 CFD 计算过程中，圆柱表面不考虑粗糙度，按照光滑表面处理，因此，查表可得圆柱在该雷诺数下的基础阻力系数约为

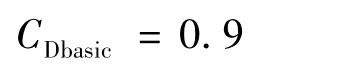
在真实运动过程中，由于吊挂构型的原因，12根圆柱体与来流存在不同的夹角.对于存在夹角的圆柱体，其阻力系数可根据文献［8］中公式求出:

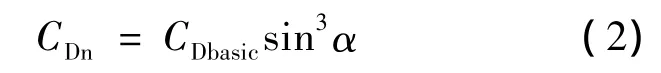
式中α为圆柱母线与来流方向的夹角.

综上，可以求得12根圆柱体在运动过程中产生的气动阻力，再通过气动力的计算公式，可以换算出整个吊挂的气动阻力系数CD=0.38.

1.4 计算结果对比分析

通过CFD与理论计算可以近似得到吊挂在运动过程中产生的气动力，由于吊挂主要为对称结构，在迎角为0的情况下，产生的气动升力可以忽略不计，因此本文仅比较两种计算结果的气动阻力系数，如表1所示.

表1 CFD计算与理论计算结果对比

从表1可以看出，CFD计算结果较理论计算结果偏小，主要是由于实际圆柱绕流中会产生比较严重的分离涡，而本文在CFD计算过程中，采用了工程应用较多的S-A一方程湍流模型，该湍流模型对于有大分离流动的流场模拟还存在一定的误差，因此，较理论计算结果会存在偏小的现象.

2 第2种吊挂流场分析

本文研究的第2种吊挂构型为一种常见的直升机矩形吊挂构型［9］，如图6所示.

图6 第2种直升机吊挂构型

文献［7］研究了不同尾鳍结构布局的矩形吊挂的稳定性问题，基于真实风洞实验数据与飞行试验数据得出的结论，研究吊挂对直升机稳定性的影响.根据其中对不同尾鳍结构布局的研究，本文选取了尾鳍角35°，安置于宽边偏上位置的构型，研究尾鳍对吊挂流场的影响.

矩形吊挂与尾鳍的尺寸数据可通过文献［7］得到，如图7所示.

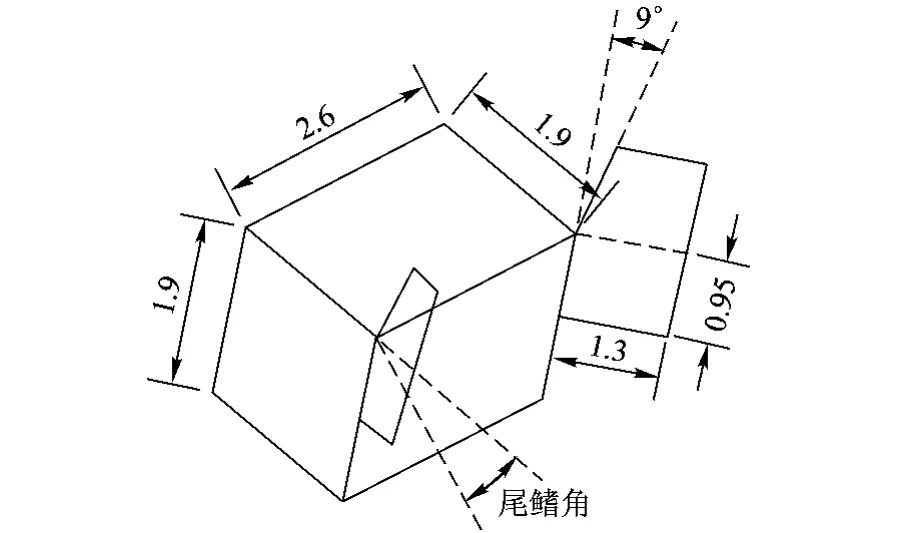
图7 矩形吊挂尺寸数据(单位:m)

相对于第1种吊挂构型，第2种构型的尾鳍明显较大，尾鳍对吊挂绕流流场的影响也更大，因此对于该构型，主要研究其绕流流场的特性.

利用上文提到的CFD计算方法，采用相同的算法步骤，计算条件根据文献选用飞行速度为20.5 m/s.可以得到绕流流场的流线图，见图8.

图8 矩形吊挂流线与压力云图

文献［9］利用CFD方法对矩形无尾鳍吊挂进行了计算，得到了无尾鳍的矩形吊挂绕流流场情况，见图9.

图9 文献［9］矩形吊挂CFD计算流线与压力云图

通过对比图8和图9，可以看出，本文计算的矩形吊挂压力分布与文献计算吻合较好，吊挂前缘存在高压分布区域，由于本文计算中尾鳍的存在，增加了矩形吊挂后缘处的低压区域，尾鳍后缘形成若干分离涡，由此产生的非对称气动力将对尾鳍的气动效率造成一定的负面影响.

3 尾鳍设计分析

尾鳍安装于直升机吊挂尾部，目的是保证吊挂的航向稳定性.如果在直升机飞行过程中吊挂受到了侧风影响，尾鳍会产生回复力矩保证吊挂能够及时地回复到平衡位置，进而保证直升机的稳定飞行.

3.1 前提假设

考虑吊挂尾鳍的作用机理，为了方便对尾鳍尺寸的设计研究，提出几点前提假设:

1)带有吊挂物的直升机飞行过程为悬停状态或匀速前飞状态;

2)将直升机吊挂作为刚体结构考虑，不考虑柔性变化;

3)直升机受到匀速侧风影响，且受到侧风时，假设吊挂仅在航向产生偏转，侧滑角定义为β，右侧滑为正方向;

4)直升机吊挂在受到侧风发生航向偏转过程中，忽略阻尼力即空气摩擦力的影响，摆动主要由惯性力与回复力共同作用产生.

3.2 设计准则

在忽略阻尼力的假设下，直升机吊挂受到侧风发生摆动时，运动方式应为简谐运动.运动中尾鳍的大小对吊挂航向稳定性有重要影响:如果尾鳍大，回复力矩就大，简谐运动的周期就短，吊挂会大摆幅、高频率地绕着平衡位置摆动，对直升机稳定性造成不利的影响;如果尾鳍小，回复力矩就小，简谐运动的周期就长，即抗侧风能力就差，回复速度慢，如果遇到连续侧风，有可能长时间不能回到平衡位置，也会对直升机稳定性造成不利的影响.

因此，考虑到吊挂摆动中尾鳍气动效率对直升机稳定性的重要作用，本文在尾鳍设计中，提出的设计准则为:将尾鳍尺寸设计为能够使得吊挂发生的简谐运动的固有频率ω0=1.

3.3 受力分析

根据上文提到的设计准则，需先建立吊挂摆动过程中的运动方程，进而确定吊挂摆动固有频率ω0的表达式.

吊挂在摆动过程中，如果忽略阻尼力，受到力的作用包括:

惯性力，由吊挂本身质量引起，当吊挂受到侧风偏离平衡位置时，其惯性力与侧滑角加速度有关，表达式为转动惯量I与侧滑角加速度的乘积，其中转动惯量I为矩形吊挂与尾鳍两者转动惯量之和，可根据吊挂与尾鳍质量与摆动半径确定.

回复力，由吊挂尾鳍产生的回复力矩引起，与尾鳍产生的气动侧向力、尾鳍气动中心到转动中心的距离有关.根据气动力的一般表达式，尾鳍产生的气动侧向力FW可表示为

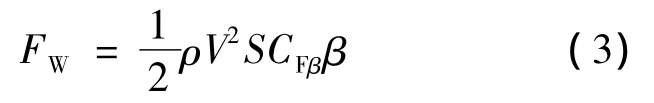
式中，V为空气来流速度;S为尾鳍面积;CFβ为尾鳍气动力系数随侧滑角β变化的斜率关系.

综上，吊挂在受到侧风做简谐运动时运动方程可以表示为

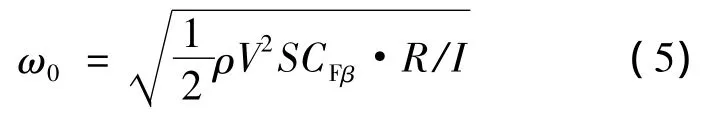
令ω0=1，即可求得尾鳍的尺寸参数.

3.4 讨论分析

根据式(5)，尾鳍尺寸与吊挂质量、飞行速度等参数有关.当吊挂质量确定时，飞行速度越大，尾鳍气动侧向力越大，尾鳍产生的回复力矩也变大，即尾鳍的回复效率高，有利于吊挂的稳定性，该结论与文献［7］中风洞实验结果一致.

以第2种吊挂构型为例，利用上文提到的尾鳍设计方法对该构型尾鳍进行设计.

首先应利用CFD方法计算尾鳍侧向气动力系数随侧滑角β变化的斜率关系CFβ.在计算条件中，加入5°侧滑角，其余计算条件不变，矩形吊挂流场流线图如图10所示.式中R为尾鳍气动中心到转动中心的距离.根据运动方程，摆动固有频率ω0的表达式为

图10 侧滑角情况下矩形吊挂流线与压力云图

通过CFD计算，5°侧滑角时尾鳍产生的气动侧向力FW=133.63 N，根据气动力计算公式可求得 CFβ=2.48 rad－1.

矩形吊挂质量由文献［7］查得为2 224 kg.假设矩形吊挂密度均匀分布，且尾鳍质量相对于吊挂物质量可以忽略不计，则矩形吊挂绕中心轴的转动惯量 I=1921.91 kg·m2.

按照构型尺寸，设尾鳍的气动中心在1/4弦长位置，则 R=1.22 m.

综上，通过式(5)，可求得尾鳍尺寸面积S=2.47 m2.而构型中尾鳍实际面积 S=2.4 m2，可知尾鳍实际面积略小于理论设计面积，则此时，尾鳍提供的回复力矩偏小，提高飞行速度能够有利于保证吊挂的稳定性，该结论与文献［7］中风洞实验结论一致.

4 结论

本文对两种直升机吊挂进行了CFD数值模拟计算，求出了吊挂的绕流流场，观察了吊挂的绕流流场特性.此外，研究了尾鳍对吊挂航向稳定性的影响机理，采用本文提出的尾鳍设计方法对第2种吊挂尾鳍进行了尺寸设计，定性结论与风洞实验结论一致，该方法在一定程度上能够满足工程设计的需要.

References)

［1］Cliff E，Bailey D.Dynamic stability of a translating vehicle with a simple sling load ［J］.Journal of Aircraft，1975(12):773 －777

［2］Nagabhushan B.Low-speed stability characteristics of a helicopter with a sling load［J］.Vertica，1985，9(4):345 －361

［3］Stuckey R A.Mathematical modeling of helicopter slung load［R］.DSTO-TR-1257，2001

［4］孙传伟，徐进.带大载荷吊挂直升机悬停纵向操纵性分析［J］.南京航空航天大学学报，2005，37(4):421 －425 Sun Chuanwei，Xu Jin.Longitudinal control characteristic analysis of heavy slung-load helicopter［J］.Journal of Nanjing University of Aeronautics and Astronautics，2005，37(4):421 － 425(in Chinese)

［5］崔利，曹义华，李国知.直升机吊挂飞行平衡、稳定性与操纵性研究［J］.航空动力学报，2010，25(10):2307 －2311 Cui Li，Cao Yihua，Li Guozhi.Studies on trims，stability，and controllability of helicopter with slung-load［J］.Journal of Aerospace Power，2010，25(10):2307 － 2311(in Chinese)

［6］Matheson N.The stability of portable bridges carried on slings beneath helicopter［M］.Melbourne，Victoria:Defense Technical Information Center，1980

［7］Raz R，Rosen A，Carmeli A，et al.Wind tunnel and flight evaluation of passive stabilization of a cargo container slung load ［J］.Journal of the American Helicopter Society，2010，55(3):032001-1－032001-18

［8］Hoerner S F.Fluid-dynamic drag:practical information on aerodynamic drag and hydrodynamic resistance［M］.NJ:Midland Park，1965

［9］Cicolani L S，da Silva J G A，Duque E P N，et al.Unsteady aerodynamic model of a cargo container for slung-load simulation［J］.The Aeronautical Journal，2004，108(1085):357 －368