泵控并联变量马达速度系统复合控制策略

郑 琦 李运华 杨丽曼

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

电液比例变量泵控并联变量马达系统是一种闭式结构的容积控制系统，具有调速范围大、传动平稳、抗污染和适应分布式负载等特点，已在重型车辆及工程机械和履带式装甲车等上得到广泛应用.由于该系统具有流量自适应分配特点和数学模型存在排量与压力和排量与角速度的相乘非线性环节，现有的数学模型和控制方案尚不能准确描述系统特征并获得满意控制效果.针对电液容积控制系统的相乘非线性问题，文献［1－3］采用了状态反馈精确线性化方法，并在其基础上设计滑模变结构控制律以提高系统鲁棒性，取得了良好的控制效果，但研究对象限于负载可测或小扰动系统.文献［4－5］提出了基于局部线性化的模型参考自适应控制，但未考虑变量机构的动态特性.

泵控并联马达系统是多变量系统，需协调多个调节变量间的关系.文献［1，4］通过维持回路期望流量平衡来协调泵和马达的排量，体现了“按需供给”的思想.考虑到马达的液压转矩为系统压力和排量的乘积，本文尝试通过变量泵对系统压力进行动态控制，使其与马达排量调节形成“合力”，改善系统动态性能.同时，在变量马达调速控制器设计中，引入扰动观测器，提高了其稳态性能.

1 基本描述

图1为变量泵控并联变量马达系统的闭式结构原理图.

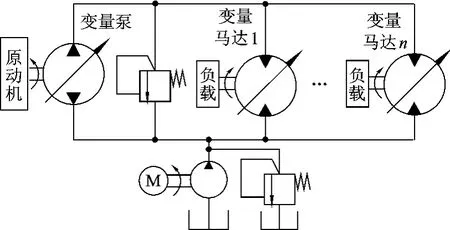
图1 并联变量马达系统结构原理图

泵控并联变量马达系统各环节数学模型［1］为

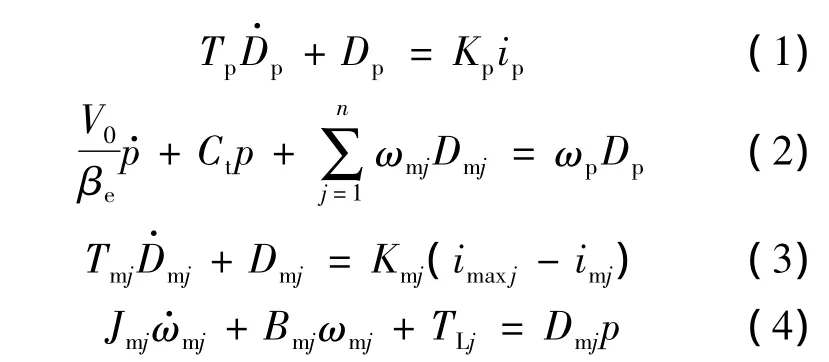
式中，Dp为变量泵排量;ip为变量泵变量机构控制电流;Tp为泵变量机构时间常数;Kp为泵变量机构电流-排量增益;p为泵两腔压力差;ωp为变量泵转速;V0为回路容积;βe为油液弹性模量;Ct为回路总体泄漏系数;j为系统中马达序号;Dmj为变量马达排量;ωmj为变量马达转速;imj为马达变量机构控制电流;imaxj为马达变量机构最大控制电流;Tmj为马达变量机构时间常数;Kmj为马达变量机构电流-排量增益;Jmj为归算至马达轴上的转动惯量;Bmj为马达轴上阻尼系数;TLj为马达轴上负载转矩.

本文采用变量泵控制系统压力，变量马达调节输出转速，通过各马达期望转速和实测转速的综合得到期望压力，系统架构规划如图2所示.

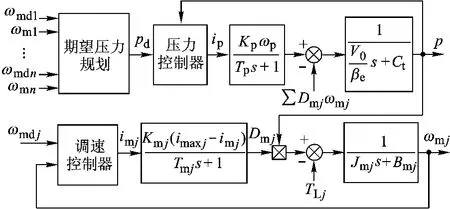
图2 泵控并联变量马达系统结构规划图

2 泵控压力系统设计

2.1 期望压力规划

通过系统压力的调节辅助马达排量调节，可使马达转速响应达到更好的动态效果.在泵控并联变量马达系统中，每个变量马达的运动状态均不同，需综合整体的响应情况.这里基于偏差控制思想对期望压力进行规划，规划算法如下:

式中，pbase为压力期望的基值，是系统稳定运行时的压力期望值，可依经验给定，此时维持系统压力稳定，可降低管路故障和泄漏污染;为压力期望的动态部分，综合各马达转速偏差而定，如此动态调节系统期望压力，可加快各马达的动态响应.其中，Kpd为单位转速偏差对应的系统期望压力动态值.

另外，需将压力期望的时间变化率约束在工程可实现且安全范围之内，即

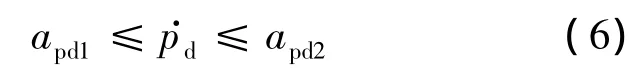
其中，apd1和apd2分别为的下限和上限，有apd1＜0，apd2＞0.

2.2 变量泵控压力系统模型线性化

由式(2)可得

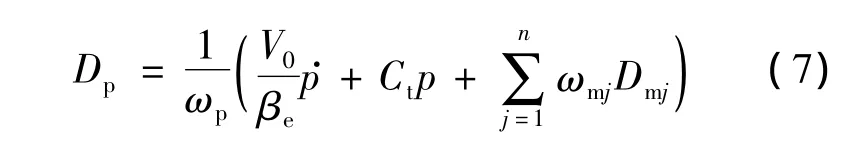
将式(7)代入式(1)，整理可得

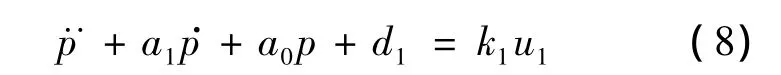
2.3 变量泵控压力系统滑模变结构控制

针对变量泵控压力系统，这里采用滑模变结构控制律设计控制器.定义跟踪误差为

构造滑模流型为

对式(11)求导，得

构造指数趋近律滑模控制器:

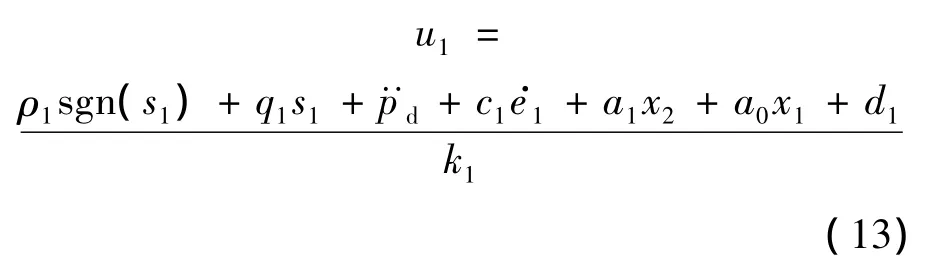
式中，q1＞0，ρ1＞0.将式(13)代入式(12)中，有

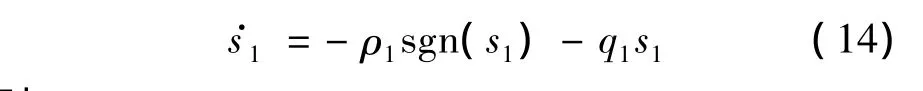
则

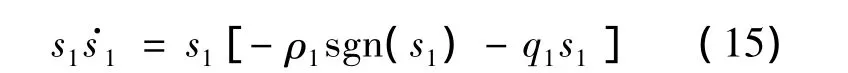
3 变量马达调速系统设计

3.1 变量马达调速系统模型线性化

对式(4)两边求导，可得

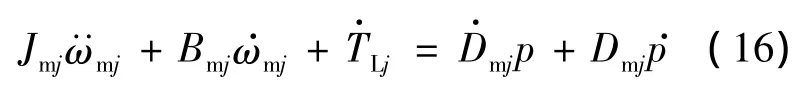
由式(3)可得

将式(17)代入式(16)，可得

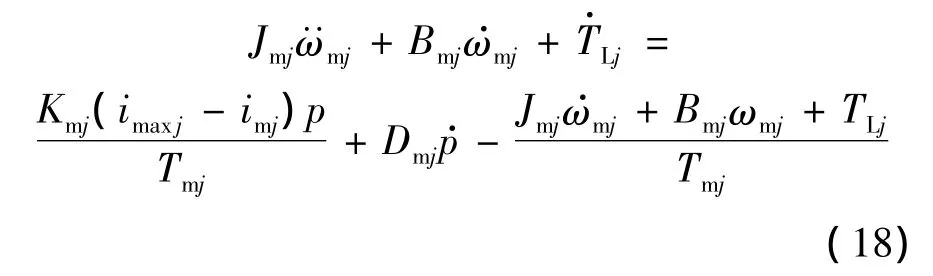
整理式(18)，可得

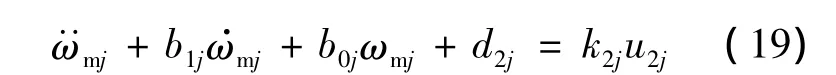
则其频域模型为

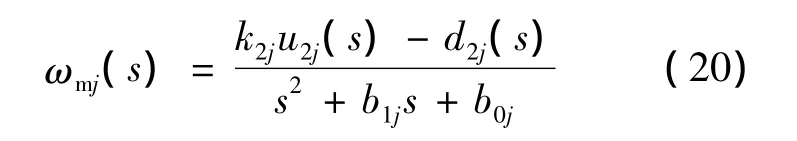
3.2 基于扰动观测器的变量马达调速控制

马达调速系统中的负载扰动主要由液压转矩克服.引入扰动观测器对扰动进行补偿，可有效提高系统的动态和稳态性能［6－9］.考察马达调速系统扰动项d2j，其不仅与未知负载转矩有关，还与系统压力波动有关.前文提出对系统压力进行动态调节，则必然引入扰动.为了克服上述两方面因素引起的扰动，采用文献［6］给出的方法设计扰动观测器，结构如图3所示.

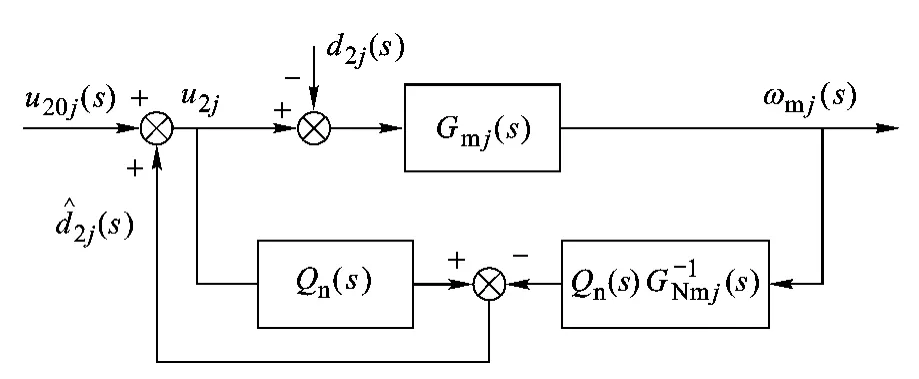
图3 扰动观测器结构图

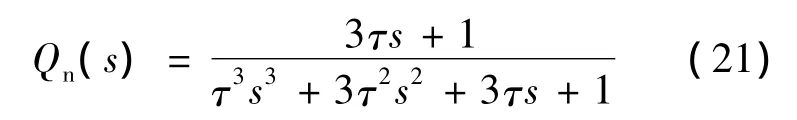
对于采用扰动补偿后的系统，采用PID(Proportion Integration Differentiation)控制器，则马达调速控制器形式为

可以看出，泵控压力控制器和马达调速控制器中仅涉及输出变量的一阶导数，实现时可采取卡尔曼滤波等方法对微分引起的干扰进行抑制［10－11］.

4 仿真分析

针对泵控并联双变量马达系统，对以下情况进行仿真:①在阶跃输入和冲击性负载下的响应;②波动压力条件下马达响应情况;③动态调节系统压力对系统动态性能的影响.

4.1 系统阶跃响应

马达1，2在0 s时刻分别给定阶跃转速信号ωd1=300rad/s，ωd2=200rad/s，施加负载为 TL1=TL2=60N·m，并在3.5s时刻将马达1负载突加至TL1=80 N·m.图4为双变量马达转速响应，图5为系统压力响应.如图4所示，马达转速的动态响应迅速，且基本无静差.马达1在3.5 s时刻的冲击负载扰动下，很快调整回期望转速，此过程对马达2基本没有影响.从图5中可以看出:当阶跃信号给定时，系统压力期望迅速增大;当整体转速偏差减小，期望压力随即减小，并稳定于pbase.动态调节过程中，压力的变化速率被约束在允许范围之内.

图4 双马达转速阶跃响应

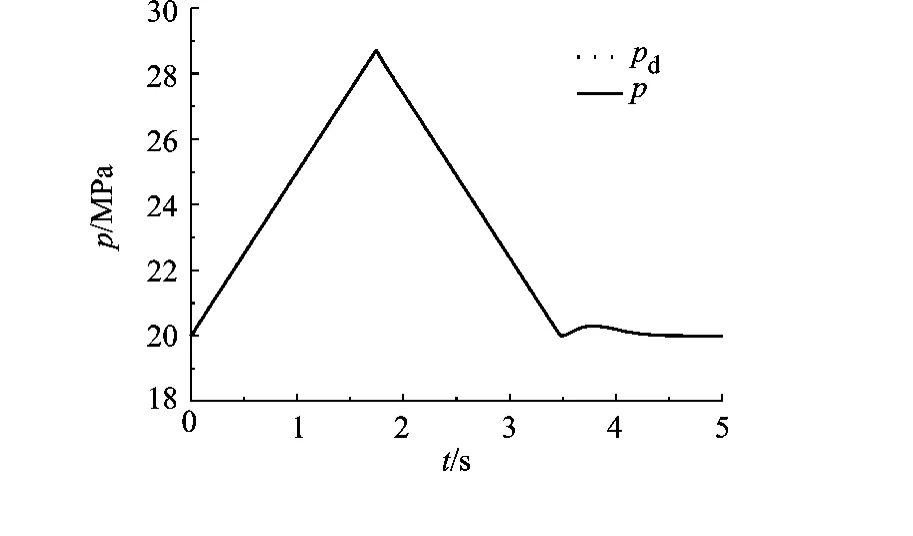
图5 系统压力响应

4.2 压力波动情况下马达响应

在压力控制给定端设置频率为2 Hz，动态幅值为5 MPa的正弦信号，补偿前后的压力波动和转速控制效果的比较如图6所示.从图6中可以看出:有扰动补偿时马达转速响应很好的趋近并稳定于期望转速，基本不受到系统压力波动影响;无扰动补偿时，转速能接近期望值，但随压力变化而波动，且有稳态误差.这说明基于变量马达线性化模型的非线性控制方法是可行的，扰动观测器的引入提高了系统抗扰动能力.

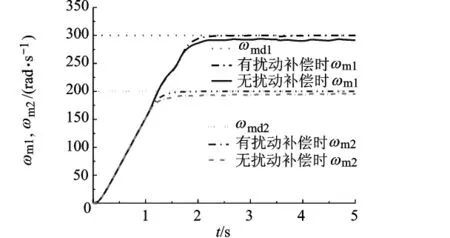
图6 波动压力下双马达转速响应

4.3 动态调节系统压力与恒压状态下的对比

分别在恒压25 MPa下、动态调节系统压力条件下和恒压20 MPa下考察阶跃转速响应.图7中动态压力调节与恒压25 MPa下马达1动态响应速度几乎一致，较恒压20 MPa下的调节时间缩短45%.转速进入稳态后，压力为基值20 MPa，油液泄露流量Qc接近于恒压20 MPa时，较25 MPa时减少20%，如图8所示.因此，该方案在保证性能的前提下，可有效地减少油液泄露，改善了工况环境，提高了系统可靠性.

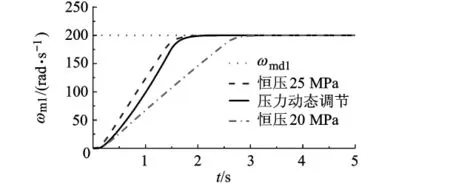
图7 不同压力条件下马达1转速响应

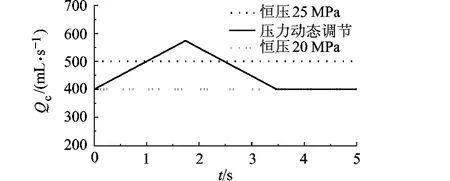
图8 不同压力条件下油液泄漏流量曲线

5 结论

1)所提出的泵控压力系统和变量马达调速系统的泵控并联马达系统的总体架构能够综合多个控制变量间的协调关系，并减弱马达间耦合.

2)所提出的综合多马达转速偏差的期望压力规划方法可以提高马达转速响应的动态性能，同时降低系统压力波动.

3)在马达调速控制器引入扰动观测器可以有效地提高抗扰能力和稳态精度.所提出的复合控制策略在结构上较基于精确线性化的方案更为简单，且较易于实现.

References)

［1］王岩.变量泵控制变量马达系统变结构控制算法［J］.北京航空航天大学学报，2010，36(12):1453－1456 Wang Yan.Variable structure control for variable pump controlling variable motor［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(12):1453 －1456(in Chinese)

［2］白国长，祁晓野，王占林.具有相乘非线性的马达速度鲁棒控制［J］.北京航空航天大学学报，2008，34(7):803 －806 Bai Guochang，Qi Xiaoye，Wang Zhanlin.Motor speed robust control with multiplying nonlinear property［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(7):803 －806(in Chinese)

［3］郎燕，李运华.电液复合调节作动器的精确线性化建模与控制［J］.北京航空航天大学学报，2009，35(9):1062 －1066 Lang Yan，Li Yunhua.Exact linearization based modeling and control for electro-hydraulic compound regulating integrated actuator［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(9):1062 －1066(in Chinese)

［4］王岩，付永领，牛建军.变量泵-变量马达自适应控制算法研究［J］.中国机械工程，2009，20(10):1173 －1179 Wang Yan，Fu Yongling，Niu Jianjun.Adaptive control algorithm for variable pump variable motor system［J］.China Mechanical Engineering，2009，20(10):1173 －1179(in Chinese)

［5］马鹏飞.全液压推土机液压行驶驱动系统动力学研究［D］.西安:长安大学工程机械学院，2006 Ma Pengfei.Study on hydraulic bulldozers moving hydraulic driving system dynamics［D］.Xi’an:School of Construction Machinery，Chang’an University，2006(in Chinese)

［6］Kempf C J，Kobayashi S.Disturbance observer and feedforward design for a high-speed direct-drive positioning table［J］.IEEE Transactions on Control Systems Technology，1999，7(5):513 －526

［7］White M T，Tomizuka M，Smith C.Improved track following in magnetic disk drives using a disturbance observer［J］.IEEE/ASME Transactions on Mechatronics，2000，5(1):3 －11

［8］Shim H，Jo N H，Son Y.A new disturbance observer for non-minimum phase linear systems［C］//Proceedings of the 2008 American Control Conference.Washington:IEEE，2008:3385 －3389

［9］Chang J L.Applying discrete-time proportional integral observers for state and disturbance estimations［J］.IEEE Transactions on Automatic Control，2006，51(5):814 －818

［10］Kobayashi K，Cheok K C，Watanabe K.Estimation of absolute vehicle speed using fuzzy logic rule-based Kalman filter［C］//Proceedings of the 1995 American Control Conference.Evanston:The American Automatic Control Council，1995:3086 －3090

［11］Cuibus M，Bostan V，Ambrosii S，et al.Luenberger，Kalman and neural network observers for sensorless induction motor control［C］//Proceedings of the Third International Power Electronics and Motion Control Conference.Beijing:International Academic Publishers，2000:1256 －1261