径向复合功率合成超声振动系统*

刘世清， 王家涛， 苏 超， 朱天宇， 王娉婷， 董 飞

(浙江师范大学应用声学研究所，浙江金华 321004)

0 引言

超声振动系统是超声拉丝、冷拉管等金属成型设备的核心部件，由于单个超声换能器的功率容量有限，人们常采用大功率超声合成系统［1-3］．20世纪60年代，美国Aeroprojects公司开发出了一种用于工业化生产的大功率超声冷拔金属管系统;我国20世纪80年代由中国科学院与上海钢管厂联合研制出一种冷拔钢管功率超声合成器．目前工程应用中的功率合成振动系统主要有2种［4-5］：一种是L-L型功率超声合成系统，该系统采用一组纵向换能器联合激励一根波导杆的纵向振动来获得大功率输出;另一种是R-L型及L-L-L型正交耦合振动方向变换器．如R-L系统由圆盘和通过盘中心并与之正交联接的杆构成，利用盘杆之间的振动耦合将盘的径向振动变换为杆的纵向振动获得大功率输出．

上述功率合成系统的特点均通过振动合成来获得大功率纵向振动能量输出．本文以纵向压电超声换能器与变厚度剖面圆盘构成的径向复合型功率合成超声振动系统为对象进行研究．该系统通过1组纵向压电超声换能器对圆盘进行径向激励，可获得大功率径向振动能量输出，并可直接作用于拉管系统的环形拉模上，提高拉模效率．采用谐振叠加法设计了功率合成振动系统．基于机电类比原理，建立了复合系统的变厚度剖面圆盘径向振动机电等效图，得到其频率方程，并进行了有限元仿真计算分析．通过实验测试了功率合成系统的共振频率，理论与实验结果吻合．

1 纵-径耦合型功率合成振动系统分析

图1为径向复合型功率合成超声振动系统．为提高系统的位移振幅放大系数及能量传输效率，系统采用1组纵向复合压电超声换能器与楔形剖面圆盘径向复合而成，构成由外向内的聚能系统．该系统的圆盘作为变幅起阻抗变换及振幅放大作用．事实上，该圆盘可直接作为拉模进行设计．换能器沿圆盘周向对称分布，并对盘作径向激励，在圆盘内表面可获得大功率径向振动能量输出．若压电换能器径向激励频率与圆盘径向共振频率一致，整个系统即处于共振状态．此时可采用谐振叠加法对系统各部分进行单独设计．由于压电换能器是一个机电耦合系统，通常采用等效电路进行设计．作为纵向复合压电超声换能器，其设计理论已比较成熟．因此，圆盘的径向振动是本文的重点研究对象．采用机电类比原理建立楔形剖面圆盘径向振动机电类比电路，进而得出其径向共振频率方程，并对其径向振动特性进行分析．

2 楔形剖面圆盘径向振动分析

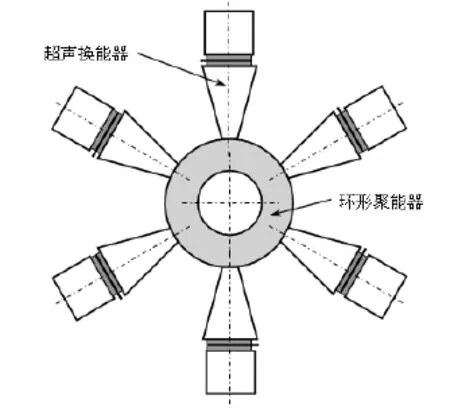
图1 径向复合功率合成超声振动系统

考虑径厚比较大的楔形剖面薄圆盘，其内沿厚度小于外沿厚度，构成由外向内的聚能变幅器，利用换能器激励可获得较大内外表面径向位移振幅比，如图2所示．其内外半径分别为b，a．在满足薄盘条件情况下，其厚度方向振动可忽略，而只考虑其半径方向的振动．不计径厚耦合，薄圆盘的纯径向振动为一平面应力问题．柱坐标系中任意变等厚度盘轴对称径向振动微分方程为［6］

图2 楔形剖面圆盘径向振动分析示意图

式(1)中：ξr为径向振动位移;t(r)为楔形剖面变化函数;ρ为材料密度;ν为材料泊松比;E为材料弹性模量．盘中径向正应力为

设楔形剖面厚度变化函数为t(r)=δr，δ为厚度变化因子．由式(1)得

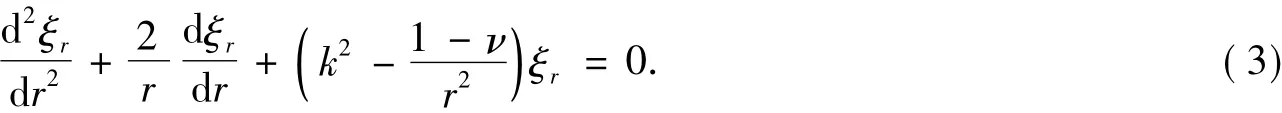
式(2)中：k为纵波波数;k=ω/c;c=［E/ρ(1－ν2)］1/2为径向振动波速．由波动方程(3)，并考虑到圆盘做纯径向简谐振动，通解可表示为

2．1 位移振幅放大系数

位移节点(节面)及振幅放大系数是变幅器的2个重要参数．设楔形剖面变幅器内、外侧面处质点位移振幅分别为 ξ1，ξ2．自由边界条件为

由式(4)、式(6)得 C1，C2的表达式为：

令 F(kb)=F(kr)，G(kb)=G(kr)，则上式中

将待定常数C1，C2表达式代人式(4)，得楔形剖面盘的径向位移分布函数表达式为

当位移为零时，由式(11)得位移节圆方程为

设r=a，ξr=－ξ2，定义振幅放大系数为内、外侧面质点位移振幅之比，由式(11)得位移振幅放大系数表达式为

对给定的几何尺寸，通过频率方程求得变幅器的共振频率，即可由式(13)求得变幅器的位移振幅放大系数．

2．2 机电类比等效电路

以F1，F2，v1，v2分别表示变幅器内外辐射面处的外力及质点振速，当 r=b时，v=v1;r=a时，v= －v2．由此得 C1，C2的表达式为：

将式(14)及式(15)代入式(2)得

由一般边界条件，Fr|r=b=Tr|r=b·Sb= － F1，以及 Fr|r=a=Tr|r=a·Sa= － F2，得：

式(7)～式(8)中，z01=ρcS1与z02=ρcS2分别表示盘形变幅器内、外侧面特性力阻抗．其中S1=2πbt(b)，S2=2πat(a)分别表示盘形变幅器内外侧面积．式(17)、式(18)可进一步整理为如下形式：

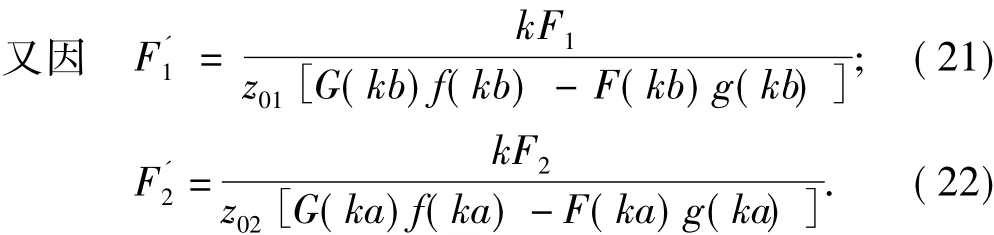
依据四端网络理论，式(19)、式(20)可用如图3所示的T型等效电路来描述．图3中各臂机械阻抗分别为：

图3 楔形剖面圆盘径向振动等效电路图

2．3 频率方程

对于自由径向振动楔形剖面圆盘，由等效电路图3可得其外侧面机械输入阻抗为

将上述各机械阻抗z1，z2，z3的表达式代入式(26)，并由机械共振条件Im(zi)=0，化简可得圆盘径向共振频率方程为

显然，径向共振频率方程(27)为一个含有非整数阶第一类和第二类Bessel函数的复杂超越方程，借助计算机可求出相应的径向共振频率的数值解．

3 算例

应用中通常采用钢和硬铝作为变幅器材料．以下对圆盘在第1、第2阶径向共振状态下，其振幅放大系数及频率特性进行理论及有限元分析．材料特性参数分别为：钢：ρ=7 800 kg/m3，ν=0．28，E=209 GPa;硬铝：ρ=2 790 kg/m3，ν =0．34，E=71．5 GPa;圆盘的几何参数取外半径 a=50 mm，外沿厚度t(a)=10 mm，内沿厚度t(b)=6 mm．为简化计算，引入半径比γ=b/a．以γ为变量对楔形剖面圆盘的位移振幅放大系数及其第1、第2阶径向共振频率进行了数值和有限元仿真计算．理论与仿真结果如图4～图6所示．

图4为钢制楔形剖面盘基频及第2阶径向共振位移振幅放大系数与其内外半径比的关系．图中M1，M2分别表示第1、第2阶振幅放大系数．由图4可见，振幅放大系数存在一个极大值．对于基频共振模态，此极大值对应的半径比γ≈0．4;而第2阶共振模态，该极大值对应的比γ≈0．15．显然，基频共振时振幅放大作用不明显，特别当圆盘的γ＜0．2时，M1＜1，圆盘不构成由外向内的变幅器，这在设计中必须注意的问题．而第2阶共振模式具有显著的位移振幅放大系数，理论与有限元仿真结果一致．此外，从图4可以看出，当圆盘γ趋于1时，M1，M2均趋于1，即无振幅放大作用．事实上，当γ→1，即薄壁极限圆环，其内外侧面振幅一致．在超声工程应用领域，变幅器位移振幅放大系数越大越好．就振幅放大系数而言，第2阶共振较好．

图4 第1、第2阶径向共振幅位移振幅放大系数与半径比关系

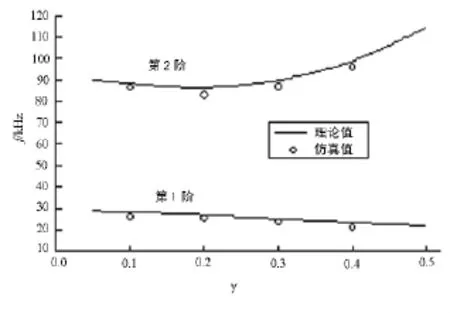
图5 第1、第2阶径向共振频率与半径比关系

图5 为楔形剖面圆盘形变幅器的第1、第2阶径向共振频率与其内外半径比之间的关系．由图5可见，圆盘振子的基频随其γ增大而单调下降．而第2阶共振频率开始随γ增大略有降低，当γ达到一定值时，共振频率随γ增大单调上升．原因是第2阶径向共振模式时，盘中出现了一位移节圆．当变幅器内外半径比增大时，其环宽变小，相当于谐振“长度”变短，因而频率升高，理论与仿真结果一致．进一步分析表明，当圆盘振子的γ→1，即b→a时，其第2阶径向共振频率为无穷大．因而对薄壁圆环振子只存在径向基波，而无高次谐波．

图6为相同几何尺寸的钢制和铝制圆环基频共振位移振幅放大系数随其半径比的变化关系．由图6可知，铝制圆盘振子的振幅放大系数高于钢制圆盘．此外，铝制圆盘的M1极大值对应的γ值小于钢制圆盘．

图6 钢、铝制圆盘基频振幅放大系数与半径比关系

4 实验

系统采用各组件单独设计的方法，加工了6个聚能型纵向复合压电超声换能器，理论设计频率均为30 kHz，实测谐振频率分别为 29．783，29．907，29．928，29．952，30．041 及 30．173 kHz．金属圆盘材料选用45号钢，几何尺寸为：外径80 mm，内径30 mm，外沿厚度10 mm，内沿厚度6 mm．其剖面为楔形．由频率方程(27)，算得圆盘第1阶径向共振频率的理论值为29．791 kHz．组装后的功率合成超声振动系统如图7所示．

6个纵振换能器之间以电并联方式连接，在小信号下测试，利用PV70A阻抗分析仪测得该功率合成超声振动系统的共振频率为29．536 kHz，系统共振频率与各组件共振频率吻合较好．

图7 试验样品

5 结论

1)本文对纵-径耦合型功率合成超声振动系统进行了研究．基于机电类比原理，导出了系统的楔形剖面圆盘变幅器径向振动等效电路及频率方程，并得到了其位移振幅放大系数的表达式．

2)理论及有限元仿真结果表明，存在一最佳半径比，使得盘形变幅器振幅放大系数达极大值．该极大值对应的半径比与材料特性及振动模式有关．对于盘形变幅器，其基频振动模式振幅放大系数较小，要获得较大的振幅放大系数，除选择合适的材料及半径比外，采用第2阶径向共振模式较好．

3)采用谐振叠加法设计了功率合成系统，并对其共振频率进行了测试，结果表明，理论与实验吻合较好，相对误差小于3%，满足工程应用需要，为超声振动拉模系统的设计提供了参考．

［1］Siegert K．Uner J．Superimposing ultrasonic waves on the dies in tube and wire drawing［J］．Journal of Engineering Material and Technology，2001，123(4)：517-523．

［2］谢涛，齐海群，张俊．超声振动拉丝实验研究［J］．中国机械工程，2006，17(3)：224-226．

［3］刘迟斌．超声波振动拉管系统的失谐补偿研究［J］．塑性工程学报，2004，11(6)：89-92．

［4］王爱玲，祝锡晶，吴秀玲．功率超声振动加工技术［M］．北京：国防工业出版社，2007．

［5］苏敦珍．超声冷拔钢管［J］．钢管技术，1985(1)：21-23．

［6］Gladwell G M L．The vibration of mechanical resonators(II)［J］．Journal of Sound and Vibration，1967，6(3)：351-64．