布尔网络动态行为研究*
2012-12-17王向红刘莉莉刘文斌
王向红, 王 欣, 刘莉莉, 许 鹏, 刘文斌
(1.温州大学物理与电子信息学院,浙江 温州 325035;2.温州职业技术学院,浙江温州 325035)
0 引言
1969年,Kauffman[1]提出了著名的布尔网络(Boolean Network,BN)模型,用于研究基因调控网络和细胞分化过程.他将基因的表达分为2种形式:表达(1)和不表达(0),通过布尔函数描述基因之间的相互作用.这种网络模型简单,对数据的数量和质量要求较低,能够反映系统运行过程中的动态特性,为网络控制中出现的非线性动力学行为提供了很好的近似.因此,布尔网络成为研究基因调控网络的重要模型.目前,布尔网络已经广泛应用于酵母细胞周期表达、哺乳动物细胞周期表达、果蝇体节极性网络、花发育形态表达等不同生物的基因调控网络的研究[2-6].本文首先介绍布尔网络及动态行为的相关概念,采用计算机模拟节点数n=20的布尔网络,用消除趋势波动分析(DFA)方法研究其长程相关性动态行为的演化.
1 布尔网络的概念
布尔网络是由一个包含n个基因的节点集{σ1,σ2,…,σn}和一个布尔函数列表{f1,f2,…,fn}组成.每个基因的状态σi∈{0,1}(i=1,2,…,n)是一个二值变量,它在t+1时刻的状态完全由t时刻基因 σj1,σj2,…,σjki的值根据布尔函数 fi:{0,1}ki→{0,1}确定.因此,t+1 时刻状态可以写为

式(1)中:ki表示第i个基因的连通度;σi代表节点i的状态;σi=1表示节点i表达;σi=0表示节点i不表达.基因的状态是由基因的连通度和布尔函数共同决定的.由网络的n个节点的状态{σ1,σ2,…,σn}所构成的向量称为布尔网络的状态,由n个基因组成的网络,其可能的状态数为2n.布尔网络的状态分为暂态和吸引子.由于布尔网络内在规则的方向确定性以及布尔网络状态的有限性,系统进入某些状态后将会无限期地停留在这些状态上,如果没有扰动,系统就很难跳出这些0状态,我们将这些状态称为吸引子.系统具体进入哪个吸引子是由系统演化的初始状态决定的[7].吸引子外围,最终能够演化到特定吸引子的状态,被称为吸引子的吸引域.一般来说,一个系统可以有多个吸引子,如图1所示,一个节点数n=5的随机布尔网络共有25=32个状态,5个吸引子环,系统从任何一个状态开始演化,最终都将进入到吸引子00000,00100,10011,11111和吸引子环11110和11010.

图1 包含5个节点的随机布尔网络的状态空间[8]
1995年,Kauffman[8]使用布尔网络研究控制网络时提出单个吸引子通常对应细胞的某种显型或细胞分化过程的不同阶段.1999年,哈佛大学的Huang Sui[9]提出了布尔网络的吸引子代表系统的一种记忆形式.随后Huang Sui又提出了对吸引子的另外一种理解——吸引子代表细胞的状态,如增生、凋亡、分化等.2006年,Huang Sui等[10]通过对同一白血病细胞株HL-60分别加入DMSO和atRA,7 d后2个细胞群体达到相同的状态,从而在实验上证明了细胞群状态演化中吸引子的存在.
系统的状态一般分布在不同的吸引子区域.随着时间的演化,系统会根据初始状态和布尔规则,逐渐从暂态向吸引子演化.在有扰动的情况下,系统的状态还会在不同吸引子区域之间动态跃迁,显示出复杂的动态.对其进行分析和研究可以再现基因调控网络系统复杂的动力学过程.
2 布尔网络动态行为特性
研究系统的动态主要是研究系统状态在一个非常小的扰动下的演化行为,即扰动后系统是否会回到原来的吸引子或者一个稳定的状态分布.2004年,Shmulevich等[11]提出了布尔网络灵敏度(Sensitivity)的概念,这一概念的提出为以后的布尔网络动态特性的研究提供了极大的方便.
当2个状态向量其汉明距离为1,即2个向量仅有1位不同时,为汉明邻接向量.布尔网络灵敏度Sf(y)定义为:向量y的所有汉明邻接向量的布尔函数f输出值与向量y的布尔函数f(y)输出值不同的邻接向量个数.表述为
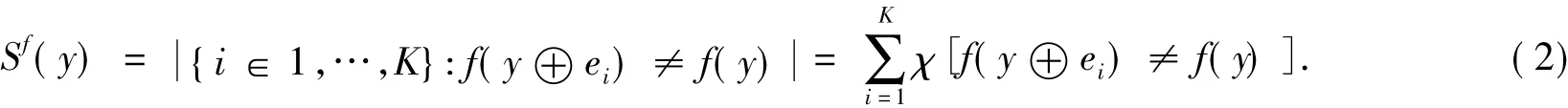
式(2)中:ei为单位向量,其第i位为1,其他位为0;χ[A]为指示函数,当且仅当A为真时χ[A]值为1.在向量y的某种分布下,平均灵敏度(average sensitivity)Sf表示为

平均灵敏度Sf的值介于0和K之间,通常0<Sf<1,Sf=1和Sf>1分别对应系统的有序(Order)、临界(Criticality)和无序(Chaos)[7]状态[12].布尔网络灵敏度是一种衡量网络动态行为的参数,表征网络对一个单位的汉明扰动的平均传播特征,即该扰动是逐渐消失?还是保持不变?还是逐渐扩大[13]?
目前对随机布尔网络的动态行为的研究方法主要分为2类:1)Derrida曲线法;2)长程相关性.下面将详细介绍随机布尔网络的这2种网络动态行为的研究方法.
2.1 Derrida 曲线法
设 ya(t)=(σa1,σa2,…,σan)和 yb(t)=(σb1,σb2,…,σbn)是时刻 t网络的2 个随机选择的网络状态,定义归一化的汉明距离[14]为

式(4)中⊕是异或运算.给定一个随机布尔网络,ρ(t+1)是ya(t)和yb(t)后继状态的汉明距离,ρ(t+1)随ρ(t)变化的曲线称为Derrida曲线.
运行在有序状态的网络,其相近的状态趋向于收敛到同一状态,Derrida曲线位于主对角线以下(见图2).初始很小的汉明距离ρ(t)到ρ(t+1)数值的增大意味着Derrida曲线位于主对角线之上,其斜率在原点附近大于1.这意味着一个很小的基因扰动最终导致完全不同的状态,即网络对初始状态非常敏感——这正是无序状态的特征之一.临界状态的网络,其斜率在原点附近等于1.对于较小的ρ(t),Derrida曲线位于主对角线之上的面积越大,网络就越无序.
对于一个基因数目为n、连通性为K、偏斜度为p的随机布尔网络,当K2p(1-p)>1时,系统为无序;当K2p(1-p)<时,系统为有序;当K2p(1-p)=1时,系统为临界,所以临界连通度Kc为

图2 一个与有序、临界和无序动态特性对应的Derrida曲线的示意图

图3为式(5)所确定的临界曲线,无序状态占据了大部分的参数空间.对大部分的偏斜度p,临界连通度Kc都非常小.对于连通度Kc较大的网络,如果希望其处于有序状态,就必须调整偏斜度p使其远离无偏状态.
2.2 长程相关性
1925年,Johnson在“低频电路中的肖特基效应”中首次提出了“1/f波动”这一术语.20世纪70年代,日本著名物理学家武者利光从混沌学的领域经过多次测量,得出了如下结论:1/f波动之所以令人感觉舒适,主要因为人在安静状态下的心跳周期的波动规律及α脑波的波动规律与1/f波动规律相吻合[15-17].虽然这种波动对基础研究和临床试验都很重要,但是产生这种波动的原因仍然未知[14,18].

图3 随机布尔网络中,由连通度K和偏斜度p确定的临界曲线
2004 年,Amaral等[19]在 Kauffman 的随机布尔网络模型和Wolfram的细胞自动机模型的基础上,研究了不同的布尔规则和连通度对一维环状结构网络动态行为的影响并通过添加噪声研究了网络的鲁棒性.Heneghan等[20]使用消除趋势波动分析(DFA)方法量化系统的长程相关性.图4为其模拟计算结果,得出了系统在不同的布尔规则下长程相关性不同,只有在某些特定的规则下(如232规则)才会出现1/f波动.他们对随机布尔网络的动态行为进行了简单分析,得出布尔网络并不能产生1/f低频功率谱衰变这一结论.布尔网络的动态演化是否能产生1/f低频功率谱衰变对基因调控具有重要的意义.因此,运用计算机动态模拟布尔网络的演化过程,并用DFA方法进一步研究分析布尔网络的动态特性.
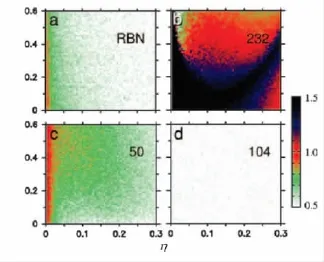
图4 系统在不同布尔规划下演化的长程相关性
3 结果与讨论
在本次布尔网络计算机模拟中,笔者选取的节点数n=20,时间尺度范围是10≤t≤103.图5中纵坐标表示灵敏度,其范围是0.7≤S≤1.3,最小分度为0.02,共有31个数据点;横坐标表示添加噪声范围0.000 5≤p≤0.02,最小分度为0.000 5,共有40个数据点.即图5的面积子图由40×31=1 240个数据点构成.对每一个灵敏度,笔者建立20个网络,每个网络在同一噪声下演化20次.同一灵敏度、同一噪声下表征网络长程相关性值α是20×20=400个数值的平均.2个子图分别表示连通度k=3和k=4的布尔网络长程相关性的变化情况.
从图5可以看出,布尔网络模型的长程相关性的动态变化是比较有规律的.首先,随着噪声的增加,绝大多数网络的长程相关性值逐渐减小;其次,绝大多数布尔网络演化过程能够出现我们所期望的1/f波动范围0.9≤α≤1.1,虽然与Amaral等模拟的网络一样均出现了1/f波动,但是噪声范围不同;最后,从图5还可以看出,不同连通度呈现出来的1/f波动区域宽度不同,k=3时的宽度要比k=4时的宽,说明连通度低的网络更具有稳定性,这与图3中反映的网络状态与平均连通度和偏斜度的关系是一致的.

图5 布尔网络长度相关性值α与噪声及灵敏度的关系
图6 表示灵敏度对布尔网络动态行为的影响,可以看到,随着布尔函数灵敏度数值的增加,网络的长程相关性数值整体往下偏移,网络呈现的1/f波动区域向右移动,即由无序状态渐渐进入有序状态.这是由于灵敏度是一种衡量网络动态行为的参数,表征布尔网络对微小扰动的敏感程度,而长程相关性值表征的是系统对其动态演化状态的记忆行为.所以,灵敏度数值较低的网络,其稳定性相对较高,外界的扰动较难影响网络的演化,网络较易记忆原有的演化轨迹,故长程相关性较强.灵敏度数值较高的网络,网络稳定性相对较弱,外界微小的扰动就能引起系统状态较大的波动,网络较易脱离原有的演化轨迹,所以长程相关性较弱.也就是说有序网络产生的1/f波动范围比无序网络要宽,抗干扰能力强.

图6 布尔网络的长程相关性与灵敏度的关系
4 结束语
作为一种数学模型,布尔网络已经广泛应用于基因调控网络的建模、动态行为分析及网络干预的研究.本文研究了在噪声扰动下,布尔网络的长程相关性.结果表明:随着噪声的增大,大多数的网络都能经过从布朗噪声到1/f,最后到白噪声的相变过程.由于已有很多研究生命系统具有1/f特征,这一研究表明在微观层次上基因调控网络的运行也具有1/f特征.当然,不同网络的1/f的噪声范围各不相同,笔者下一步将主要研究影响1/f噪声范围的原因及1/f这一特征与网络干预方面的关系.
[1]Kauffman S A.Metabolic stability and epigenesis in randomly constructed genetic nets[J].J Theoret Biol,1969,22(3):437-467.
[2]Li Fangting,Long Tao,Lu Ying,et al.The yeast cell-cycle network is robustly designed[J].Proceedings of the National Academy of Sciences of the United States of America,2004,101(14):4781-4786.
[3]Faure A,Naldi A,Chaouiya C,et al.Dynamical analysis of a generic Boolean model for the control of the mammalian cell cycle[J].Bioinformatics,2006,22:124-131.
[4]Albert R,Othmer H G.The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster[J].Journal of Theoretical Biology,2003,223(1):1-18.
[5]Espinosa-Soto C,Padilla-Longoria P,Alvarez-Buylla E R.A gene regulatory network model for cell-fate determination during Arabidopsis thaliana flower development that is robust and recovers experimental gene expression profiles[J].The Plant Cell,2004,16(11):2923-2939.
[6]Chen Lan,Cai Lun,Geir S,et al.Analysis of transcriptional regulation collaboration networks in saccharomyces cerevisiae[J].Progress in Biochemistry and Biophysics,2008,35(1):35-42.
[7]Shmulevich I,Dougherty E R.基因组信号处理[M].刘文斌,高琳,译.北京:科学出版社,2010.
[8]Kauffman S A.Search strategies for applied molecular evolution[J].Journal of Theoretical Biology,1995,173(4):427-440.
[9]Huang Sui.Gene expression profiling,genetic networks,and cellular states:an integrating concept for tumorigenesis and drug discovery[J].Journal of Molecular Medicine,1999,77(6):469-480.
[10]Huang Sui,Ingber D E.A non-genetic basis for cancer progression and metastasis:self-organizing attractors in cell regulatory networks[J].Breast Disease,2006,26:27-54.
[11]Shmulevich I,Kauffman S A.Activities and sensitivities in Boolean network models[J].Physical Review Letters,2004,93(4):048701.
[12]Goldberger A L,Amaral L A N,Haussdorf J M,et al.Fractal dynamics in physiology:Alterations with disease and aging[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(1):2466-2472.
[13]Shmulevich I,Kauffman S A.Activities and sensitivities in Boolean network models[J].Physical Review Letters,2004,93(4):08701.
[14]Derrida B,Pomeau Y.Random networks of automata:a simple annealed approximation[J].Europhys Letters,1986,1(2):45-49.
[15]Peng C K,Havlin S,Stanley H E,et al.Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time-series[J].Chaos,1995,5(1):82-87.
[16]Ivanov P C,Nunes-Amaral L A,Goldberger A L,et al.Multifractality in human heartbeat dynamics[J].Nature,1999,399(6735):461-465.
[17]Amaral L A N,Ivanov P C,Aoyagi N,et al.Behavioral-independence features of complex heartbeat dynamics[J].Physical Review Letters,2001,86(26):6026-6029.
[18]Lipsitz L A.Dynamics of stability:The physiologic basis of functional health and frailty[J].J Gerontol A Biol Sci Med Sci,2002,57(3):B115-B125.
[19]Amaral L A N,Moreira A A,Goldberger A L,et al.Emergence of complex dynamics in a simple model of signaling networks[J].Proceedings of the National Academy of Sciences of the United States of America,2004,101(44):15551-15555.
[20]Heneghan C,McDarby G.Establishing the relation between detrended fluctuation analysis and power spectral density analysis for stochastic processes[J].Physical Review Letters,2000,62(5):6103-6110.
