Banach空间中向量均衡问题近似解的最优性条件*
2012-12-17鲍玲玲仇秋生
鲍玲玲, 仇秋生
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引言
向量均衡问题是优化理论的重要组成部分,向量变分不等式、向量优化、向量Nash平衡及向量互补性问题等都是向量均衡问题的特例.近20多年来,许多学者研究了向量均衡问题解的存在性和解的性质[1-9],但关于向量均衡问题解的最优性条件的研究比较少.Giannessi等[3]在有限维空间中把带约束的向量变分不等式问题转化成无约束的向量变分不等式问题,并给出了有效解与弱有效解的充分条件;Morgan等[10]应用次微分的概念,在Hilbert空间中给出了向量广义拟变分不等式问题的弱有效解的标量化及K-T条件;龚循华[11]在局部凸空间中给出了带约束的锥凸向量均衡问题解的最优性条件;仇秋生[12]获得了广义凸向量均衡问题弱有效解的充分与必要条件;戎卫东等[13]引进了向量均衡问题的ε-弱有效解的概念,给出了集值向量均衡问题的ε-弱有效解的存在性结果;杨晓奇等[14]引进了向量变分不等式问题的ε-近似解的概念,得到了Banach空间中向量变分不等式问题的ε-有效解的最优性条件;Gutierrez等[15]研究了向量优化问题的Tanaka近似解的性质,通过标量化给出了近似解的充分与必要条件;龚循华等[16]获得了Banach空间中无约束向量均衡问题的ε-解的最优性条件.本文在文献[11-16]的基础上,首先讨论了向量均衡问题近似解的一些性质;其次,引进了带约束向量均衡问题的ε-有效解、ε-弱有效解的概念,研究了带约束向量均衡问题的ε-有效解、ε-弱有效解的充分与必要条件,改进和推广了文献[14,16]的主要结果.
1 定义与引理
若无特别申明,以下总假设X,Y,Z为Banach空间,X*为X的共轭空间,D为X的非空子集,0为Y的零元,U为 Y中的闭单位球,C⊂Y和 K⊂Z为2个点凸锥.设 g:D→Z,F:D×D→Y,且∀x∈D,

设S为X的任意一个非空子集,用cl S,int S分别表示S的闭包和内部.C的共轭锥用C*表示,即
其中,P∪{0}为Y中的凸锥.

2)映射 f:D→Y 在 D 上称为 C-次类凸的,若存在 θ∈int C,使得∀x1,x2∈D,∀λ∈[0,1],∀ε >0,存在 x3∈D,有 εθ+f(x1)+(1-λ)f(x2)-f(x3)∈C.
注1[17]1)f是C-类凸的当且仅当 f(D)+C是凸集;f是C-次类凸的当且仅当 f(D)+int C是凸集.
2)若f是C-类凸的,则一定是C-次类凸的;反之一般不成立.
引理1[14]令M={y∈Y:y+U⊂-int C},且r0=d(0,M),则 M 是一个内部非空的凸集且r0≥1.
引理2[18]设C⊂Y为内部非空的点凸锥.
1)若 c*∈C*{0},c∈int C,则〈c*,c〉>0;
2)若 c*∈int C*,c∈C{0},则〈c*,c〉>0.
2 向量均衡问题近似解的一些性质
把所有(VEPC)的有效解、弱有效解、ε-有效解、ε-弱有效解组成的集合分别记作 E(F,A,C),WE(F,A,C),AE(F,A,C,ε)和 WAE(F,A,C,ε).
注2 由定义1 和定义2 易得:1)若 int C≠Ø,则 AE(F,A,C,ε)⊂WAE(F,A,C,ε);
2)若0≤ε1≤ε2,则 AE(F,A,C,ε1)⊂AE(F,A,C,ε2);
3)若 ε =0,则 AE(F,A,C,0)=E(F,A,C),WAE(F,A,C,0)=WE(F,A,C).
定理1 设:1)ε≥0,{εn}⊂R+,且 εn→ε;2)对∀y∈A,F(x,y)关于 x 在 A 上连续.则
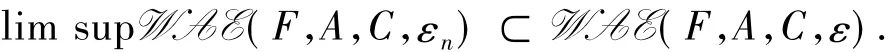
其中,lim supWAE(F,A,C,εn)={x∈A :存在序列{xn},使得 xn∈WAE(F,A,C,εn),xn→x}.
证明 假设结论不成立,则存在 x0∈lim supWAE(F,A,C,εn),但 x0∉WAE(F,A,C,ε).于是,存在 y0∈A,使得

由 x0∈lim supWAE(F,A,C,εn) 知,存在 xn∈WAE(F,A,C,εn)且 xn→x0,从而

又由y0∈A得
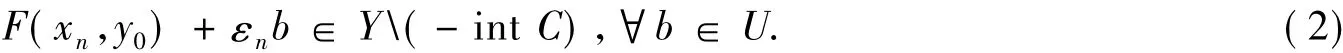
而 F(x,y0)关于 x在 A上连续,Y(-int C)为闭集,且 εn→ε 和 xn→x0,故结合式(2)有 F(x0,y0)+εb∈Y(-int C),∀b∈U,即 F(x0,y0)+εU⊂Y(-int C).这与式(1)矛盾.定理1 证毕.
由定理1可以得到下面的推论:
推论1 设 A 为闭子集,∀y∈A,F(x,y)关于 x在 A 上连续,则 WAE(F,A,C,ε)为闭集.
推论2 设:1)y∈A,F(x,y)关于 x 在 x0处连续;2){εn}⊂R+,{xn}⊂A 且 ε↓0,xn→x0.若对每个n,xn∈WAE(F,A,C,εn),则 x0∈WE(F,A,C).
定理2 设:1)x0∈A,∀y∈A,F(x,y)关于 x 在 x0处连续;2){εn}⊂R+,{xn}⊂A 且 εn↓0,xn→x0;3){F(xn,y)}为单调增序列(即∀m > n,F(xn,y)∈F(xm,y)-C),且 C 为闭集.若对每个 n,xn∈AE(F,A,C,εn),则 x0∈E(F,A,C).
证明 假设 x0∉E(F,A,C),则存在 y∈A,使得 F(x0,y)∈ -C{0},即

由{F(xn,y)}为单调增序列知,对∀m>n有

又对 y∈A,F(x,y)关于 x在 x0处连续和 xm→x0知

由式(5)及 C 为闭集,在式(4)中令 m→∞,有 F(x0,y)∈F(xn,y)+C,∀n∈N,从而

而 xn∈AE(F,A,C,εn),即 F(xn,A)⊂Y((-C){0})+εnU,也就是

于是,(F(xn,A)-εnU)∩(-C)={0}.由式(6)知

从而 F(xn,y)={0},由式(5)有 F(x0,y)=0.这与式(3)矛盾.定理 2 证毕.
3 最优性条件

又A⊂D,由式(8)可知,


证明 若ε=0,则由式(11)有
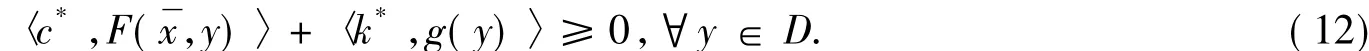
又A⊂D,由式(12)可知
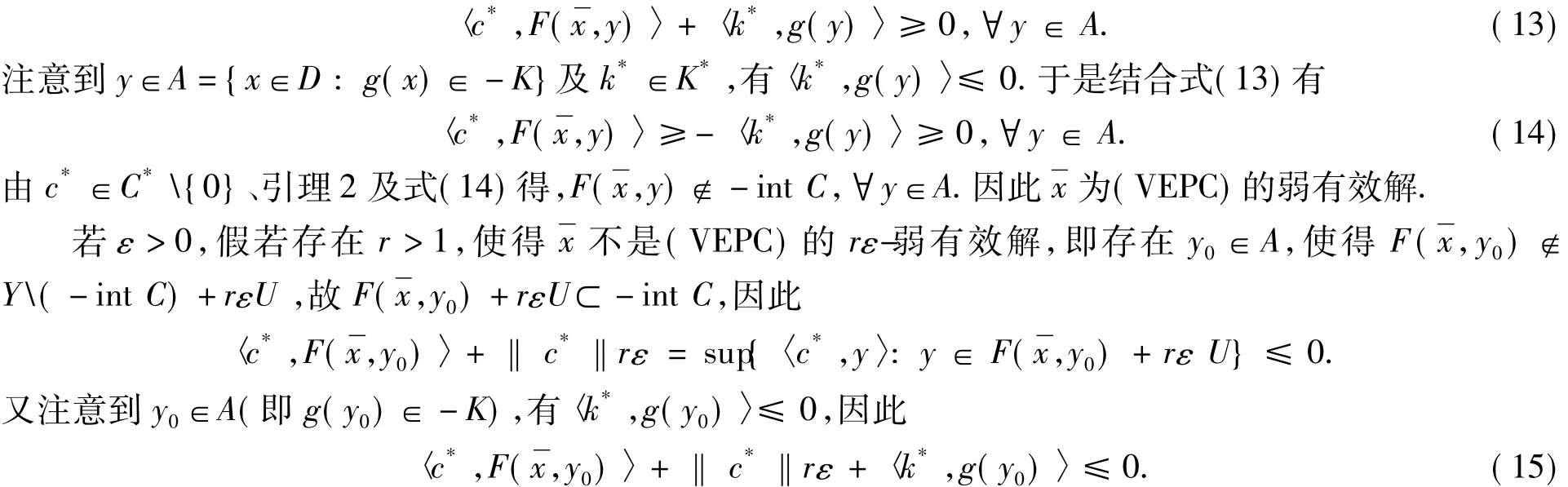
从而,由‖c*‖=1及式(15)可知

式(16)中,r0如引理1的定义.

从而

结合C,K为凸锥,得

由式(19)及式(20)知
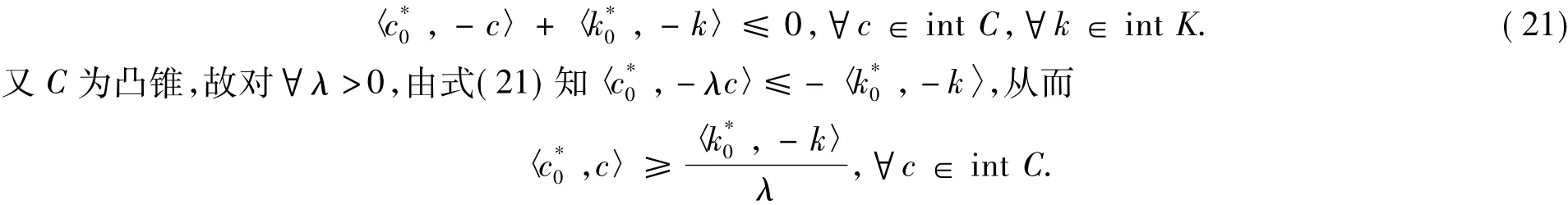
令λ→∞,有

同式(19)的证明可得

结合式(29)及〈k*,-int K〉≤0,可知式(16)成立.定理5证毕.
注3 定理5将文献[16]的定理2.2作了以下推广:
1)将无约束向量均衡问题推广为带约束向量均衡问题;
2)将目标函数由类凸映射推广为次类凸映射.
[1]Ansari Q H,Oettli W,Schläger D.A generalization of vectorial equilibria[J].Mathematical Methods of Operation Research,1997,46(2):147-152.
[2]Bianchi M,Hadjisavvas N,Schaible S.Vector equilibrium problems with generalized monotone bifunctions[J].J Optim Theory Appl,1997,92(3):527-542.
[3]Giannessi F,Mastroeni G,Pellegrini L.On the theory of vector optimization and variational inequalities.Image space analysis and separation[C]//Giannessi F.Vector variational inequalities and vector equilibria:mathematical theories.Dordrecht:Kluwer Academic Publishers,2000:153-215.
[4]Ansari Q H,Konnov I V,Yao J C.Characterizations of solutions for vector equilibrium problems[J].J Optim Theory Appl,2002,113(3):435-477.
[5]Fu J.Simultaneous vector variational inequalities and vector implicit complementarity problems[J].J Optim Theory Appl,1997,93(1):141-151.
[6]Gong X H.Connectedness of the solution sets and scalarization for vector equilibrium problems[J].J Optim Theory Appl,2007,133(2):151-161.
[7]Gong X H.Efficiency and henig efficiency for vector equilibrium problems[J].J Optim Theory Appl,2001,108(1):139-154.
[8]Hadjisavvas N,Schaible S.From scalar to vector equilibrium problems in the quasimonotone case[J].J Optim Theory Appl,1998,96(2):297-309.
[9]Kimura K,Yao J C.Sensitivity analysis of vector equilibrium problems[J].Taiwanese Journal of Mathematics,2008,12(3):649-669.
[10]Morgan J,Romaniello M.Scalarization and Kuhn-Tucker-like conditions for weak vector generalized quasivariational inequalities[J].J Optim Theory Appl,2006,130(2):309-316.
[11]Gong Xunhua.Optimality conditions for vector equilibrium problems[J].Journal of Mathematical Analysis and Applications,2008,342(2):1455-1466.
[12]Qiu Qiusheng.Optimality conditions for vector equilibrium problems with constraints[J].Journal of Industrial and Management Optimization,2009,5(4):783-790.
[13]Rong W D,Jia Y Z,Du Z J.Topological properties of ε-solutions sets for vectorial equilibria[J].OR Transactions,2001,5(2):1-11.
[14]Yang X Q,Zheng X Y.Approximate solutions and optimality conditions of vector variational inequalities in Banach spaces[J].J Glob Optim,2008,40(1/2/3):455-462.
[15]Gutierrez C,Jimenez B,Novo V.Optimality conditions for metrically consistent approximate solutions in vector optimization[J].J Optim Throry Appl,2007,133(1):49-64.
[16]龚循华,熊淑群.Banach空间中向量均衡问题的近似解的最优性条件[J].南昌大学学报:理科版,2010,34(2):103-107.
[17]Jeyakumar V.A generalization of a minimax theorem of fan via a theorem of the alternative[J].J Optim Theory Appl,1986,48(3):525-533.
[18]Jahn J.Mathematical vector optimization in partially ordered linear spaces[M].Frankfurt:Verlag Peter Lang,1986.
