一类Roper-Suffridge算子的性质

崔艳艳,王朝君

(周口师范学院数学系,河南周口466001)

则称f(z)是Ω上α次β型螺形映照;若取β=0,即为Ω上α次星形映照的定义。

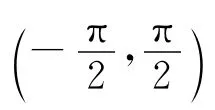
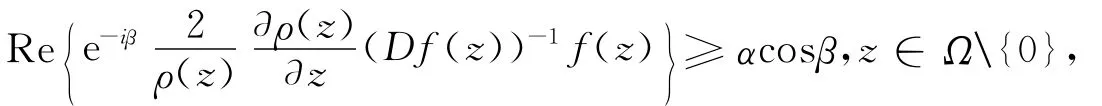
则称f(z)是Ω上α次殆β型螺形映照。若取β=0,即为Ω上α次殆星形映照的定义;取α=0,即为Ω上β型螺形映照的定义。若取α=β=0,即为Ω上星形映照的定义[2]。

α次强β型螺形映照是由冯淑霞和刘太顺[1]引入的,本文将其推广到有界星形圆型域上。

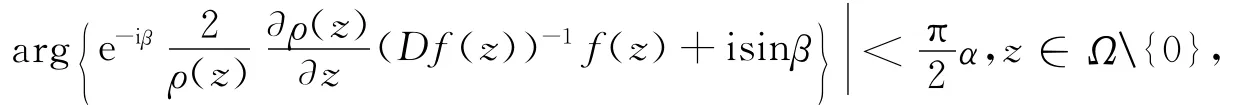
则称f(z)是Ω上α次强β型螺形映照。若取β=0,即为Ω上α次强星形映照的定义。

则称f(z)是Ω上强β型螺形映照。若取β=0,即为Ω上强星形映照的定义。

2008年,陈慧勇给出Cn中单位球Bn上的ρ次抛物星形映照[4]的定义,这里将其推广到有界星形圆形域上。

定义5 设Ω,f同定义1。若ρ∈[0,1),

则称f是Ω上ρ次抛物星形映照。当ρ=0时,即为抛物星形映照。

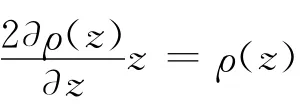
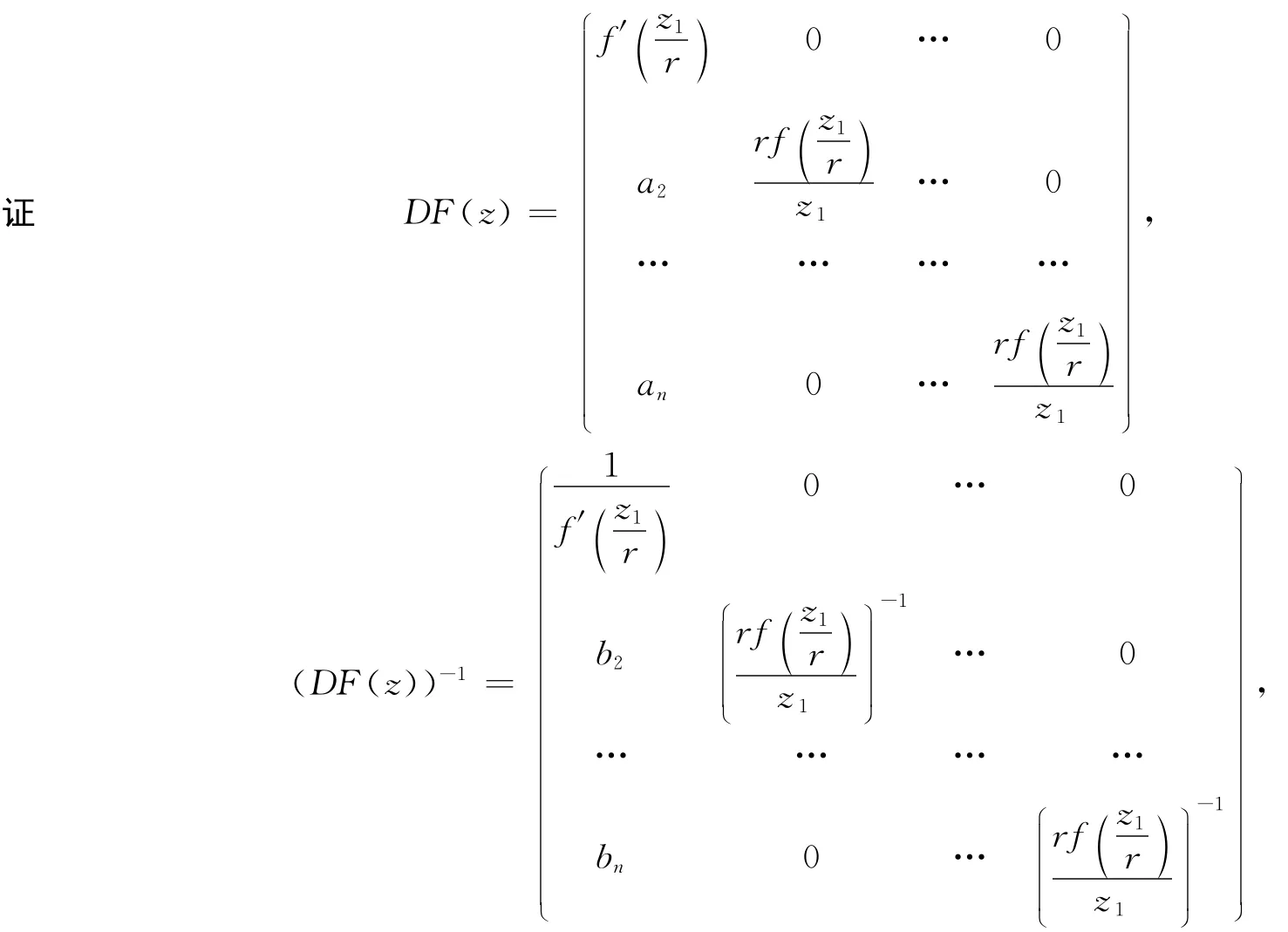
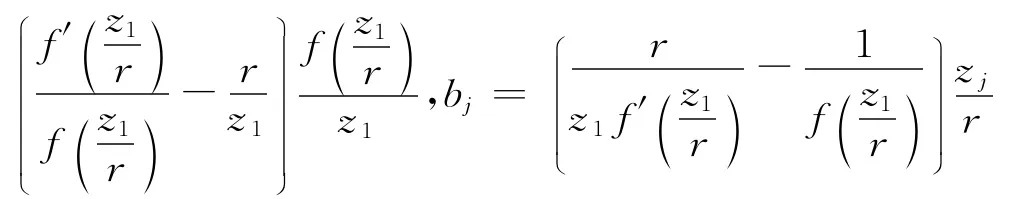
经计算可知,

由定义1知,F(z)是Ω上α次β型螺形映照,即

将式(1)代入上式并由引理1得

在定理1中分别令β=0,则得到相应的α次星形映照的结论。

证 由定义2知,F(z)是Ω上α次殆β型螺形映照,即

将式(1)代入上式并由引理1得

类似定理1的证明可知,F(z)是Ω上α次殆β型螺形映照当且仅当f是D上的α次殆β型螺形映照。

在定理2中分别令α=0,β=0则得到相应的β型螺形映照及α次殆星形映照的结论。

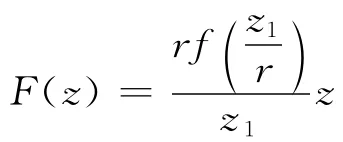
利用定义3,证明类似定理1的证明,这里省略。

令β=0则得到相应的α次强星形映照的结论。

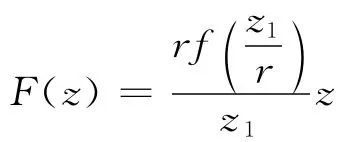
类似定理1并结合定义4及定义5有以下结论:

[1]Feng S X,Liu T S.The generalized Roper-Suffrideg extention operator[J].Acta,Math.Sci.,2008,28B(1):63-80.

[2]Gong S.Convex and Starlike Mappings in Seversl Complex Variables[M].[S.l.]:Kliwer Academic Publishers,1998.

[3]于琳.有关全纯映照的两类Roper-Suffridge算子[D].河南大学硕士论文,2010.

[4]陈慧勇.多复变函数的抛物星形映射[D].河南大学硕士论文,2008.

[5]Liu T S,Ren G B.The growth theorem for starlike mappings on bounded starlike circular domains[J].Chin.Ann.of Math.,1998,19B(4):401-408.