神经网络初始条件对似大地水准面拟合结果的影响

宋 雷，胡伍生，丁 超

(1．东南大学交通学院，江苏 南京210096;2．山东交通学院土木工程学院，山东 济南250357)

一、引 言

在组合法确定高精度、高分辨率似大地水准面的过程中，是将利用重力数据计算的高分辨率重力似大地水准面拟合到高精度但分辨率较低的GPS/水准似大地水准面上，形成即具有高精度又具有高分辨率的可应用模型[1-2]。将重力似大地水准面拟合到GPS/水准似大地水准面的方法主要有多项式拟合法、最小二乘配置法等[3-6]。人工神经网络属于自适应非线性动力学系统，研究已表明两层网络在隐含层和输出层选择合适传输函数的情况下，只要隐含层有足够的神经元，几乎可以以任意精度逼近任何感兴趣的函数。在测绘领域，神经网络方法在似大地水准面拟合等方面已有研究，并取得较好的结果[7-8]。但BP神经网络方法存在结果受初始权值和学习集样本子样次序的影响而不稳定的缺点，神经网络初始条件对似大地水准面拟合结果的影响还需进行研究。

本文利用Matlab的BP神经网络工具箱中的BP神经网络仿真程序构造BP神经网络模型，并依据区域实例对BP神经网络的初始权值的设置和学习集样本次序对拟合结果的影响进行研究，进而得出相关结论。

二、基本原理与方法

1．BP神经网络模型的结构

常用的BP神经网络包括3层结构，分别为输入层、隐含层和输出层。隐含层是可以并行操作的神经元的集合，隐含层中每个神经元包含一个偏置值、一个累加器、一个传输函数和一个输出，输入向量的每个元素通过权值矩阵和神经元相连。本文研究中，隐含层采用对数-S形函数(log-sigmoid函数)，输出层采用线性函数(pureline函数)。因为sigmoid函数标准输入、输出限定为[0，1]，所以在网络中增加了输入(出)转换层，将学习集的GPS点的大地坐标和高程异常差转化到限定区间[9-10]。本文研究限定在[0．2，0．8]中，以避开网络输出的饱和区，5层神经网络结构如图1所示。

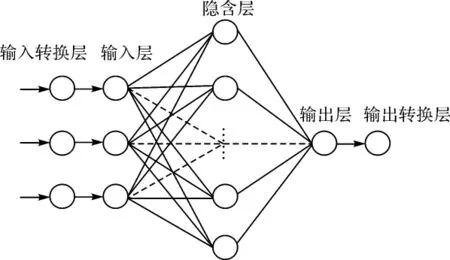
图1 5层神经网络结构

2．区域重力似大地水准面

选用经度115．0°～120．0°，纬度 35．0°～38．0°为研究区域，区域内重力似大地水准面采用移去-恢复法计算，高程异常分为两部分，第一部分是由重力场模型(选用IGG05B模型)计算的模型高程异常;第二部分由地面观测重力异常移去IGG05B模型重力异常和局部地形改正得到的残差Faye异常计算。取Molodensky级数的一阶项近似等于重力局部地形改正，将Molodensky级数的零阶项与一阶项合并，按Stokes公式计算残差高程异常Δζ，并顾及Faye异常代替严格一阶项应加的3个改正项严密表达式，计算公式为

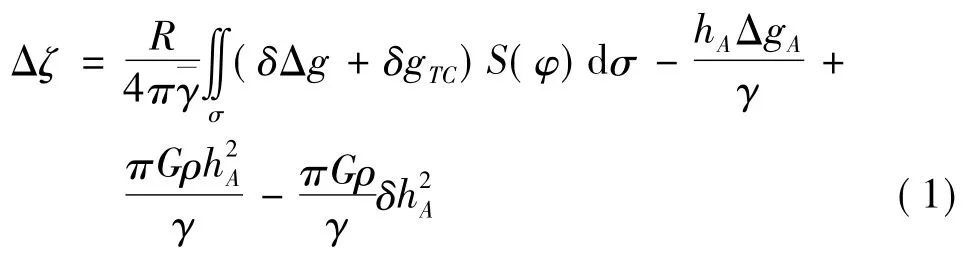
式中，R为地球平均半径;¯γ为正常重力均值;δΔg残差空间异常;δgTC为局部地形改正;φ为计算点和流动点之间的角距;S(φ)为Stokes函数;dσ是单位球面上的面元;hA、ΔgA分别为计算点的高程(由DEM数据得到)和空间异常;ρ为地壳密度，一般取2．67 g/cm3;为全球地形高平方h2的球谐展开零阶和一阶项之和。模型高程异常ξM与残差高程异常Δξ之和即为恢复后的高程异常，这样就得到重力似大地水准面格网数值模型。

3．区域似大地水准面整体拟合的BP神经网络算法

利用重力似大地水准面模型内插GPS/水准点模型高程异常ξ1，从GPS/水准点实测高程异常ξ2中减去ξ1组成高程异常差序列Δξ。由于高程异常差与点位的平面位置密切相关，而与点位的高程相关性不大，将输入层元素取为点位的大地坐标(B，L)，输出层元素取为高程异常差Δξ，利用所有控制点的信息组成学习集样本

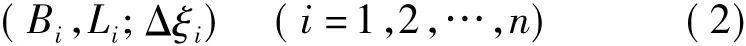
构造BP神经网络模型，利用给定学习集样本对网络进行训练，搜索参数区间，获得网络响应和GPS/水准点表现的高程异常差之间差值的均方误差最小。

用训练好的神经网络参数求似大地水准面规则格网上的高程异常差Δξ，重力似大地水准面格网上的高程异常加高程异常改正数Δξ完成将重力似大地水准面拟合到GPS/水准似大地水准面上。

三、实例计算

1．GPS/水准数据

选用经度 115．2°～116．6°，纬度 35．8°～37．0°为研究区域，收集到区域内可应用C级GPS网点81个，点间平均距离为10 km。该区域地形比较平坦，没有大的起伏，面积约为8000 km2。GPS网采用双频GPS接收机施测，对接收机的高程相位进行了改正，作业方式为经典静态相对定位测量模式，控制网在WGS-84下无约束平差，点位中误差的数量级均为毫米级。每个C级GPS网点均以三等精度进行了水准观测，高程系统采用1985国家高程基准。平差后最大高程中误差为±2．31 cm。GPS/水准点与重力似大地水准面高程异常差起伏大于0．5m。该区C级GPS/水准点分布如图2所示。

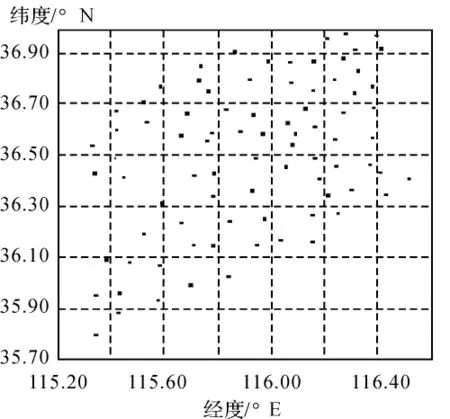
图2 区域GPS/水准点分布

2．BP神经网络隐含层隐含层神经元个数设计

输入层和输出层结构是由实际问题本身决定的，隐含层数量和各隐含层神经元数目应根据学习集样本数量和研究问题的复杂程度进行调整。隐含层神经元数目少，网络难以逼近有大量拐点的函数，隐含层神经元数目多，会导致在应用中出现对训练样本集达到较高的匹配效果，但对新的输入样本矢量却可能会产生与目标矢量差别较大的输出，即网络具有较差的推广能力。精确预测隐含层所需要的神经元的数目至今仍然存在一些理论上还没有解决的问题，在神经网络中，Ockham的“剃刀”理论提出：只要有一个更小的网络能工作，就不要使用更大的网络。。本文试验中BP神经网络使用的，隐含层神经元单元个数设计为5个，选用2-5-1网络进行研究。

3．学习集样本子样次序对结果的影响

人工神经网络对样本的次序具有敏感性，利用本文研究设计的神经网络，进行了如下计算比较试验：①子样按纬度由小到大排列与按纬度由大到小排列计算结果差;②子样按经度由小到大排列与按经度由大到小排列计算结果差;③子样两次随机排列的结果差。在隐含层选用5个神经单元，每次计算的初始权值都随机设置，学习集样本次序对两区域拟合结果差等值线如图3～图5所示。

从图3～图5的比较，学习集子样按3种不同次序排列所得计算结果之差除在测区边缘控制点缺少部分两次结果差值大于10．0毫米外，控制点控制区域内不同子样排列顺序的结果差异均小于2．0mm或者更小。这说明子样排列顺序在GPS/水准点控制区域内对结果的影响是较小的，在确定厘米级区域似大地水准面的过程中，GPS/水准点控制区域内学习集样本子样次序对结果的影响可忽略。

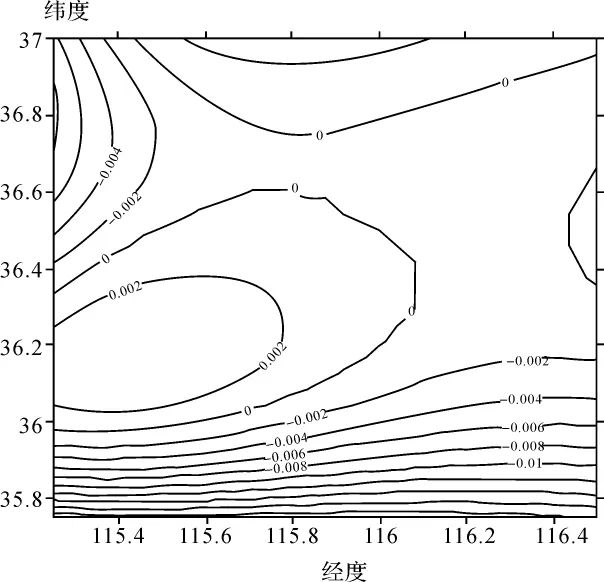
图3 学习集样本按纬度不同顺序排列计算结果差

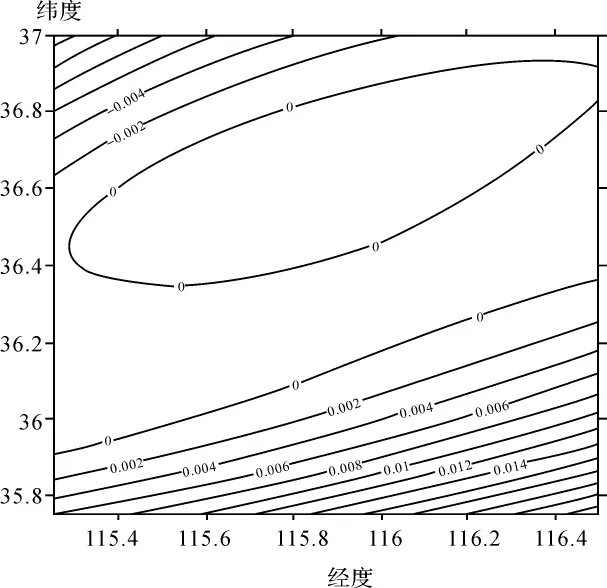
图4 学习集样本按经度不同顺序排列计算结果差

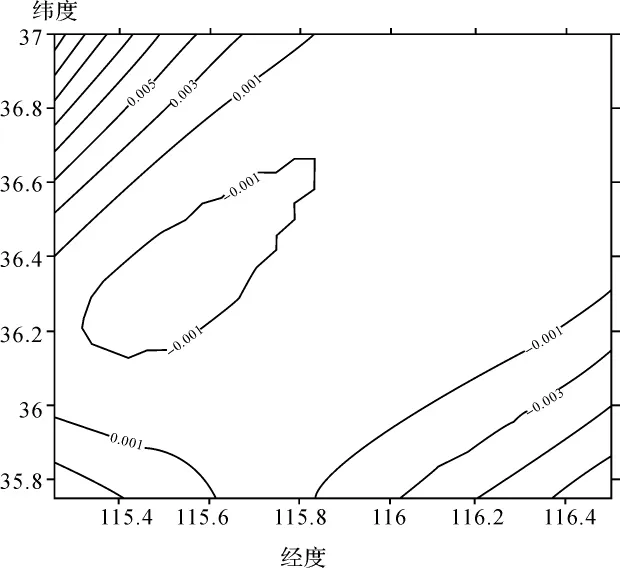
图5 学习集样本两次随机排列的计算列计算结果差

4．初始权值的设置对结果的影响

BP神经网络Matlab仿真程序中，权值的初始化是通过rands命令产生-1．0到1．0之间随机取值再除以10来实现，初始权值随机赋值为接近于零的非零值，可以在不离开性能曲面平坦区域的同时避开可能的鞍点。由于初始权值是随机产生的，不同的初始权值会对最终结果产生影响(这也是人工神经网络在工程应用中的缺点之一)，在隐含层5个神经单元个数的情况下进行了5次计算，每次计算的初始权值都是随机产生的，5次计算的结果每两次之差可作为考察初始权值的设置对结果的影响(学习集样本子样次序相同)，结果如表1所示。

根据表中比较数据，除最后两次在测区边缘部分两次结果差值略大于10．0毫米外，不同初始权值的结果差异一般在毫米级或者更少。如果收敛到性能曲面的同一极小点，拟合结果几乎没有差异，在实际计算中初始权值的设置对厘米级似大地水准面拟合结果的影响也可忽略。

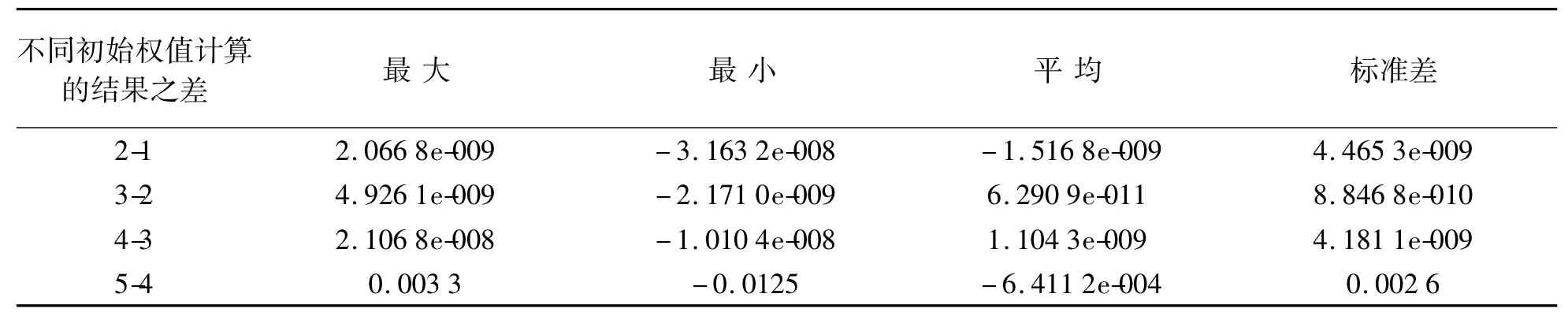
表1 神经网络初始权值的设置对拟合结果的影响m

四、结束语

本文主要针对BP神经网络的初始权值的设置和学习集样本次序对重力似大地水准面和GPS/水准似大地水准面的拟合的结果进行比较，得出在GPS/水准点控制区域内，初始权值的设置和学习集样本次序对结果的影响一般小于2．0mm，远小于测量误差和计算模型误差，对于构建厘米级似大地水准面可忽略其影响的结论。

[1]宁津生，罗志才，李建成．我国省市级大地水准面的现状及技术模式[J]．大地测量与地球动力学，2004，24(1)：4-8．

[2]李建成，陈俊勇，宁津生，等．地球重力场逼近理论与中国2000似大地水准面的确定[M]．武汉：武汉大学出版社，2003．

[3]张全德，郭春喜，王斌．浙闽赣区域似大地水准面精化[J]．测绘科学，2007 ，32(1)：11-17．

[4]DARBEHESHTI N，FEATHERSTONE W E．Tuning a Gravimetric Quasi-geoid to GPSLevelling by Non-stationary Least-squares Collocation[J]．Journal of Geodesy，2010，84(7)：419-431．

[5]张全德，郭春喜，王斌，等．华东、华中区域似大地水准面精化[J]．地理信息世界，2007，05(5)：21-26．

[6]KLEESR ，PRUTKIN I．The Combination of GNSS-levelling Data and Gravimetric(Quasi-)Geoid Heights in the Presence of Noise[J]．Journal of Geodesy，2010，84(12)：731-749．

[7]宋雷，黄腾，方剑．基于贝叶斯正则化BP神经网络的GPS高程转换[J]．西南交通大学学报：自然科学版，2008(6)：679-683．

[8]宋雷，方剑，黄腾．Bayesian正则化BP神经网络拟合两类似大地水准面[J]．武汉大学学报：信息科学版，2009，34(5)：552-555．

[9]胡伍生，华锡生．平坦地区转换GPS高程的混合转换方法[J]．测绘学报，2002，31(2)：128-133．

[10]胡伍生，沙月进．神经网络BP算法的误差分级迭代法[J]．东南大学学报，2003，33(3)：376-378．