基于LS+AR模型的极移预报及其周期项影响分析

孙张振，徐天河，范朋飞

(1．长安大学地质工程与测绘工程学院，陕西西安710054;2．地理信息工程国家重点实验室，陕西西安710054;3．西安测绘研究所，陕西西安710054)

一、引 言

地球的自转运动表征着地球整体的运动状况，由地球各圈层地核、地幔地壳和大气之间的相互作用引起的，可用地球定向参数(earth orientation para meters，EOP)描述[1]。EOP 包括 3 部分：① 章动和岁差;② 极移;③ 日长变化。其中，极移是表征地球运动的重要参数，它用来描述地球瞬时自转轴在地球本体的运动而导致地球极点在地球表面上的位置发生缓慢变化的现象。高精度的极移观测和预测数据对于天球参考框架和地球参考框架具有重要意义，是提高空间导航定位技术精度的必要部分。针对极移的预报，国内外许多学者建立了各种预报模型对其进行研究、预报和监测[2-8]。总的来说，这些模型大部分是将极移分为有规律的确定性部分和无规律的随机性部分，即首先利用最小二乘方法(least squares，LS)来拟合极移时间序列中的趋势项，这些有规律的确定性部分包括极移的长期趋势(LT)、钱德勒摆动(CW)、周年摆动(AW)和半周年摆动(SAW)，并对其进行外推预测;然后利用AR 模型[6]、

ARMA模型或者人工神经网络[9]等确定性或者随机性模型对其残差部分进行预测，最后得到预报的极移结果。在上述预测方法中，利用最小二乘方法拟合其趋势项时，国内外学者在周期项的具体数值上虽大体一致但普遍不同，国外学者在钱德勒周期中选择在433～435 d之间较多。国内学者如许雪晴在极移预报时选取钱德勒周期约为435 d[10]，张昊等钱德勒周期选取为 1．183 a(432．08 d)[11]，在周年项和半周年项上国内外选取比较一致，都为1 a(365．24 d)和0．5 a(182．62 d)。由于在极移观测数据中其周期项和趋势项都有时变性的特点[12]，为了更加精确地进行极移预报，本次在LS+AR预报模型的基础上，在利用最小二乘拟合数据趋势项之前，首先对62 a来的极移数据做频谱分析[13]，由计算结果显示其周期项中钱德勒周期为435．17 d，周年项为365．54 d，半周年项峰值对于X、Y分量有两个峰值，却有微小不同，鉴于其波峰值较小，故仍统一采用182．62 d。因此，此次在进行LS拟合时，应用频谱分析得出的周期项参数，联合AR模型预报极移并与其他学者所用周期项预报结果相比较。计算结果表明，应用本文所选取的周期项进行预报时，其预报精度最高。

二、LS+AR模型

LS+AR模型为一种组合的模型，在对极移进行预报时，首先应用最小二乘拟合趋势项，扣除后得到残差部分，再利用AR模型对残差部分进行预测，结合最小二乘外推部分即可得到预测值。

1．LS模型

在本文中，利用最小二乘外推模型中包含有线性项、半周年项、周年项和钱德勒项，模型公式为

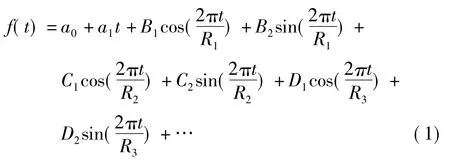
式中，a0为常数项;a1为趋势项;B1、B2、C1、C2、D1、D2…为各周期项拟合系数;R1、R2、R3…分别为周期项中的周期;t为UTC时间。

2．AR模型

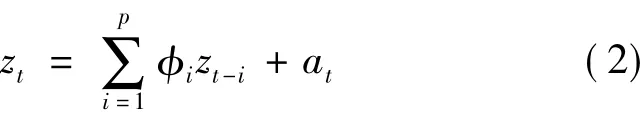
式(2)中，φ1，φ2，…，φp为模型参数;at为白噪声序列;p为模型阶数;式(2)称为p阶自回归模型，简记为AR(p)。

AR模型要求建模的时间序列是平稳随机序列，即满足平稳、正态、零均值的条件。运用AR模型的关键是确定AR模型的阶数p，一般采用最终误差准则、信息论准则、和传递函数准则，实际中这3种方法是等效的。本文采取最终误差准则来确定AR模型的阶数p：

最终误差准则

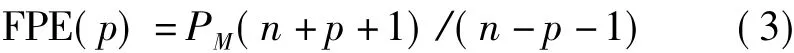
其中

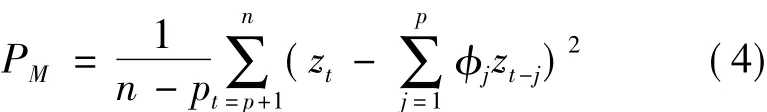
式(4)中使FPE(p)达到极小值的p就取作AR模型的阶数。φ1，φ2，…，φp等模型参数可以通过求解Yule-Walker方程来确定。

3．精度评定

为了便于评估预测精度，采用平均绝对误差(mean absolute error，MAE)作为精度评定标准，其计算公式为

式中，Pi为第i期的预报值;Oi为相应的观测值;Ei为跨度第i期预报的真误差(假定观测值为真值);n为总预报期数;MAEj为预报跨度为j的平均绝对误差。

三、数据计算和结果分析

1．数据说明

本次计算所用到的数据来自国际地球自转和参考系服务IERS发布的EOP 05C04序列(http：∥hpiers．obspm．fr/eoppc/eop/)，该序列包含1962 年1 月1日至今的极移分量Xp和Yp、日长变化LOD、地球自转速率UT1-UTC等，时间间隔为1 d。首先对极移分量Xp和Yp做频谱分析，图1为极移频谱周期分布图，从图上可明显看出极移中钱德勒周期约在435 d和周年周期项约为365 d。结合实际计算数据，可知其中钱德勒周期为435．17 d，周年项为365．54 d。

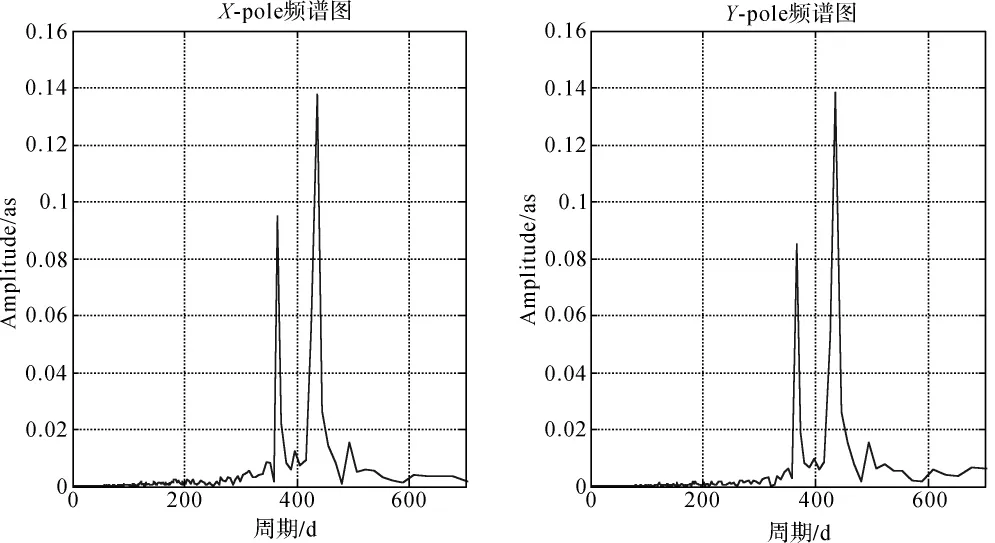
图1 极移频谱分析图

2．数据处理

为了确定极移中具体周期对极移预报精度的影响，本文此次在进行最小二乘拟合时根据以往所采用的周期经验值和本文中所确定的周期值分别对极移进行预报，设计方案如下。

方案一：周期项选取钱德勒周期项432．08 d，周年项365．24 d，半周年项182．62 d。

方案二：周期项选取钱德勒周期项433 d，周年项365．24 d，半周年项182．62 d。

方案三：周期项选取钱德勒周期项435 d，周年项365．24 d，半周年项182．62 d。

方案四：周期项选取钱德勒周期项435．17 d，周年项365．24 d，半周年项182．62 d。

方案五：周期项选取钱德勒周期项435．17 d，周年项365．54 d，半周年项182．62 d。

在对极移(PM)进行预报时，其观测基础序列长度对预报精度有很大的影响，为了提高预报精度，本次预报所应用的都是最优基础序列长度，极移分量X和Y基础序列长度都为10 a观测序列。预报精度结果统计是从2004年1月1日至2012年4月8日，分别对其进行跨度为1～360 d的预报。图2～4给出了以上5种方案的预报精度对比图。

从图2可以看出，钱德勒周期的具体数据选取对极移的预报精度有很大关系，虽然其变化只在3 d内，但越是接近钱德勒周期真值，其极移预报就会越精确。从图3中可知，方案三和方案四预报精度非常接近，方案四更精确一些，也说明本文所用的钱德勒周期数据更加接近于真值。而从图4可以看出，方案五的预报精度要高于方案四，这也可以说明在极移数据中，周年项的具体真值并不是只局限于365．24 d，本文中所应用的周年项数值365．54 d更接近与真值。

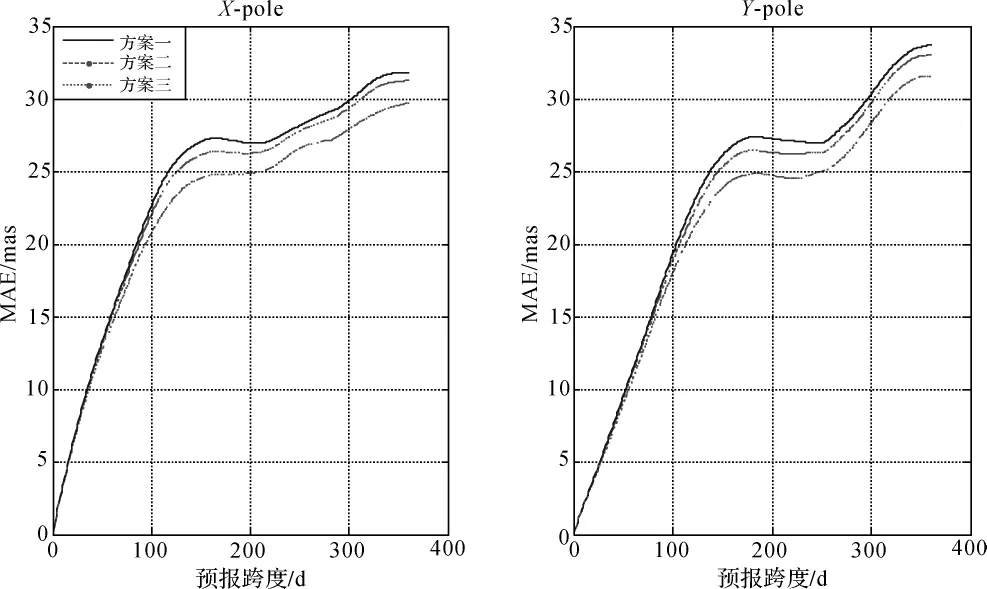
图2 方案一、二、三预报精度对比

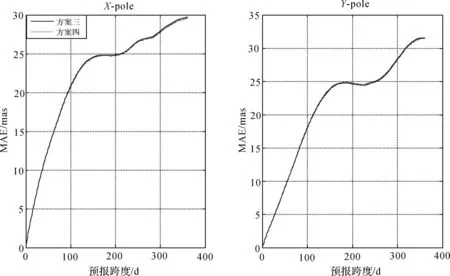
图3 方案三、四预报精度对比

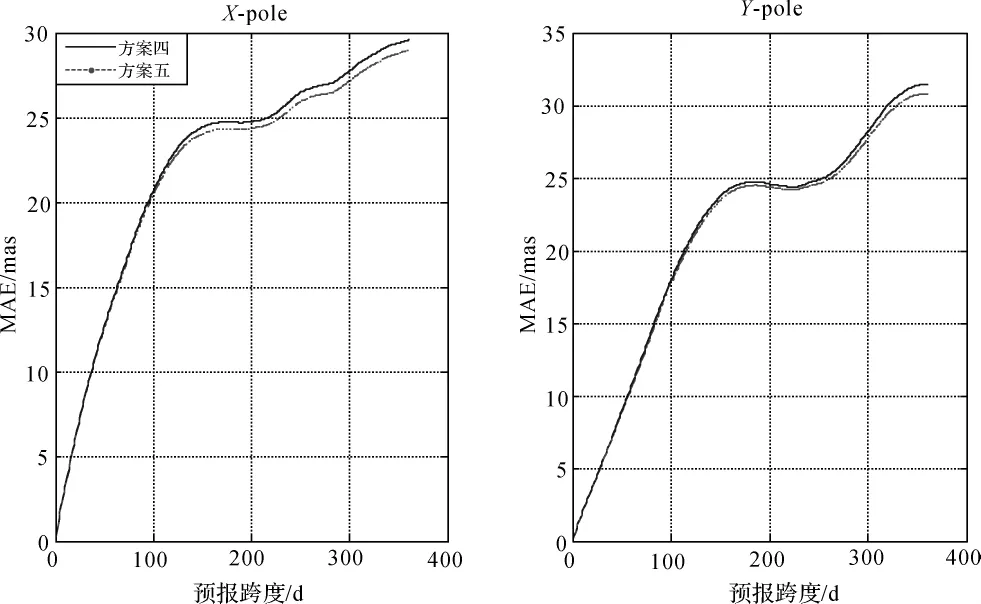
图4 方案四、五预报精度对比

四、结束语

本文基于LS+AR预测模型对极移进行高精度的预报，由于在极移数据中其周年项、钱德勒项等周期项具有时变性的特点，并不是只局限于某些具体的数值，故在预报之前首先对极移数据做频谱分析，确定出所应用观测数据中的最优周年项和钱德勒项数值，然后应用所确定的具体数值来进行最小二乘的拟合进而预报未来极移数据，通过此种方法预报的极移精度要比以往国内外学者应用同种方法的具体周期数所得的预报精度都要高，因此，建议在进行地球定向参数预报之前，应首先确定所用数据的具体周期频谱值，在极移预报中加以考虑，可进一步提高预报的精度和可靠性。

[1]郑大伟，虞南华．地球自转及其地球物理现象的联系：I日长变化[J]．地球物理学进展，1996，11(2)：81-101．

[2]AKYILMAZ O，KUTTERER H．Prediction of Earth Rotation Parameters by Fuzzy Inference Systems[J]．Journal of Geodesy，2004(78)：82-93．

[3]SCHUH H，ULRICH M，EGGER D，et al．Prediction of Earth Orientation Parameters by Artificial Neural Networks[J]．Journal of Geodesy，2002(76)：247-258．

[4]KOSEKW，KALARUSM，NIEDZIELSKIT．Forecasting of the Earth Orientation Parameters—Comparison of Different Algorithms[C]∥ Proceedings of the Journèes 2007，SystèMes De Référence Spatio-temporels“The Celestial Reference Frame for the Future”．Paris：[s．n．]，2007：155-158．

[5]KOSEKW．Future Improvements in EOP Prediction[C]∥Proceedings of the IAG 2009，“Geodesy for Planet Earth”．Argentina：[s．n．]，2009．

[6]KOSEK W．Causes of Prediction Errors of Pole Coordinates Data[C]∥Proceedings of the 6th Orlov’s Conference，“The Study of the Earth As a Planet by Methods of Geophysics，Geodesy and Astronomy”Ukraine：[s．n．]，2009：96-103．

[7]KALARUSM，SCHCH H，KOZEK W，et al．Achievements of Earth Orientation Parameters Prediction Comparison Campaign[J]．Journal of Geodesy，2010(84)：587-596．

[8]SCHUH H，NAGEL S，SEITZ T．Linear Drift and Periodic Variations Observed in Long Time Series of Polar Motion[J]．Journal of Geodesy，2001(74)：701-710．

[9]王琪洁．基于神经网络技术的地球自转变化预报[D]．上海：中国科学院上海天文台，2007．

[10]XU X Q，ZHOU Y H，LIAO X H．Short-term Earth O-rientation Parameters Predictions by Combination of the Least-squares，AR Model and Kalman Filter[J]．Journal of Geodynamics，2011(1107)：4．

[11]张昊，王琪洁，朱建军，等．加权最小二乘法与AR组合模型在极移预测中的应用研究[J]．天文学进展，2011，29(3)：343-352．

[12]KOSEK W，MCCARTHY D D，LUZUM B J．El Nino Impact on Polar Motion Prediction Errors[J]．Stadia Geophysica et Geodaetica，2001(45)：347-361．

[13]DENNISDM，BRIAN JL．Prediction of Earth Orientation[J]．Journal of Geodesy，1991(65)：18-21．