基于RBF神经网络的GPS精密星历卫星坐标插值

陶庭叶，李晓莉，高 飞

(合肥工业大学土木与水利工程学院，安徽合肥230009)

一、引 言

利用GPS导航定位，必须要计算出卫星在相应时刻的坐标，而卫星的坐标主要是通过星历得到的。星历分为广播星历与精密星历两种。广播星历可直接从GPS的导航电文中获得;精密星历则由发布获得，目前有多家机构发布精密星历，这些星历是利用全球分布的永久GPS跟踪站数据计算得到的。精密星历分为事后星历与预报星历，其精度分别为±0．05m与±0．2m左右。精密星历一般以SP3格式发布。目前，IGS及其数据分析中心发布的最终精密星历(SP3格式)的采样间隔为15 min，IGS及其一些数据分析中心则相继发布了间隔更密(如5min和30 s)的精密卫星钟差数据产品。对于时间间隔内任意时刻的卫星坐标一般采用多项式拟合或拉格朗日等插值法内插求出，其对内插的要求是不能明显损失原始星历的精度。因此，高精度、快速实现对精密星历和钟差参数的插值或拟合就成为了GPS数据处理中一项重要的工作[1-6]。

目前，DMA[7]、NGS[8]、JPL 等机构常用的内插方法是8到11阶(或9到12阶)Lagrange多项式插值。其结果表明，对于15 min间隔数据，在数据中间部分，8阶 Lagrange多项式插值的精度可达±1 cm。Schenewerk对插值方法作了简单的总结，文章研究表明，Lagrange多项式、Chebyshev多项式等类型多项式插值精度相当，三角函数插值精度略好。这些方法基本都能够得到较好的精度[9]。但是，多项式插值的方法存在着一个问题，那就是Runge现象(runge phenomenon，RP)。所谓RP是指随着插值多项式阶数升高，在插值区间的两端出现振荡现象，从而导致两端的插值精度急剧下降，需要采取分段滑动拟合或减小步长等方法来减小其影响，但是，这种方法会增加计算开支[10]。

针对利用多项式对卫星坐标插值出现Runge现象的问题，本文提出了利用RBF神经网络对卫星坐标进行插值的方法，并通过试验验证了该方法对精密星历卫星坐标插值的计算具有高效性、高精度与通用性的特点。

二、RBF神经网络插值与拟合原理

1．RBF 神经网络[11-12]

1985年，Powell提出了多变量插值的径向基函数(radial basis function，RBF)方法。1988年Broomhead和Lowe首先将RBF应用于神经网络设计，从而构成了RBF神经网络。RBF神经网络具有逼近非线性函数能力强和网络收敛速度快的优点。

RBF网络的结构与多层前向网络类似，它是一种3层前向网络。第1层为输入层，由信号源结点组成;第2层为隐含层，隐单元数视所要描述的问题而定;第3层为输出层，它对输入模式的作用作出响应。从输入控件到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间变换是线性的。由输入层、隐含层和输出层构成的一般径向基神经网络结构如图1所示。

RBF网络的关键在于隐含层节点径向基函数的非线性逼近性能，一般采用的RBF函数是Gauss分布函数，即隐含层节点k的传递函数表达式为

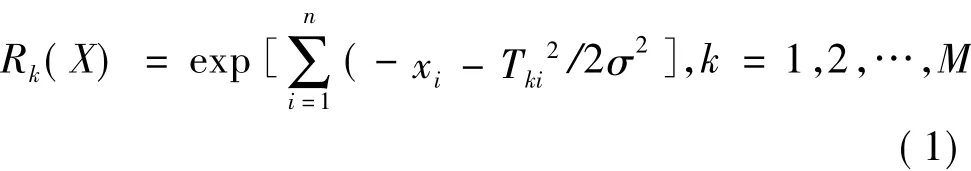
式中，X=(xi|i=1，2，…，n)，n 为输入向量;Tki为节点k的中心Tk的第i个分量;σk为节点k的Gauss分布宽度;‖·‖表示欧式范数。

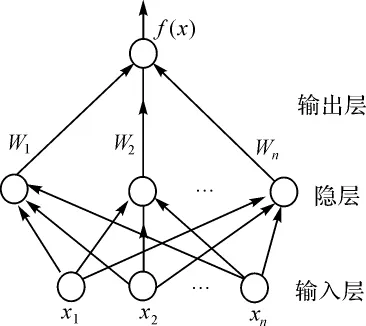
图1 径向基神经网络结构

输出层节点相应的输出则可以表示为

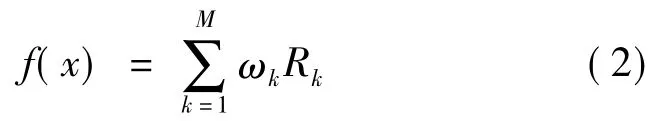
RBF神经网络的学习算法为：随机选取h个训练样本作为聚类中心ci(i=1，2，…，h)，将输入的训练样本集合按最近邻规则分组，计算各个聚类集合中训练样本的平均值，即新的聚类中心，如果新的聚类中心不再发生变化，则所得到的聚类中心即为RBF网络的聚类中心。

RBF神经网络的基函数为高斯函数，因此方差σi可由下式求解

式中，cmax为所选取中心之间的最大距离。

应用最小二乘法对网络输出权值进行训练，其学习训练的目标是使总误差达到最小。

RBF神经网络实现的是非线性映射(横向滤波器只作线性映射)。目前，从理论上已经证明，只要隐含层神经元数足够多，RBF神经网络可以任意精度逼近任何单值连续函数[13]。

2．RBF神经网络插值

插值问题的提法为：给定区间上N个点xi(i=1，…，N)及其对应的函数值 yi(i=1，…，N)，要求构造一元函数y=f(x)在N个点处满足给定的函数值，即 f(xi)=yi(i=1，…，N)。

采用RBF神经网络进行插值的具体算法如下：

1)将输入数据xi(i=1，…，N)作为样本集，将yi(i=1，…，N)作为输出集;

2)计算各样本的聚类中心;

4)采用上述RBF神经网络进行插值。

三、基于RBF神经网络GPS卫星坐标插值试验与结果分析

本文利用RBF神经网络拟合精密星历的卫星坐标，在保证精度的前提下，要避免高阶多项式拟合出现的RP现象，同时，要保证本方法的计算效率。基于这一点，设计以下试验方案。

方案1：对于不同长度的时间段，分析RBF神经网络对卫星坐标插值效果。

方案2：对于不同的卫星，分析RBF神经网络对所有32颗GPS卫星坐标插值效果。

方案3：同时采用RBF神经网络对同一组卫星坐标进行拟合，在精度相当的情况下，比较二者所耗费计算时间差异。

1．方案1试验结果及分析

采用IGS提供的15min间隔星历的卫星坐标，选用 PG01号卫星2010年11月 7日 00：00：00—00：03：00、00：00：00—00：04：00、00：00：00—00：05：00与00：00：00—00：06：00 4 个不同长度时间段数据。抽取30min间隔数据进行拟合，利用RBF神经网络插值得到15min间隔星历数据，将插值结果与真实坐标进行比较，求出插值残差，利用插值残差绝对值的最大值(MAX)与标准差(SD)衡量插值精度。

表1为3个时间段插值结果。

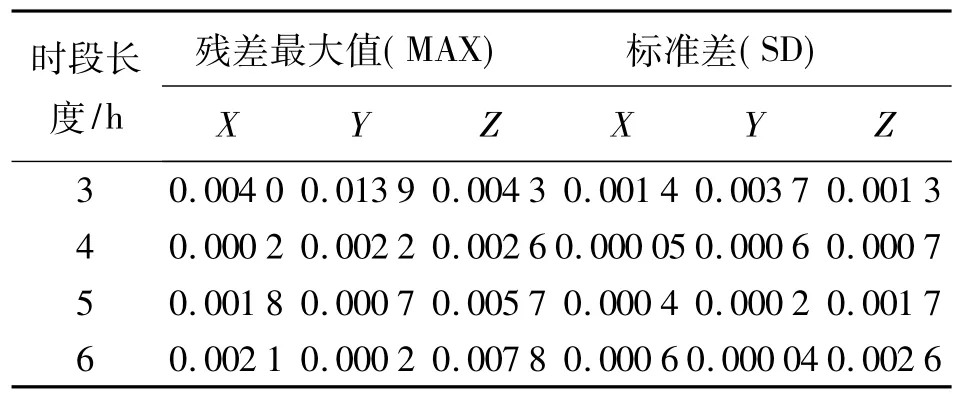
表1 不同长度时间段插值残差 m

从表1可以看出，利用RBF神经网络对不同时间段的精密星历拟合效果比较好，残差标准差都在毫米级以内，有的达到亚毫米级甚至更好。在拟合时间段4～5 h的情况下，拟合效果最佳，拟合残差最大值在2mm左右，但随着拟合时间段变短或者变长，插值效果逐步变差。这是由于随着拟合时间段增加，星历间的相关性逐渐下降，导致插值效果变差，而插值时间段过短，参与神经网络建模的样本数据较少，模型效果也相应变差。

2．方案2试验结果及分析

同样采用IGS提供的15 min间隔星历的卫星坐标，选用PG01—PG32号卫星共32颗2010年11月7 日 00：00：00—00：04：00 共 4 个小时数据。抽取30min间隔数据进行拟合，利用RBF神经网络插值得到15min间隔星历数据，将插值结果与真实坐标进行比较，求出插值残差，并采用插值残差绝对值的最大值(MAX)与标准差(SD)来衡量插值精度。

图2表示每个时间段每个卫星三维坐标插值残差的最大值与标准差。

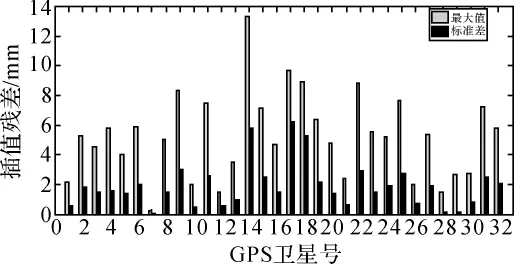
图2 32颗卫星星历拟合残差最大值与标准差

从图2可以看出，采用RBF神经网络，几乎所有卫星的精密星历卫星坐标插值残差的最大值都在1 cm以内，只有14号卫星插值残差的最大值超过1 cm，达到1．33 cm，但这只是在个别历元上，在各个历元拟合残差的标准差为5．4mm，小于1 cm，这说明该卫星星历总体插值效果良好。由此可知，利用RBF神经网络插值方法对于所有卫星的精密星历卫星坐标插值效果良好，即使在个别卫星、个别历元处于最不理想的状况，其插值残差最大值也能达到1 cm左右，不会使得精密星历精度明显下降，能够满足各类定位要求。

3．方案3试验结果及分析

同样采用IGS提供的15 min间隔星历的卫星坐标，选用PG01号卫星2010年11月7日00：00：00-00：04：00时间段数据。抽取30 min间隔数据进行拟合，分布采用Lagrange多项式插值与RBF神经网络插值得到15min间隔星历数据，将插值结果与真实坐标进行比较，求出拟合差值，采用插值残差绝对值的最大值(MAX)与标准差(SD)衡量插值精度，在二者插值精度相当时比较二者耗费的CPU时间。

采用RBF神经网络插值，X方向的插值残差最大值与标准差分别为0．2mm与0．05mm，插值所耗费CPU时间为4．765 6 s。

同一数据采用Lagrange插值效果如图3所示。图3中出现了Runge现象，两端的插值误差达到2 cm以上，中间部分插值效果良好，X方向插值残差最大值与标准差分别为5．8mm与2．8mm，每个所耗费CPU时间为5．359 4 s。

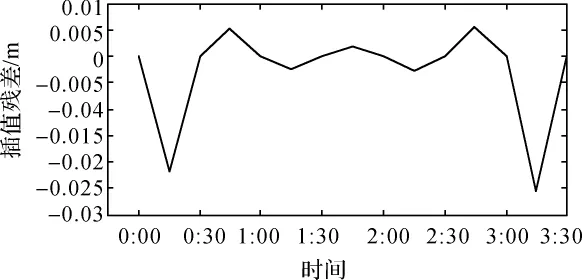
图3 X方向数据Lagrange插值效果图

这说明，采用RBF神经网络对精密星历进行插值在保证插值精度能够达到多项式插值的前提下，插值所耗费的计算时间略优于Lagrange插值。这就可以证明采用RBF神经网络进行精密星历卫星坐标插值兼顾了插值精度与计算效率。

四、结 论

根据所设计的不同方案，采用RBF神经网络对IGS精密星历所提供的GPS卫星坐标进行了拟合插值，结果表明：

1)RBF神经网络对于长度为3～6 h时间段的GPS卫星坐标插值残差的标准差均在毫米级甚至更好，不会降低IGS星历提供的卫星坐标本身的精度，对4 h时间段GPS卫星坐标拟合效果最佳。

2)RBF神经网络对于所有GPS卫星坐标插值残差的标准差均在毫米级甚至更好，说明该方法对于GPS卫星坐标插值拟合具有通用性。

3)RBF神经网络对于GPS卫星坐标插值避免了一般多项式插值在多项式阶数达到一定程度时出现RP现象，保证所有插值时刻都能达到相应的精度。

4)RBF神经网络对于GPS卫星坐标插值在保证精度的前提下，在计算效率方面不输于多项式插值。

[1]HOREMUŽM，ANDERSSON JV．Polynomial Interpolation of GPS Satellite Coordinates[J]．GPS Solutions，2006(10)：67-72．

[2]刘迎春，林宝军，张晓坤．一种卫星精密星历的插值方法[J]．飞行器控制学报，2004，23(4)：43-46．

[3]蔡艳辉，程鹏飞，李夕银．卫星坐标的内插和拟合[J]．全球定位系统，2003，28(3)：10-13．

[4]洪樱，欧吉坤，彭碧波．GPS卫星精密星历和钟差三种内插方法的比较[J]．武汉大学学报：信息科学版，2006，31(6)：516-518．

[5]李征航，黄劲松．GPS测量与数据处理[M]．武汉：武汉大学出版社，2005．

[6]张守建，李建成，邢乐林，等．两种IGS精密星历插值方法的比较分析[J]．大地测量与地球动力学，2007，27(2)：80-83．

[7]MALYS S，ORTIZ M J．Geodetic Absolute Positioning with Differenced GPS Carrier Beat Phase Data[C]∥Proceedings of the 5th International Symposium on Satellite Positioning，Las Cruces：[s．n．]，1989．

[8]REMONDI B W．NGS Second Generation ASCII and Binary Orbit Formats and Associated Interpolation Studies[C]∥ Poster Session Presentation at the 20th generalassembly of the IUGG，Vienna：[s．n．]，1991．

[9]SCHENEWERK M．A Brief Review of Basic GPSOrbit Interpolation Strategies[J]．GPS Solutions，2003(4)：265-267．

[10]FENG Yanming，ZHENG Yi．Efficient interpolations to GPS Orbits for Precise Wide Area Applications[J]．GPSSolutions，2005(4)：273-282．

[11]ROBERT H N．Theory of the Back-propagation Neural Network[J]．UCNN，1989(1)：593-605．

[12]HINT K J．Extending the Functional Equivalence of Radial Basis Function Network and Fuzzy Inference System[J]．IEEE Trans on Neural Networks，1996(3)：776-781．

[13]杨行峻，郑君里，人工神经网络与盲信号处理[M]．北京：清华大学出版社，2002．