非对称笼间电子迁移异构体与电场诱导电子迁移

王银锋 黄俭根 周光培 李志儒

(1井冈山大学化学化工学院,应用化学研究所,江西省配位化学重点实验室,江西吉安343009; 2吉林大学理论化学研究所,理论计算化学国家重点实验室,长春130023)

非对称笼间电子迁移异构体与电场诱导电子迁移

王银锋1,*黄俭根1周光培1李志儒2,*

(1井冈山大学化学化工学院,应用化学研究所,江西省配位化学重点实验室,江西吉安343009;2吉林大学理论化学研究所,理论计算化学国家重点实验室,长春130023)

基于密度泛函理论研究了非对称双笼型单分子溶剂化电子e-@C24F22(NH)2C20F18(1、2和3),进一步展示了我们提出的一种新型电子异构体——(非对称型的)笼间电子迁移异构体.1、2和3具有显著不同的偶极矩.由于都存在两个氧化还原中心,它们属于一种非金属型的新型Robin-Day II-III分子.对于1和3,额外电子分别定域在C24F22和C20F18笼里(Robin-Day II);对于2,额外电子则离域于两个非对称的笼中(Robin-Day III).值得注意的是,在y轴方向上外加-0.0004和-0.0008 a.u.的临界电场(Ec)时可分别使1的额外电子从C24F22笼中部分和全部地迁移到C20F18笼中,即实现从1到2再到3的转化;当Ec为0.0004 a.u.时,3的额外电子从C20F18笼中全部迁移到了C24F22笼中,即3未经过2直接转化成了1.

电场诱导;Robin-Day分子;单分子溶剂化电子;电子异构体;不对称笼间电子迁移

1 引言

同分异构体是化学里一个非常重要的概念,随着时代的发展,它所包括的内容越来越广泛.1已知的各种异构体主要可分为构造异构体和立体异构体,后者又可分为非对映异构体(顺反异构体和构象异构体等)及对映异构体.1这些异构体属于分子层面的范畴,可称为分子异构体.最近,一类新的异构体——电子异构体(electromer)吸引了越来越多的关注.2-7电子异构体之间在几何结构上差别不大,但在电子结构上却具有显著的差异.1,2已经报道的三类电子异构体包括价异构体(或氧化还原异构体)、3-5自旋异构体1和组态异构体.6,7价异构体一般由氧化还原配体和具有多种价态的过渡金属构成.2自旋异构体常常涉及到电子激发问题.1Tian6和Lu7等报道了一些由于最高占据轨道(HOMO)和最低空轨道(LUMO)之间相互转化而形成的组态异构体.

混价化合物是其中某种元素的几个原子具有不同原子价(A价和B价)的一类化合物.混价化合物的研究已成为一门跨学科的前沿性研究课题.8随着人们对混价化学认识的不断深入以及它在颜料、陶瓷、矿物、生物体系及超导材料等方面独特的作用,该领域的研究已越来越引起人们的兴趣.8Robin和Day9以及其他研究者8,10总结了混价体系的化学性质,并依据配位场理论把各种混价化合物归纳为三类:第I类中处于A和B两种不同价态的离子具有不同的配位环境和对称性;第II类含有部分离域键的性质,处于不同价态的金属离子通常具有相近的配位环境;第III类中,A态和B态之间含有非常强的离域键,处于两状态的金属离子具有完全相同的配位环境和对称性.混价化合物也称为Robin-Day分子.最近,Meyer等11研究了由第II类(定域)到第III类(离域)过渡的情况.对于价间电荷迁移系统,基于纯有机物种的且处于第II-III类过渡区域的新型给体-受体体系已经被报道.12

溶剂化电子的研究在物理、化学和生物化学领域起着重要的作用.13被束缚着的额外电子的稳定和控制对于分子团簇和纳米器件来说非常重要,14并有助于制备具有独特的光学性质或磁学性质的传导材料.15,16使用全氟化的碳笼束缚额外电子,我们得到了一系列单分子溶剂化电子体系,其中包括单笼型的e-@C60F60、e2@C60F60和双笼型的e-@C20F18(NH)2C20F18、e-@C24F22(NH)2C20F18.17-20相对于溶剂化的分子团簇,由于共价碳笼的存在,我们得到单分子溶剂化电子体系具有更大的稳定性.17最近,Wang和Ma21采用e-@C20F18(NH)2C20F18构造了新型的量子点细胞自动机(molecular quantum-dot cellular automata).对于得到的双笼型的单分子溶剂化电子体系,笼间的额外电子迁移涉及的是基态势能面和第一激发态势能面.19那么,在基态势能面上,e-@C20F18(NH)2C20F18或e-@C24F22(NH)2C20F18的额外电子是否可占据于不同的笼子?由于两个笼子各存在着一个氧化还原中心,若额外电子存在着不同的占据,一种新的非金属型的Robin-Day分子将形成,同时一种新型的有趣的笼间电子迁移异构现象也将产生.

我们20最近的研究显示,含有对称笼子(C20F18)的e-@C20F18(NH)2C20F18的基态存在这种新型的笼间电子迁移异构体.既然如此,那对于含不对称笼子(C24F22和C20F18)的e-@C24F22(NH)2C20F18来说,笼子的不同会让额外电子的不同占据还表现出稳定性吗? Li等22的研究显示,当外加电场达到一个临界值时,可发生HCl→NH3(H2O)的质子迁移,从而使氢键向离子键转变.我们的研究也显示适当的外加电场可使对称的e-@C20F18(NH)2C20F18产生笼间额外电子迁移而发生异构化.20若非对称型的笼间电子迁移异构体存在,那么笼子的非对称性对异构体的结构、稳定性及偶极矩等性质会有什么影响?当给予非对称的e-@C24F22(NH)2C20F18一个适当的外加临界电场时也会产生笼间额外电子迁移而发生异构化吗?两笼子(C24F22和C20F18)的不对称性对临界电场的大小和额外电子的迁移有什么影响?这些都是值得研究的问题.

本文的研究目的在于得到非对称型笼间电子迁移异构体e-@C24F22(NH)2C20F18的结构、稳定性、偶极矩及非对称性对它们的影响,揭示外加临界电场诱导下不对称笼间额外电子迁移的本质,拓展异构化与额外电子化学的相关知识.

2 计算模型和方法

Jordan23和Simons24等建议采用弥散基函数去描述额外电子的弥散特征.我们的研究显示B3LYP/ 6-31G(d)+4s4p方法能够很好地得到一系列的单分子溶剂化电子结构.17-20因此,e-@C24F22(NH)2C20F18的不同异构体(1、2和3,图1)的几何优化和频率计算也采用B3LYP/6-31G(d)+4s4p方法得到.根据Simons等24的建议,本文4s4p弥散基函数来自于对碳原子6-31G(d)基组的最低指数(s和p,0.1687144)的修改,包括以下4个s和4个p弥散轨道:s(0.1687144), s(0.01687144), s(0.001687144), s(0.0001687144), p(0.1687144),p(0.01687144),p(0.001687144)和p(0.0001687144).为了得到e-@C24F22(NH)2C20F18的不同异构体(1、2和3),1和3的4s4p弥散基函数分别放在C24F22(左边)和C20F18(右边)笼子的中心,2的4s4p弥散基函数放在两个N原子的中心.考虑到DFT方法的可靠性,我们采用HF/6-31G(d)+4s4p方法(自旋角动量的平方＜s2＞=0.75)得到的2的优化几何同样具有全部的实频,这说明B3LYP/6-31G(d)+ 4s4p方法的计算是可靠的.

许多文献一直在争论密度泛函理论(DFT)是否可以产生可靠的电子亲和势(EAs)或垂直电离势(VDE).17,25-27我们的计算显示含长程相关效应的LC-BLYP方法28对于溶剂化电子体系e2@(LiF)6的VDE计算能更好地接近二级微扰理论(MP2)的结果.19,20,29因此,基于下列公式,1、2和3的VDE和 VEA(垂直电子亲和势)均采用LC-BLYP/6-311++ G(d,p)+6s6p4d方法得到.

图1 e-@C24F22(NH)2C20F18的不同异构体的结构、单占据分子轨道(SOMOs)(等值面:0.035 a.u.)和自旋密度分布(等值面:0.001 a.u.)Fig.1 Structures,single occupied molecular orbitals (SOMOs)(at the isovalue of 0.035 a.u.),and spin densities (at the isovalue of 0.001 a.u.)of inter-cage electron-transfer isomers of e-@C24F22(NH)2C20F18

其中,E[M]、E[M-]和E[M2-]分别表示C24F22(NH)2-C20F18、e-@C24F22(NH)2C20F18和 e2-@C24F22(NH)2C20F18的能量,三者的结构均来自于e-@C24F22(NH)2C20F18. 6s6p4d同样来自于对碳原子6-31G(d)基组的最低指数(s和p,0.1687144)的修改.24它包括以下6个s和6个p以及4个d弥散轨道,s(0.0438),s(0.00876), s(0.001752), s(0.0003504), s(0.00007008), s(0.000014016),p(0.0438),p(0.00876),p(0.001752), p(0.0003504), p(0.00007008), p(0.000014016), d(0.626),d(0.1252),d(0.02504)和d(0.0050080).经检查,可忽略所有计算产生的自旋污染.

额外电子吸收光谱采用单激发组态相互作用方法(CIS)和6-31G(d)基组计算得到,考虑到CIS和Hartree-Fock(HF)对基态偶极矩计算结果相同,体系的基态和第一激发态的偶极矩也采用CIS/ 6-31G(d)方法得到.全部的计算采用Gaussian 09程序包.30

3 结果与讨论

3.1 非对称型的笼间电子迁移异构体

图1给出了B3LYP/6-31G(d)+4s4p水平下的非对称型的e-@C24F22(NH)2C20F18的笼间电子迁移异构体1、2和3的结构.它们的几何构型几乎相同,即均具有两个不同的氟化碳笼(C24F22和C20F18),两个笼子采用NH桥连.结构数据见表1,从表1可看出C24F22和C20F18的尺寸大小顺序均是:带有额外电子的笼子(1的L1和d1或3的L2和d2)＜带有部分电子的笼子(2的L1和d1或L2和d2)＜不带有额外电子的笼子(3的L1和d1或1的L2和d2).这些说明额外电子的存在稍微减少了氟化碳笼的尺寸.1、2和3间的相应参数(d或L)的差值小于0.3 nm.因此,异构体1、2和3结构上的差异非常小.

表1 B3LYP/6-31G(d)+4s4p水平上计算得到不同异构体的结构参数Table 1 Structural parameters of different isomers calculated at the B3LYP/6-31G(d)+4s4p level

图1也分别给出了1、2和3的单占据分子轨道(SOMO)及自旋密度分布.图中的s型电子云及相应的自旋密度分布均说明1和3的额外电子分别占据在左边的C24F22和右边的C20F18笼子里,而2的额外电子则离域于两个非对称的笼子中.为验证异构体2的可靠性,采用HF/6-31G(d)+4s4p方法(＜s2＞=0.75)的结构优化同样显示额外电子离域在两个非对称的笼子里.虽然1、2和3具有几乎相同的几何结构,但却具有明显不同的电子结构.因此,1、2和3是一种新型非对称笼间电子迁移异构体.

e-@C24F22(NH)2C20F18的每个异构体都由一个C24F22和C20F18笼子构成.由于C和F具有明显不同的电负性,形成的外接(exo)C－F键在每个笼心产生了很强的内部电子吸引势.17这使每个异构体都存在两个氧化还原中心.因此,1、2和3也是一种非金属型的新型混价分子(Robin-Day II-III).8由于额外电子分别定域在C24F22和C20F18笼子里,1和3是第二类混价分子(Robin-Day II);由于额外电子离域在两个非对称的笼子里,2是第三类混价分子(Robin-Day III).左右氟化碳笼的中心由于额外电子的占据而形成的化合价分别为-1和0(1),-0.58和-0.42 (2),0和-1(3).其中2的笼心的化合价来自于2的C24F22和C20F18笼的Mulliken电荷比值(见Supporting Information中图S1).

3.2 稳定性

比较1、2和3相对能量,表2显示在LC-BLYP/ 6-311++G(d,p)+6s6p4d水平上,2和3的总能量(Etot)分别要比1高出64.00和49.53 kJ·mol-1;而在B3LYP/6-311++G(d)+4s4p水平上,2和3的总能量分别要比1仅仅高出8.06和3.32 kJ·mol-1,经过零点能校正后,2和3的总能量分别要比1高出30.35和13.25 kJ·mol-1.这些说明虽然1是热力学最稳定的异构体,但是1、2和3的热力学稳定性差异并不大.

根据分子轨道分析,最高占据轨道(HOMO)和最低空轨道(LUMO)的能量间隙(Egap)可作为动力学稳定性的一个简单标识.31这个能量间隙越大,则动力学稳定性越大;相应地,化学还原性就越小.由表2可知Egap的顺序是3.827 eV(1)＞3.626 eV(2)＞3.426 eV(3),这说明1、2和3的动力学稳定性是逐渐减小的.

采用LC-BLYP/6-311++G(d,p)+6s6p4d方法得到的1、2和3的VDE和VEA也列在表2里.对于e-@C24F22(NH)2C20F18来说,小的VDE说明容易抽出SOMO上的额外电子,即易被氧化;而大的VEA则暗示增加一个额外电子到SOMO轨道上时将释放出大的能量,即易于被还原.1、2和3的VDE分别是4.032、3.929和3.840 eV.非对称性的e-@C24F22(NH)2C20F18的各个异构体的VDE值分别比对称性的异构体的相应值(3.660 eV(1)、3.324 eV(2)和3.660 eV(3))20要大.因此,非对称性的e-@C24F22(NH)2C20F18的各个异构体分别比对称性的e-@C20F18(NH)2C20F18的相应异构体难于氧化.同时,1、2和3的VDE值均比稳定的水合电子负离子团簇(H2O)的极限VDE值(3.3 eV)要大,32也就是说它们的还原能力要比稳定的水合电子负离子团簇的还原能力要小,即前者更稳定.我们的计算显示,当增加一个额外电子到1的SOMO或者LUMO时,三态结构的能量要比单态结构的能量要低,即VEA(s)＜VEA(t)(见表2).同时,B3LYP/6-31G(d)+4s4p优化得到的e2-@C24F22(NH)2C20F18结 构 显 示,三 态 的 能 量(-5780.5789 a.u.)比单态(-5780.5718 a.u.)的要低.因此,我们只计算了1、2和3的VEA(t)来进行比较.从表2可以看出1、2和3的氧化性是逐渐增大的.

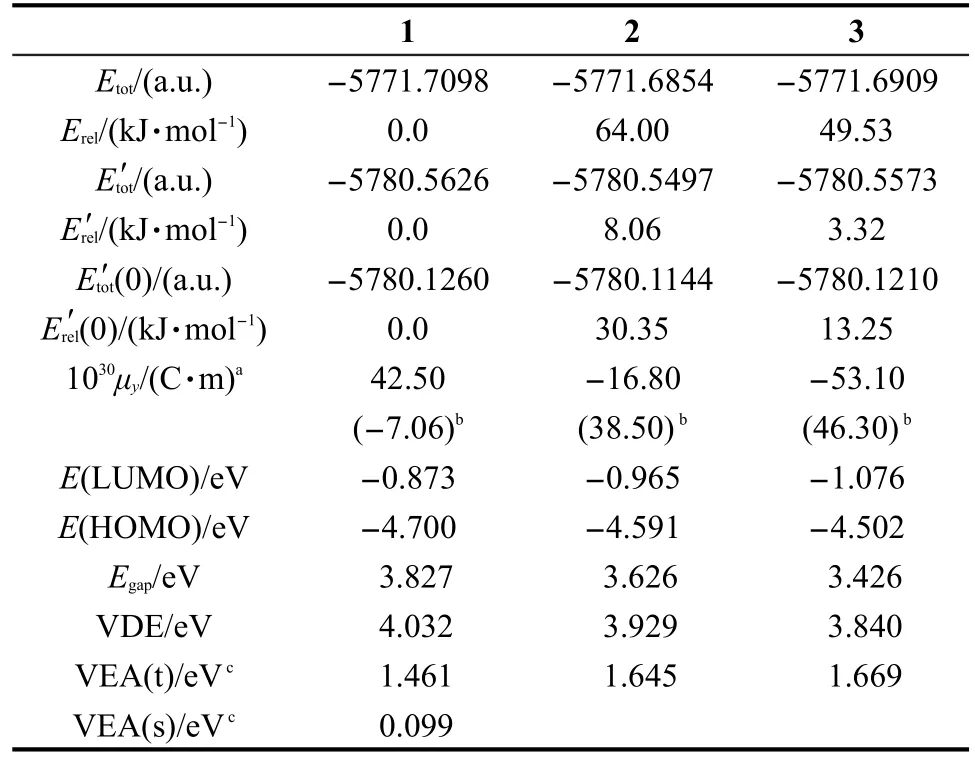
表2 计算得到的体系能量值、偶极矩、垂直电离势和电子亲和势Table 2 Calculated energies,dipole moments,VDEs,and VEAs of the systems

因此,不管是在热力学上还是动力学上,1在三个异构体中都是最稳定的.这说明额外电子更喜欢占据在大笼子里.计算得到的1、2和3的红外光谱显示在Supporting Information的图S2里.

3.3 额外电子吸收光谱与偶极矩

图2给出了异构体1、2和3的额外电子吸收光谱.由于额外电子的不同定位,1、2和3具有明显不同的吸收光谱.在低频区域,1、2和3分别具有4个振子强度较大(f0＞0.04)的吸收峰.随着额外电子从定位于左边C24F22笼向右边C20F18笼的转移,即从1到2再到3,低频区域的吸收峰特别是第一吸收峰先发生蓝移再发生红移,同时其振子强度也先减弱后又增强.图3给出了低频区的吸收峰的相应的能级图和轨道图.对于1、2和3来说,从基态到第一激发态的跃迁是笼内或笼间的s→s型轨道跃迁,而从基态到第二及以上的激发态的跃迁是笼内或笼间的s→p型轨道跃迁.值得注意的是,从基态到第一激发态1和3均发生的是笼间的额外电子迁移,也就是说1或3的第一激发态的额外电子定位恰好分别和3或1的基态的额外电子定位是一致的.因此,把1和3的额外电子分别从基态激发到第一激发态,然后经过一个无辐射的迁移就可实现1和3笼间额外电子的迁移,即实现1和3之间的异构化.

在CIS/6-31G(d)水平上,表2显示1、2和3的偶极矩在y轴上的分量(μy)在基态分别是4.25×10-29C· m(1),-1.68×10-29C·m(2)和-5.31×10-29C·m(3),这说明不同的额外电子定位导致了明显不同的偶极矩;同时,1、2和3的μy在第一激发态分别是-7.06×10-30C·m(1),3.58×10-29C·m(2)和4.63× 10-29C·m(3).这说明从基态到第一激发态的笼间或笼内的额外电子迁移使得1、2和3的偶极矩发生了显著的变化.

1的μy的方向是从C24F22的笼心指向C20F18的笼心,3的μy的方向是从C20F18的笼心指向C24F22的笼心.一般情况下,极性C－F键越多,笼心的电负性就越大,因此2的μy方向应从具有较多极性C－F键的C24F22的笼心指向具有较少极性C－F键的C20F18的笼心.事实上,2的μy方向并不是从C24F22的笼心指向C20F18的笼心,而是从C20F18的笼心指向了C24F22的笼心.值得注意的是,表1显示C24F22笼的尺寸要比C20F18笼的尺寸大,更重要的是C24F22笼的对称性明显弱于C20F18的对称性.因此C24F22虽然有更多的C－F键,但是它的偶极矩反而可能更小.为了验证这一点,我们从1和3中分别截取了占据额外电子的C24F22和C20F18笼,并补充F原子做成了C24F24和C20F20笼的模型.在CIS/6-31G(d)方法下的计算显示C24F24和C20F20笼的μy值大小分别是3.85×10-31和9.09×10-31C·m.这些说明并不是具有较多极性CF键的C24F22的笼心的电负性比具有较少极性C－F键的C20F18的笼心的电负性大,而是后者的电负性较前者大.因此,2的μy方向并不是从C24F22的笼心指向C20F18的笼心而是从C20F18的笼心指向了C24F22的笼心.同时,从绝对值的比较来看,3的μy的绝对值(5.31×10-29)要稍大于1的μy的绝对值(4.25×10-29)也是由于这个原因.

3.4 非对称笼间电子迁移异构化

对于异构体1、2和3,它们之间的异构化是值得注意的.图3显示1和3之间的异构化可通过把额外电子从基态激发到第一激发态,然后经过一个无辐射的迁移就实现.

图2 1(a),2(b)和3(c)的额外电子吸收光谱Fig.2 Excess electronic absorption spectra for 1(a),2(b),and 3(c)f0:oscillator strength

图4显示当外加电场在y方向上(Fy)的临界值(Ec)为-0.0004和-0.0008 a.u.时可分别使具有非对称性的氟化碳笼的e-@C24F22(NH)2C20F18的1的额外电子从C24F22笼部分和全部地迁移到C20F18笼中,即实现了从1到2和3的单向转化,这和对称性e-@C20F18(NH)2C20F18的情况比较相似,只是Ec数值降低了;当Ec为-0.0004 a.u.时,e-@C24F22(NH)2C20F18的2的C24F22笼中的部分额外电子全部地迁移到了C20F18笼中,即实现了从2到3的单向转化,这类似于e-@C20F18(NH)2C20F18的情况,同样是Ec的数值降低了;当Ec小于0.0004 a.u.时,3的额外电子始终占据于C20F18笼中,当Ec为0.0004 a.u.时,3的额外电子从C20F18笼全部迁移到了C24F22笼中,即3没经过2直接转化成了1.当也就是说,在外加临界电场作用下,笼子的非对称性使得e-@C24F22(NH)2C20F18发生了和对称性的e-@C20F18(NH)2C20F18相似的1→2→3笼间额外电子迁移,但却并没有发生相似的3→2→1笼间额外电子逆向迁移.

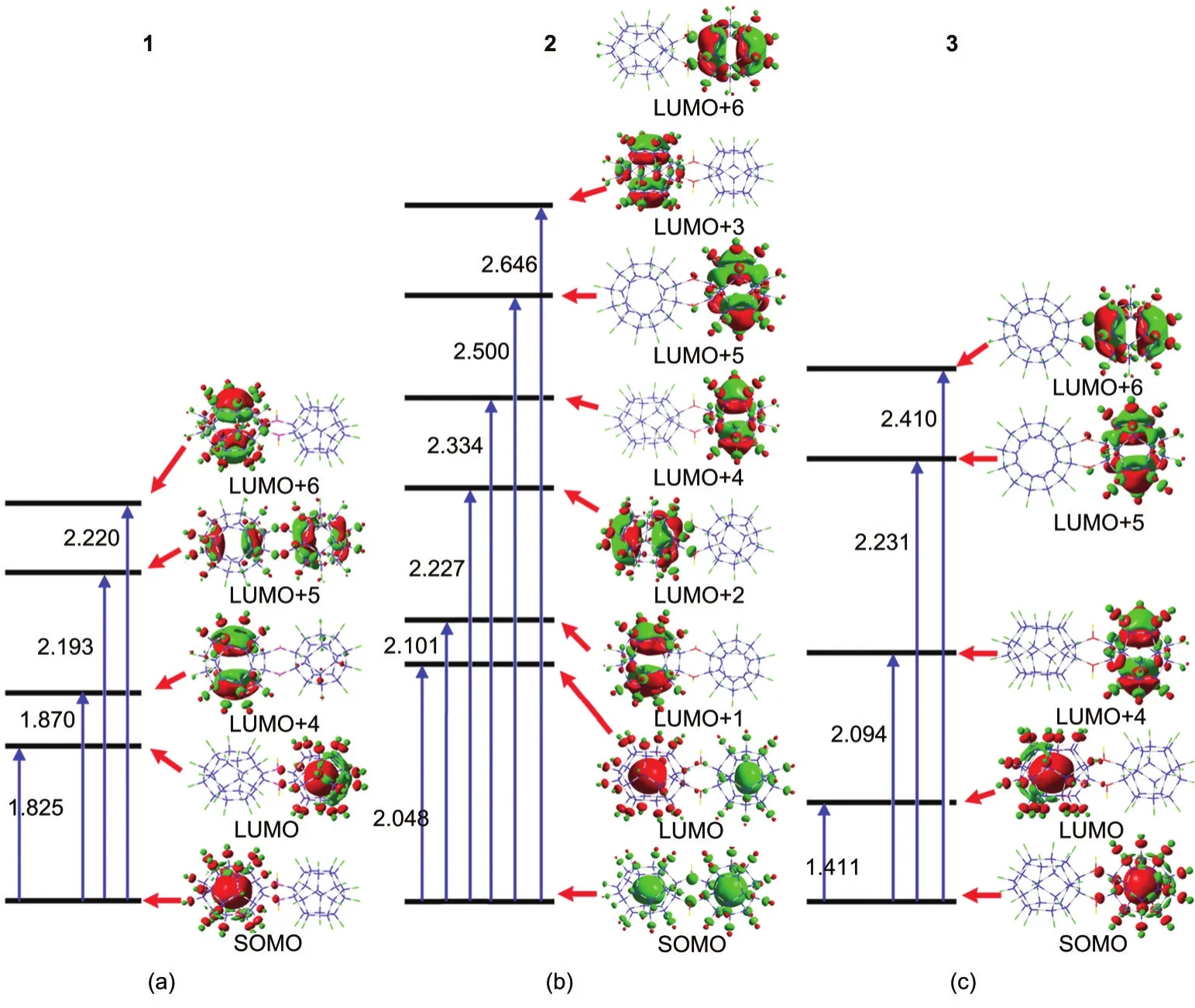
图3 1,2和3的额外电子激发能级图及相应的分子轨道Fig.3 Energy level Diagram of selected electronic excitations and the contour plots for their corresponding molecular orbitals(MOs)of 1(a),2(b),and 3(c)energy in eV

图4 外加电场诱导实现电子异构体间的相互转化Fig.4 Conversion among the electromersrealized by driving the external electric field

4 结论

基于密度泛函理论详细研究了非对称双笼型单分子溶剂化电子e-@C24F22(NH)2C20F18的电子异构体(1、2和3)及其非对称笼间额外电子迁移.主要结果归纳如下.

(1)电子异构体1、2和3属于一种非金属型的新型Robin-Day分子.对于1和3,额外电子分别定域在C24F22和C20F18笼里,对于2,额外电子则离域于两个非对称的笼中.

(2)在三个异构体中,1不管是在热力学上还是动力学上都是最稳定的,说明额外电子更喜欢占据在大笼子里;由于额外电子占据在对称性更高的小笼子里,3相对于1具有更大的偶极矩.

(3)对于1、2和3,从基态到第一激发态发生了笼间或笼内的额外电子迁移,并伴随着极大的偶极矩变化.

(4)在y轴方向上施加-0.0004和-0.0008 a.u.的临界电场,1的额外电子从C24F22笼部分和全部地迁移到C20F18笼中,即发生1→2→3笼间额外电子迁移;Ec为0.0004 a.u.时,3的额外电子从C20F18笼全部迁移到了C24F22笼中,即直接发生3→1笼间额外电子迁移.

Supporting Information Available: The Mulliken charges of different cages of 2,the IR spectra and optimized atom coordinates at B3LYP/6-31G(d)+4s4p level have been included. This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.

(1) Bally,T.Nat.Chem.2010,2,165.doi:10.1038/nchem.564

(2) Puschmann,H.F.;Harmer,J.;Stein,D.;Rüegger,H.;de Bruin, B.;Grützmacher,H.Angew.Chem.Int.Edit.2010,49,385. doi:10.1002/anie.200903201

(3) Gütlich,P.;Dei,A.Angew.Chem.Int.Edit.1997,36,2734. doi:10.1002/(ISSN)1521-3773

(4) Chaudhuri,P.;Hess,M.;Hildenbrand,K.;Bill,E.;Weyhermüller, T.;Wieghardt,K.Inorg.Chem.1999,38,2781.doi:10.1021/ ic990003g

(5) de Visser,S.P.;Ogliaro,F.;Harris,N.;Shaik,S.J.Am.Chem. Soc.2001,123,3037.doi:10.1021/ja003544+

(6) Chen,D.L.;Tian,W.Q.;Feng,J.K.;Sun,C.C.J.Chem.Phys. 2008,128,044318.

(7) Lu,X.;Chen,Z.;Thiel,W.;Schleyer,P.v.R.;Huang,R.; Zheng,L.J.Am.Chem.Soc.2004,126,14871.doi:10.1021/ ja046725a

(8)Wang,Y.Y.;Shi,Q.;Zhang,F.X.;Shi,Q.Z.Chin.J.Inorg. Chem.1999,15,557.[王尧宇,时 茜,张逢星,史启祯.无机化学学报,1999,15,557.]

(9) Robin,M.N.;Day,P.Adv.Inorg.Chem.Radiochem.1967,10, 247.

(10) Shriver,D.F.;Atkins,P.W.;Langford,C.H.Inorganic. Chemistry;Higher Education Press:Beijing,1997;pp 553-555; translated by Gao,Y.C.,Shi,Q.Z.,Li,P.R.[Shriver,D.F.; Atkins,P.W.;Langford,C.H.无机化学.高忆慈,史启祯,李丙瑞,译.北京:高等教育出版社,1997:553-555.]

(11) Demadis,K.D.;Hartshorn,C.M.;Meyer,T.J.Chem.Rev. 2001,101,2655.doi:10.1021/cr990413m

(12) Lambert,C.;Nöll,G.J.Am.Chem.Soc.1999,121,8434.doi: 10.1021/ja991264s

(13) Desfrançois,C.;Carles,S.;Schermann,J.P.Chem.Rev.2000, 100,3943.doi:10.1021/cr990061j

(14) Lee,H.M.;Lee,S.;Kim,K.S.J.Chem.Phys.2003,119,187. doi:10.1063/1.1576757

(15) Li,Y.;Li,Z.R.;Wu,D.;Li,R.Y.;Hao,X.Y.;Sun,C.C. J.Phys.Chem.B 2004,108,3145.doi:10.1021/jp036808y

(16)Matsuishi,S.;Toda,Y.;Miyakawa,M.;Hayashi,K.;Kamiya, T.;Hirano,M.;Tanaka,I.;Hosono,H.Science 2003,301,626. doi:10.1126/science.1083842

(17)Wang,Y.F.;Li,Z.R.;Wu,D.;Sun,C.C.;Gu,F.L.J.Comput. Chem.2010,31,195.doi:10.1002/jcc.v31:1

(18)Wang,Y.F.;Chen,W.;Yu,G.T.;Li,Z.R.;Wu,D.;Sun,C.C. J.Comput.Chem.2010,32,2012.

(19) Wang,Y.F.;Li,Z.R.;Wu,D.;Li,Y.;Sun,C.C.;Gu,F.L. J.Phys.Chem.A 2010,114,11782.doi:10.1021/jp1056557

(20) Wang,Y.F.;Li,Y.;Zhou,Z.J.;Li,Z.R.;Wu,D.;Huang,J.;Gu, F.L.ChemPhysChem 2012,13,756.doi:10.1002/cphc. 201100790

(21)Wang,X.;Ma,J.Phys.Chem.Chem.Phys.2011,13,16134.

(22) Zhou,Z.J.;Li,X.P.;Liu,Z.B.;Li,Z.R.;Huang,X.R.;Sun, C.C.J.Phys.Chem.A 2010,115,1418.

(23) Jordan,K.D.;Luken,W.J.Chem.Phys.1976,64,2760. doi:10.1063/1.432599

(24) Skurski,P.;Gutowski,M.;Simons,J.Int.J.Quantum Chem. 2000,80,1024.doi:10.1002/(ISSN)1097-461X

(25) Rienstra-Kiracofe,J.C.;Tschumper,G.S.;Schaefer,H.F.,III; Sreela,N.;Ellison,G.B.Chem.Rev.2002,102,231.doi: 10.1021/cr990044u

(26) Pathak,A.K.;Mukherjee,T.;Maity,D.K.J.Chem.Phys.2007, 127,044304.doi:10.1063/1.2756535

(27) Khan,A.Chem.Phys.Lett.2005,401,85.doi:10.1016/j.cplett. 2004.11.035

(28) Likura,H.;Tsuneda,T.;Yanai,T.;Hirao,K.J.Chem.Phys. 2001,115,3540.doi:10.1063/1.1383587

(29) Zhang,L.;Yan,S.;Cukier,R.I.;Bu,Y.J.Phys.Chem.B 2008, 112,3767.

(30) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 09, RevisionA.01;Gaussian Inc.:Wallingford,CT,2009.

(31) Aihara,J.J.Phys.Chem.A 1999,103,7487.doi:10.1021/ jp990092i

(32) Simons,J.J.Phys.Chem.A 2008,112,6401.doi:10.1021/ jp711490b

June 8,2012;Revised:July 30,2012;Published on Web:July 30,2012.

Asymmetrical Inter-Cage Electron Transfer Electromers and Their Transfer Characteristics under Electric Fields

WANG Yin-Feng1,*HUANG Jian-Gen1ZHOU Guang-Pei1LI Zhi-Ru2,*
(1Jiangxi Province Key Laboratory of Coordination Chemistry,Institute of Applied Chemistry,School of Chemistry and Chemical Engineering,Jinggangshan University,Jiʹan 343009,Jiangxi Province,P.R.China;2State Key Laboratory of Theoretical and Computational Chemistry,Institute of Theoretical Chemistry,Jilin University,Changchun 130023,P.R.China)

The asymmetrical,double-cage-shaped,single molecular solvated electron compounds e-@C24F22(NH)2C20F18(1,2,and 3)were investigated based on density functional theory(DFT).This work revealed a novel species of electromer consisting of asymmetrical inter-cage electron-transfer isomers. These inter-cage electron-transfer isomers belong to a new form of Robin-Day class II-III molecules.1 and 3 are Robin-Day class II,with the excess electron inside the C24F22and C20F18cages respectively,while 2 is class III with the excess electron inside both cages.These electromers were found to exhibit significantly different dipole moments.The application of external electric fields of-0.0004 or-0.0008 a.u.in the y-axis direction of 1 resulted in either partial or whole transfer of the excess electron from C24F22to C20F18,allowing conversion from 1 to 2 or 3.An Ecvalue of 0.0004 a.u.was determined,indicating that the excess electron can wholly transfer fromthe C20F18cage toC24F22,resulting in conversion from 3 to1 without going through 2.

Electric field inducement;Robin-Day molecule;Single molecular solvated electron; Electromer;Asymmetrical inter-cage electron transfer

10.3866/PKU.WHXB201207302

∗Corresponding authors.WANG Yin-Feng,Email:cyclont@yeah.net;Tel:+86-796-8100490.LI Zhi-Ru,Email:lzr@jlu.edu.cn; Tel:+86-431-8498964.

The project was supported by the Science and Technology Project of Jiangxi Provincial Department of Science&Technology,China (20114BAB213007),Science and Technology Project of Jiangxi Provincial Department of Education,China(GJJ12486),National Natural Science Foundation of China(21173098),DrStart-up Fund Research of Jinggangshan University,China(JZ10045),and Foundation of State Key Laboratory of Theoretical and Computational Chemistry of Jilin University,China.

江西省科技厅自然科学基金(20114BAB213007),江西省教育厅自然科学基金(GJJ12486),国家自然科学基金(21173098),井冈山大学博士启动基金(JZ10045)及吉林大学理论计算化学国家重点实验室开放课题基金资助项目

O641