大学本科非数学专业《线性代数》课程教学中的思维训练

2012-12-08蔡美香

湖南科技学院学报 2012年8期

关键词：线性方程组行列式线性代数

蔡美香

(中南林业科技大学理学院，湖南长沙 410004)

大学本科非数学专业《线性代数》课程教学中的思维训练

蔡美香

(中南林业科技大学理学院，湖南长沙 410004)

在大学本科非数学专业《线性代数》课程教学中的思维能力的训练主要是逻辑思维能力与创造性思维能力的训练。论文对逻辑思维的分析与综合、分类与比较、抽象与概括，归纳与演绎四种思维过程，创造性思维中的发散性思维和逆向思维分别举例说明其训练过程，以期达到提高学生整体思维水平的目的。

《线性代数》；逻辑思维能力训练；创造性思维能力训练。

1 引言

美国自然科学基金会最近指出：“当代自然科学的研究正在日益呈现出数学化的趋势”。数学在当代科技、文化、社会、经济和国防等诸多领域有着特殊重要的地位。《线性代数》作为高校理工科专业甚至部分文科专业开设的一门数学公共基础课，着重训练学生掌握一些有用的运算工具和算法，为学生学习本专业的其他课程提供有力的数学基础，并为学生处理实际应用问题提供解决多元线性问题的有效工具。同时，《线性代数》课程注重对学生进行逻辑思维能力和创造性思维能力的训练，这两种思维能力的培养，将会使学生受益终生。

作为《线性代数》的授课教师，在教学上要注意处理好讲授算法和进行思维训练这两方面的关系，合理的安排教学时间。在长期的教学实践中发现，大学本科非数学专业的学生对算法的掌握度普遍较好，而对思维训练普遍反映较难，部分同学甚至有抵触情绪。鉴于此，探讨在《线性代数》的教学过程中这两种思维能力的训练方法是非常有必要的。

2 《线性代数》课程教学中逻辑思维能力的训练

逻辑思维，是指人们在认识过程中借助于概念、判断、推理等思维形式能动地反映客观现实的理性认识过程，又称理论思维。只有经过逻辑思维，人们才能达到对具体对象本质的把握，进而认识客观世界。它是人的认识的高级阶段，即理性认识阶段。逻辑思维能力是指正确、合理思考的能力，即对事物进行观察、比较、分析、综合、抽象、概括、判断、推理的能力，采用科学的逻辑方法，准确而有条理地表达自己思维过程的能力。

逻辑思维能力不仅是学好数学必须具备的能力，也是学好其他学科，处理日常生活问题所必须的能力。逻辑思维能力是在发现问题与解决问题的过程中锻炼出来的。在《线性代数》的教学过程中，最有效的训练学生逻辑思维能力的方法是教师提问，由学生独立思考或相互讨论得出答案。具体来说，由于逻辑思维有分析与综合、分类与比较、抽象与概括，归纳与演绎四种思维过程，下面分别就《线性代数》的教学过程举例说明。

2.1 分析与综合

分析是在思维中把对象分解为各个部分或因素，分别加以考察的逻辑方法。综合是在思维中把对象的各个部分或因素结合成为一个统一体加以考察的逻辑方法。

以行列式按行展开法则的证明为例。考虑的对象为一般的n阶行列式应用分析法，将之分解为如下n个特殊的行列式：

分别考虑每一个特殊行列式的值，通过逐行对调与逐列对调，可将第i行的元素aij调到第一行第一列的位置，且除第i行外，其余行的元素的上下左右位置不变，可分别得出如上n个行列式的值分别为提出问题：综合考虑这n个行列式的和，会有什么结论？这就是行列式按第i行展开公式

2.2 分类与比较

根据事物的共同性与差异性就可以把事物分类，具有相同属性的事物归入一类，具有不同属性的事物归入不同的类。比较就是比较两个或两类事物的共同点和差异点，通过比较就能更好地认识事物的本质。

以逆矩阵概念的提出为例。众所周知，数有加、减、乘，除四种基本运算，矩阵也有加、减、乘积运算，唯独没有“除”的运算。对于数的除法，有，若b=0，那么a÷b无意义。提出问题：矩阵运算中是否有类似于“倒数”的概念呢？在数字运算中，有一个特殊的数字“1”，当a≠0时，有联想到矩阵当中有一个特殊矩阵E，它在矩阵中的特殊性类似于数字“1”在数中的特殊性，于是顺理成章的提出逆矩阵的概念，若有则记或继续思考矩阵A存在逆矩阵的充要条件，必要性直接由定义等式两边同时做行列式运算可推出充分性需另证（由可得）。当矩阵可逆时，若形式上需要除以一个矩阵，可以用乘上这个矩阵的逆矩阵来做，比如解系数矩阵为方阵的线性方程组当|A|≠ 0时，但是这里不得不比较矩阵乘以逆矩阵与数乘以倒数的差别但前例这是因为数与数相乘是可以交换顺序的，而矩阵与矩阵相乘，不一定能交换顺序。矩阵形式上的除法本质上是做矩阵乘法，如上例本质上是由等式两边同时左乘得来，这里一定要注意是左乘逆矩阵还是右乘逆矩阵。

2.3 抽象与概括

抽象就是运用思维的力量，从对象中抽取它本质的属性，抛开其他非本质的东西。概括是在思维中从单独对象的属性推广到这一类事物的全体的思维方法。

以用矩阵的初等变换解线性方程组为例，取教材[1]中第三章第一节中引例：

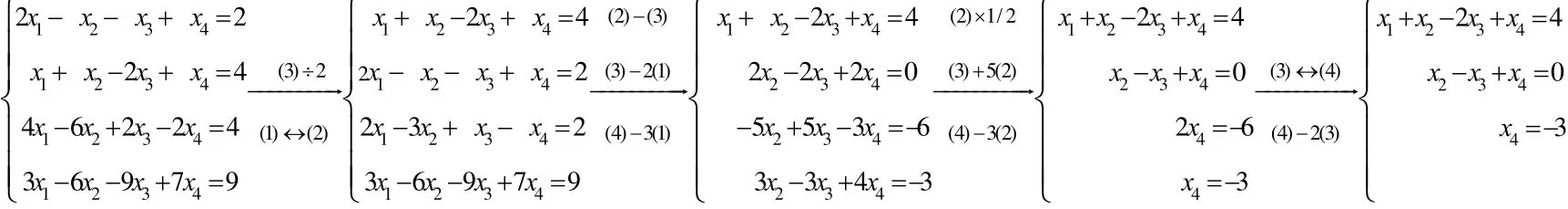
在用消元法解线性方程组的过程中对线性方程组施行了如下三种变换：①交换两个方程的位置；②某个方程乘上一个不为零的数；③一个方程乘上一个数后加到另一个方程。施行这三种变换后得到的新的线性方程组与原方程组是同解的。我们对如上过程进行抽象分析，就会发现，消元的本质就是通过如上三种变换将某个方程的某个未知变元的系数变为0。若固定未知变元的顺序，第1-4列分别代表第五列代表常数项b，实际上以上过程只是对方程组的系数和常数进行运算，未知数并没有参与运算。于是，可将方程组的系数和常数构成一个增广矩阵，对增广矩阵施行如下相应的初等行变换：

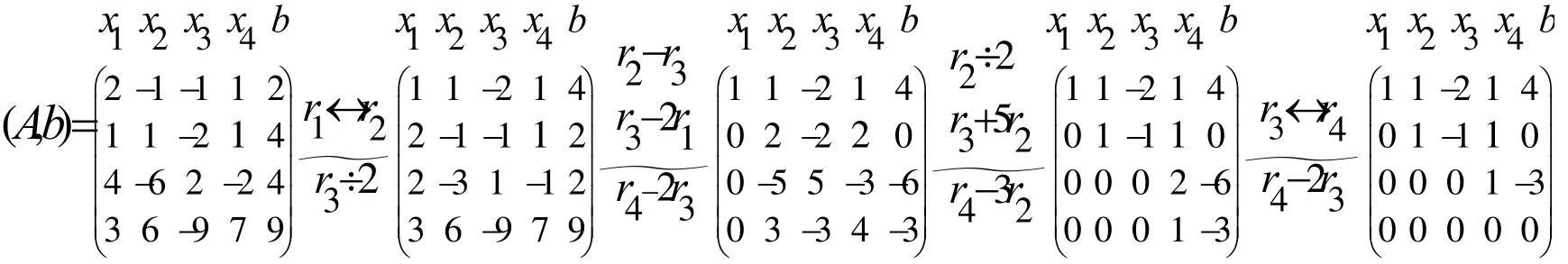
继续施行行初等变换直到将矩阵化成行最简形，得出方程组的通解。对如上过程进行概括总结，可以将矩阵的初等行变换应用到解一般的具有n个未知变元，m个方程的线性方程组中。同时，提出问题：“是否可以应用矩阵的初等列变换来解题呢？”只要学生对这种方法的本质把握好了，相信不难得出“前n-1列可以交换，但要注意各列所代表的未知变元要跟着走，最后一列代表常数列，不可以和前面的列进行交换”的正确答案。这里还可继续对学生进行创造性思维的训练：提出问题：矩阵的初等列变换对不同形式的通解起了一个什么样的作用？学生会继续思考：行阶梯形矩阵中阶梯口所在的列所代表的未知变元为非自由未知量，应用矩阵的初等行变换解线性方程组，有尽量选择前面的未知变元做非自由未知量的趋势，而矩阵的初等列变换可能会改变非自由未知量的选择，因此可能会得到不同形式的通解。

2.4 归纳与演绎

归纳是从个别性的前提推出一般性的结论，前提与结论之间的联系是或然性的。以非齐次线性方程组Ax=b解的结构为例。提出问题：能否由齐次线性方程组Ax=0的通解归纳得出Ax=b的通解？若Ax=0的通解为设Ax=b的任意的一个解为的一个特解，那么必为的解，可以得到于是得出非齐次线性方程组Ax=b解的结构：非齐通=齐通+非齐特。

演绎是从一般性的前提推出个别性的结论，前提与结论之间的联系是必然性的。以矩阵的对角化与对称矩阵的对角化为例。我们知道，n阶矩阵A能够对角化的充要条件是存在n个线性无关的特征向量构成可逆矩阵使得这是对任意矩阵的一个一般性的结论。提出问题：对称矩阵对角化时有什么更特殊的结论吗？由于对称矩阵的特征值全为实数，且不同的特征值所对应的特征向量是正交的，可以得出一个更特别的结论：对称矩阵一定可以对角化，且存在矩阵P，不但是可逆的，而且是正交的，使得

3 《线性代数》课程教学中创造性思维能力的训练

创造性思维是一种具有开创意义的思维活动，即开拓人类认识新领域，开创人类认识新成果的思维活动。狭义上，它往往表现为发明新技术、形成新观念，提出新方案和决策，创建新理论。从广义上讲，创造性思维不仅表现为作出了完整的新发现和新发明的思维过程，而且还表现为在思考的方法和技巧上，在某些局部的结论和见解上具有新奇独到之处的思维活动。

在《线性代数》课程的教学过程中主要是尝试训练学生广义上的创造性思维。学生形成创造性思维的主要条件是强烈的好奇心、坚强的信念和永不满足的求知欲，以及有关的广博知识，主要表现在想像、尤其是创造性想像的参与。对于非数学专业的学生，除了要关注一般人才的培养，还需重视各类优秀人才的培养问题。对学生创造性思维的训练，为优秀人才的迅速成长创造了良好的条件，营造了良好的环境。在《线性代数》课程的教学实践中，对学生创造性思维的训练，主要表现在对学生发散性思维和逆向思维的引导上。

3.1 发散性思维

发散性思维由美国著名心理学家Guiford于1967年提出，创造性思维的本质是发散思维，又称求异思维、扩散思维等，是指沿着各种不同的方向去思考，重组眼前的信息和记忆系统的信息，从而产生出大量独特的新思想。它克服了常规思维中单向思维的缺陷，是一种不依常规、寻求变异，从多方面探索答案的思维形式，是创造性思维的重要组成部分。

“一题多解”是发散性思维的一种典型表现，体现在课程内容上，即“一个内容，多种解释”。以最简单的解线性方程组为例，继续将前述引例进行初等行变换，直至化成行最简形，可得与原方程组同解的线性方程组为