应用型本科《线性代数》与matlab教学改革
2012-12-08刘忠志
刘忠志
(广东白云学院 基础教学部,广东 广州 510450)
应用型本科《线性代数》与matlab教学改革
刘忠志
(广东白云学院 基础教学部,广东 广州 510450)
本文根据应用型本科的特点和《线性代数》教学实践,运用数学软件“matlab”解决《线性代数》中的计算问题,实行笔算与电脑算相结合的教学改革与探讨,取得较好的教学效果,深受学生欢迎。
应用型本科;线性代数教学;“matlab”计算;教学改革
Matlab是数学计算软件,功能非常强大,随着科学技术的不断发展,笔算与电脑算相结合是未来发展的必然趋势,光用笔算不行,光用电脑算也不行,为什么呢?因为有些数学模型,用笔算很难算出,有的几乎不可能。但用电脑算(数学软件)很容易算出结果,来得快。但不能全依赖于电脑,基本计算方法、必要的简单的笔算能力是要掌握的,有些简单的问题用笔算还快一点,再则电脑算有它的局限性,它是死算,是机器算,不是人算,过份使用它会失去数学的一个重要作用:即逻辑思维能力的培养。例如:现在经商的、或上街买菜算数都用计算器,很少用笔算,难道叫小学生不要学笔算加、减、乘、除了吗?,专学用计算器来算,那就麻烦了,将成为机器的奴隶,影响智力的开发。所以只有笔算和电脑算“两算”相结合、互相弥补才是最佳途径。
学过线性代数的人都知道,线性代数的特点是计算量大,单独用笔算是很麻烦的,特别在实际应用中,更为突出,例如:
案例:某食品厂收到某种食品订单,要求这种食品由甲、乙、丙、丁四种原料做成,且该食品中含蛋白质、脂肪和碳水化合物的比例分别为15%、5%和12%,而甲、乙、丙、丁四种原料中含蛋白质、脂肪和碳水化合物的百分比由下表给出,这四种原料各用多少才配置出满足要求的食品?

?
解:设甲、乙、丙、丁占食品的百分比分别为x1、x2、x3、x4
上面方程若用笔算来解,比较麻烦,但用matlab 解只用两分钟(电脑输入过程)就可以解出
具体过程如下:
>>A=[1 1 1 1 1;20 16 10 15 15;3 8 2 5 5;10 25 20 5 12]
>>rref(A) 回车得:
ans = 1.0000 0 0 0 0.1031
0 1.0000 0 0 0.2147
0 0 1.0000 0 0.1460
0 0 0 1.0000 0.5362
注:A是增广矩阵,rref(A)是计算命令,ans是计算结果:第一、二、三、四列分别表示x1、x2、x3、x4的位置,最后一列分别是x1、x2、x3、x4的得数。
用matlab解决数学问题是死算,只知其算,不知其理,所以笔算方法要给学生讲清楚。
线性代数中的计算主要有:行列式的计算、矩阵的运算、解线性方程组、求特征值特征向量、矩阵的正交化,化标准二次型等等,每一个问题都是比较复杂的计算,用笔算是很繁琐的,我们的教学方法模式如下:
案例→基本知识传授→使用数学软件matlab→应用(祥见文[1])
1、行列式的计算:先引进实用案例,然后介绍行列式的基本知识(定义、性质等),再讲解二阶、三阶、简单四阶行列式的笔算方法,对于一般四阶或四阶以上行列式的计算用电脑matlab软件来计算,但是对于一般的n阶行列式用电脑不一定能算出结果,应采用笔算方法,因为n阶行列式计算可以训练大脑思维能力,培养发现规律的能力。

解法二(电脑算):
>>A=[2 -5 1 2;-3 7 -1 4;5 -9 2 7;4 -6 1 2];
>>det(A) 回车得:
ans = -9
提问学生:哪种方法好?百分之百的学生赞同电脑算好,但笔算的道理还是要给学生讲清楚。
2、矩阵的运算:教学方法同上,特别指出的是,矩阵的乘法、矩阵的乘方和求逆矩阵主要以电脑计算为主,三阶或三阶以下矩阵的乘法、乘方(乘方三次以下)运算用笔算,
案例:某城市的总人口是固定的,开始时有30%的居民住在市区,70%的住在郊区.由于搬迁变化,每年有6%的市区居民搬到郊区去住,而有2%的郊区居民搬到市区来住.问10年后市区和郊区的居民人口的比例是多少? 30年、50年、60年呢?
>>A=[0.94 0.02;0.06 0.98];
>> x0=[0.3 0.7]'; x10=A^10*x0, x50=A^50*x0,x60=A^60*x0 回车得:
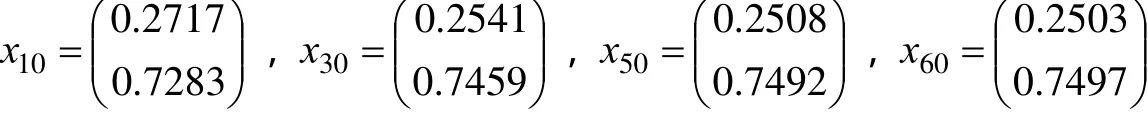
所以10年后市区和郊区的居民人口的比例是0.2717:0.7283;
30年后市区和郊区的居民人口的比例是0.2541:0.7459;
50年后市区和郊区的居民人口的比例是0.2508:0.7492。
60年后市区和郊区的居民人口的比例是0.2503:0.7497。
案例教学主要突出应用。
3、逆矩阵的教学方法:首先介绍逆矩阵的定义、性质、笔算求逆矩阵方法:

以及给学生讲清楚为什么这样求逆矩阵的道理之后,举例如下:
解法一(笔算):
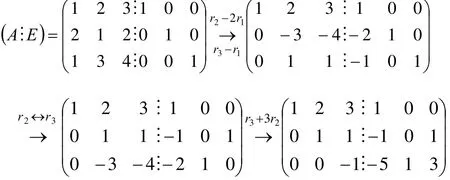
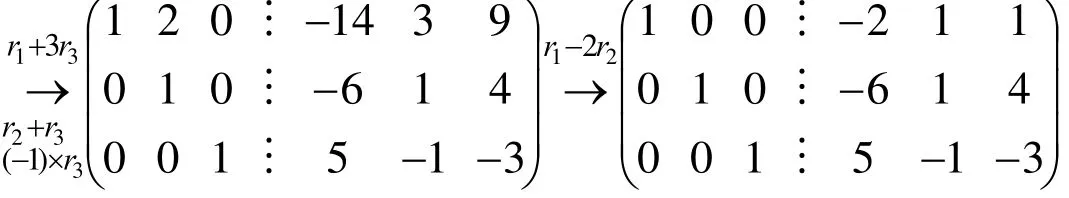
解法二(电脑算):
>> A=[1 2 3;2 1 2;1 3 4];
>> A^(-1) 回车得:
ans = -2.0000 1.0000 1.0000
-6.0000 1.0000 4.0000
5.0000 -1.0000 -3.0000
提问学生:哪种方法好?百分之百的学生赞同电脑算好。
这样使学生既懂得了用笔算求逆矩阵方法,也懂得了用电脑求逆矩阵的方法,供学生选择最佳方法。
4、解线性方程组(以解齐次线性方程组为例,非齐方程组前面已有例):

(x3,x4为自由未知量)
解法二:(电脑算)
>>A=[1 -1 5 -1;1 1 -2 3;3 -1 8 1;1 3 -9 7];
>> D=null(A,’r’) 回车得:齐通的有理解基
D =-1.5000 -1.0000
3.5000 -2.0000
1.0000 0
0 1.0000
注:若不加’r’,用D=null(A),得出两个“单位正交向量”非有理数.
5、求特征值、特征向量:
若用笔算求特征值、特征向量是相当麻烦的一件事,笔算方法及其原理一定告诉学生,但在实际应用中一般用电脑算。在下例中,只介绍用电脑求解:
解法一(笔算):略。
解法二(电脑算)
>>A=[0 1 1;1 0 1;1 1 0]; >> [P,D]=eig(A) (P:特征列向量,D:对角阵特证值),
回车得:
P =-0.7152 0.3938 0.5774
0.0166 -0.8163 0.5774
0.6987 0.4225 0.5774
(特征向量为小数,主要是单位正交化了。正交矩阵定义:P'*P = E )
我们知道用施密特方法把向量组正交化是相当麻烦的,而电脑给出的结果直接是正交化了的向量组,真是太好了,这在实际应用中有很大帮助。
线性代数中还有很多复杂的计算问题,用以上方法教学,会收到事半功倍的效果,深受学生欢迎,这里就不再一一举例了。这样教学还可以节约较多的课时,用于讲解难点内容(如线性相关、线性变换、向量空间等内容)。
微积分教学特别是一元微积分教学应等到期末再讲matlab计算,否则,学生倾向matlab电脑计算,影响笔算能力的培养。作为现代大学生掌握运用matlab数学软件计算很有必要,但必要的笔算能力是要具备的。
[1]刘忠志.应用型本科高等数学教学与“CDIO”教学改革初探[J].湖南科技学院学报,2011,(4).
O13
A
1673-2219(2012)08-0007-06
2012-04-21
第二批院级教学成果培育项目“应用型本科《高等数学》教学改革研究与实践”。
刘忠志(1959-),男,湖南永州人,广东白云学院基础教学部副教授,研究方向为高等数学教育研究。
(责任编校:何俊华)

