压缩真空中理想玻色-爱因斯坦凝聚体杂质间的相互作用
2012-12-04姜文英潘淑梅郑泰玉
王 艳, 杨 慧, 郑 丽, 姜文英, 潘淑梅, 郑泰玉
(1. 长春职业技术学院 汽车分院, 长春 130033; 2. 东北师范大学 物理学院, 长春 130024; 3. 大连工业大学 信息科学与工程学院, 辽宁 大连 116034; 4. 桂林电子科技大学 电子工程与自动化学院, 广西 桂林 541004)
玻色-爱因斯坦凝聚(BEC)在光学、 原子分子物理、 凝聚态物理、 激光物理、 统计物理和材料学等领域应用广泛[1-4]. Casimir效应在量子场论、 凝聚态物理、 原子和分子物理、 万有引力和宇宙学及数学物理等领域应用广泛[5-6]. Casimir力是由真空电磁场中的零点涨落产生的, 并在实验上分别测量到吸引力和排斥力[7-8]. 目前, Casimir效应的研究已引起人们广泛关注[9].
在凝聚体中, 若将杂质作为边界, 则系统的能量与杂质间的距离有关, 杂质间也会产生作用, 这种类似于真空中的Casimir效应称为类Casimir效应[10]. 本文应用Riemann Zeta函数研究一维真空压缩态玻色-爱因斯坦凝聚体杂质间的Casimir效应.
1 杂质间的Casimir力
本文采用类似文献[10]的模型, 假设Bose-Einstein凝聚体系采用一维有质量的标量场方程描述:
(1)
其中m为玻色子质量. 其边界条件满足
φ(t,0)=φ(t,a).
(2)
将式(2)代入式(1)可得:
(3)
其中
(4)
对场量子化可得
(5)
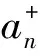
(6)
能量密度算符为
(7)
系统的Hamilton量为

(8)
将式(7)代入式(8)可得系统的Hamilton量为
(9)
在压缩真空态下, 杂质间的能量可表示为
(10)
其中Sn为单模压缩算符, 表达式为
(11)
式中λn为第n个模式的压缩系数.
利用
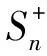
(12)
以及式(3)~(9), 可将式(10)变为
(13)
为简单, 考虑λn=λ,m=0的情况. 利用公式
(14)
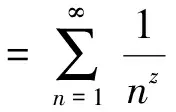
(15)
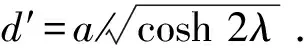
当λ=0时, 可得真空态下的Casimir力
(16)
由方程(15)和(16)可见, 在压缩态下相距为d′的杂质间Casimir力与真空态下相距为a的杂质间Casimir力相等.
2 数值计算与分析
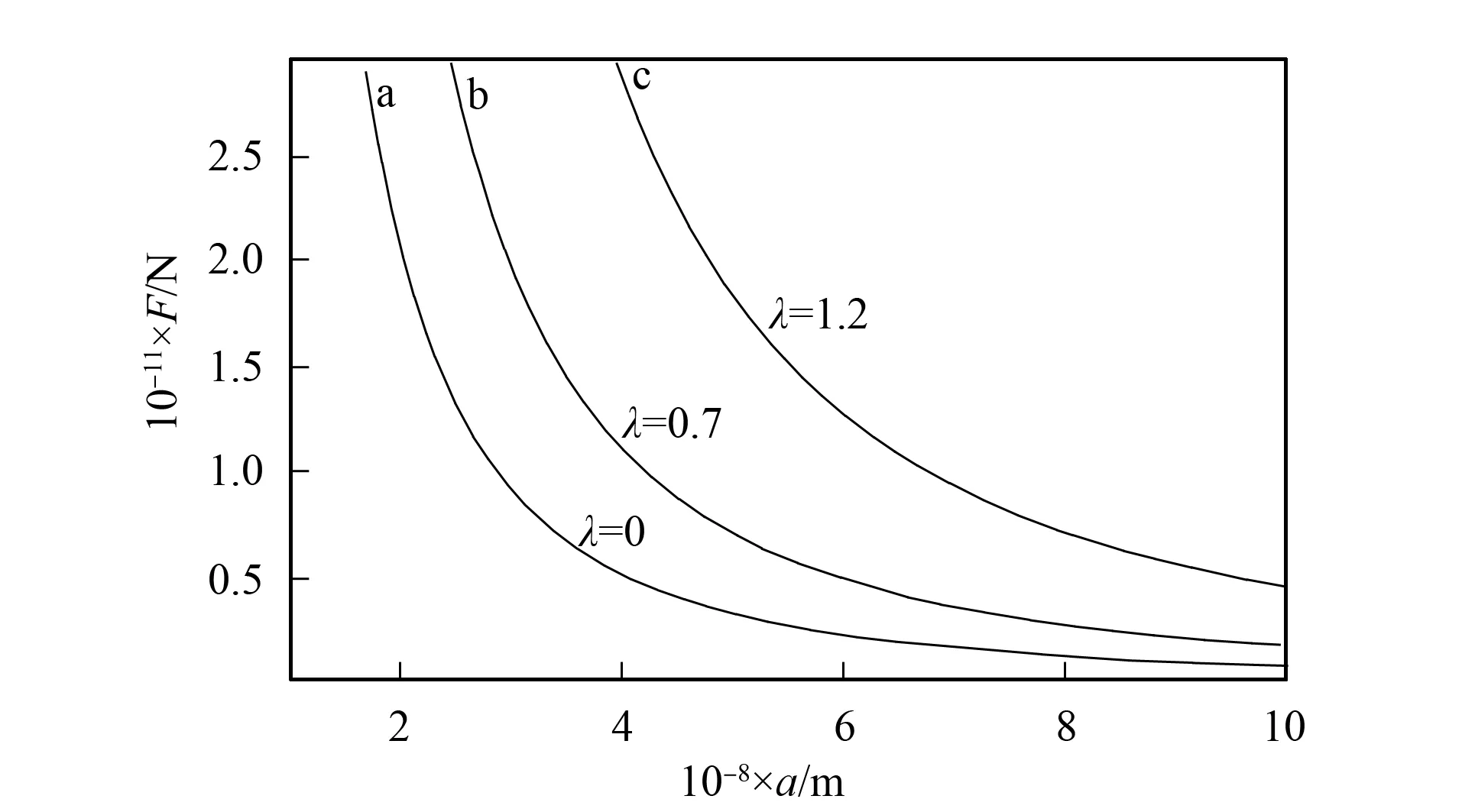
图1 压缩态的类Casimir力F随杂质间 距离a的变化关系Fig.1 Plots of the force F versus a at different values of λ
在不同的压缩系数λ下, 压缩态的类Casimir力F随杂质间距离a的变化关系如图1所示, 其中曲线a对应λ=0, 即真空态的情况; 曲线b和c分别对应λ=0.7和λ=1.2, 即压缩态情况. 由图1可见: Casimir力F随杂质间的距离a增大而变小; 压缩系数越大, 力越大; 在真空态下力最小.
综上, 本文计算了压缩态下理想玻色-爱因斯坦凝聚体中的类Casimir能量和力, 并给出了类Casimir力随压缩系数和杂质间距离的变化关系. 对于一维情况, 在压缩态或真空态下, Casimir能量与距离均为负二次幂的关系. 由于d′>a, 因此当玻色-爱因斯坦凝聚体中杂质的间距相同时, 压缩态下的杂质间类Casimir力大于真空态下的杂质间类Casimir力. 表明在压缩态下更利于在实验中测得玻色-爱因斯坦凝聚体中杂质间的力.
[1] Anderson M H, Ensher J R, Mathews M R, et al. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor [J]. Science, 1995, 269: 198-201.
[2] Bradley C C, Sackett C A, Tollett J J, et al. Evidence of Bose-Einstein Condensation in an Atomic Gas with Attractive Interactions [J]. Phys Rev Lett, 1995, 75(9): 1687-1690.
[3] Davis K B, Mewes M O, Andrews M R, et al. Bose-Einstein Condensation in a Gas of Sodium Atoms [J]. Phys Rev Lett, 1995, 75(22): 3969-3973.
[4] WANG Yan, LI Tong, ZHENG Li, et al. The Interaction between Contaminants in Ideal Bose-Einstein Condensates for Periodic Boundary Condition [J]. Journal of Northeast Normal University: Natural Science Edition, 2011, 43(4): 81-83. (王艳, 李彤, 郑丽, 等. 周期边界下波色爱因斯坦凝聚体杂质间相互作用 [J]. 东北师大学报: 自然科学版, 2011, 43(4): 81-83.)
[5] Casimir H B G. The Energy between Two Large Uncharged Conducting Plates [J]. Proc Kon Nederl Akad Wet, 1948, 51: 793-797.
[6] Klimchitskaya G L, Mohideen U, Mostepanenko V M. Theoretical Ingredients of a Casimir Analog Computer [J]. Rev Mod Phys, 2009, 81: 1827-1885.
[7] Lamoreaux S K. Demonstration of the Casimir Force in the 0.6 to 6 mm Range [J]. Phys Rev Lett, 1997, 78(1): 5-8.
[8] Munday J N, Capasso F, Parsegian V A. Measured Long-Range Repulsive Casimir-Lifshitz Forces [J]. Nature, 2009, 457: 170-173.
[9] Sushkov A O, Kim W J, Dalvit D A R, et al. Observation of the Thermal Casimir Force [J]. Nature Physics, 2011, 7: 230-233.
[10] Alexander Oshmyansky. A Proposed Casimir-Like Effect between Contaminants in Ideal Bose-Einstein Condensates [J/OL]. 2007-03-08. http://arXiv:cond-mat/0703211v1.
