Cochran－Armitage趋势检验不同赋值的模拟研究

南方医科大学公共卫生与热带医学学院生物统计系(510515) 何春拉 潘建红 陈 靖 陈平雁

Cochran－Armitage趋势检验是一种用于分析1个二分类变量和1个有序分类变量关联性的统计方法，由 Cochran和 Armitage创建和完善〔1－2〕。趋势检验中等级变量的赋值分为两类，即等距赋值和非等距赋值，前者只有一种情况，后者则包括平均秩次(以下简称均秩)赋值，极大极小效率稳健检验(maximin efficiency robust test，MERT)赋值〔3－4〕，基于生存分析的 poly－3和 poly－k 赋值方法〔5－6〕，以及根据分布或其他准则确定的赋值方法。然而，由于等级变量赋值没有统一标准而使得趋势检验方法在应用中颇受争议。Kendall、Staurt和Gross等质疑趋势检验方法的科学性，并倡导采用秩和检验处理有序分类数据〔7－9〕。Graubard和Korn则建议:(1)当赋值和有序分组的实际分布情况一致时，趋势检验的结果和意义最大;(2)在缺乏有序分组数据的分布信息情况下，等距赋值是最佳选择;(3)尽量避免采用均秩赋值〔10〕。鉴于上述情况，我们拟通过Monte Carlo模拟研究，比较等距、均秩以及基于等距与均秩赋值的MERT等三种赋值方法对趋势检验结果的影响，以期为应用Cochran－Armitage趋势检验时如何赋值提供依据。

方 法

1.赋值方法

Cochran－Armitage趋势检验在计算上可分为校正和非校正两种，在思想上分为正态近似和确切概率两种。本研究以非校正正态近似Cochran－Armitage趋势检验为代表，检验统计量的计算公式如下:

式中，N为两组样本量的合计;R为病例组样本量;ri为病例组第i个等级的例数;ni为第i个等级两组合计例数;xi为第i个等级的赋值，不同的赋值方法得到的检验结果显然不同，这正是下面要深入探讨的。

等距赋值方法 是指相邻两个等级赋值的差为一个不等于0的常数，即按照等级顺序的赋值是个等差序列，表达为:xi－ xi－1=xi－1－ xi－2= … =x2－ x1=a(a是不等于0的常数)。

均秩赋值方法 即按照每个等级的平均秩次进行赋值，令xi为第i个等级的赋值，则

MERT方法 在统计学应用中，有些数据的精确分布模型往往是未知的。在这种情况下，如果单纯以检验效能为评判标准，从一族(ξ:{fi:i:=1，…，I})候选模型中选取一个检验效能最大但却不符合数据具体分布模型的检验统计量，那么这时会因忽略数据的具体分布形态而造成统计效率的损失。MERT方法可减少这种效率损失。MERT方法是一种稳健的统计学方法，它基于极大极小效率的原理，先计算候选统计模型中各个模型检验统计量Zi相对于其他模型检验统计量Zj的渐进相对效率)，然后从中选择渐进相对效率值最小的一对检验统计量Z，Zi＞ =ρ12)计算 MERT 统计量。如果 ρ12大于零且满足 MERT 条件(ρ1i+ ρ2i≥1+ ρ12(i∈I))，则 MERT统计量等于［2(1+ρ12)］1/2(Z1+Z2)，而 MERT的极大极小效率为(1+ρ12)/2。如果ρ12不满足MERT条件，则计算上述得到的MERT统计量Z12与候选模型各个检验统计量的渐进相对效率，并找出渐进相对效率值最小的检验统计量 Z3，若满足MERT条件，则MERT统计量为三个检验统计量的线性组合若不满足MERT条件，重复此步骤直至MERT条件满足为止。

以上是针对I≥3的情况，当数据只有I=2种候选统计模型时，MERT统计量计算相对简单。此时只需先计算出两个检验统计量的相对渐进效率ρ212，再计算 MERT 统计量等于［2(1+ ρ12)］－1/2(Z1+Z2)〔3，4〕。

2.评价方法

比较三种方法的I类错误率和检验效能。

3.模拟方法

本研究用统计软件 SAS9.2编程，采用 Monte Carlo方法模拟，用SAS9.2中的RANTBL过程产生离散随机函数，即2×k有序分类数据，每种参数组合重复10000次〔11〕。参数设置上考虑两个参数，即每个等级的样本量(ni)和阳性率(pi)，两个参数的组合分别见I类错误率比较的参数设置(表1)和检验效能比较的参数设置(表2)。

表1 I类错误率比较的参数设置

结 果

当各有序分组的样本量相同时，即当n1=n2=…=ni时，等距﹑均秩和基于等距和均秩的MERT三种赋值方法趋势检验的结果相同。

当各有序分组的样本量不完全相等时，不同参数组合的I类错误率以等距赋值最低，均秩赋值次之，MERT法最高(见图1)。三种赋值方法的检验效能非常接近，(见图2)，当每个等级的阳性率较大时(P＞0.10)，三种赋值方法的检验效能几乎相等;当有一个等级的阳性率较小时(Pi=0.05)，如组合代码为1，4，7，12，32 的参数组合(见表2)，等距赋值的检验效能略低于均秩赋值和MERT法，此时的检验效能普遍偏低。

图1 三种赋值方法I类错误率的比较

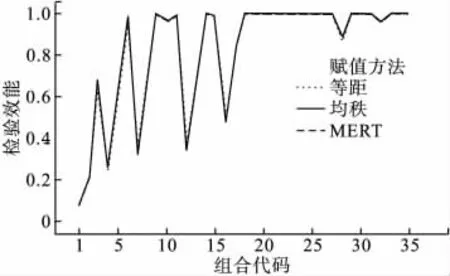
图2 三种赋值方法检验效能的比较

讨 论

Cochran－Armitage趋势检验因赋值方法不同导致结果有异。Armitage，Chakraborti和Schaafsma等提倡采用等距赋值方法〔2，12〕。Graubard 和 Korn 认为，当赋值的分布与有序数据分布一致时趋势检验结果的效能最高〔10〕。Neuhäuser也发现了这个规律〔13〕。但是，获取有序资料的真实分布在现实中往往难以实现。此外，这种赋值方法也有其缺陷，一方面它的复杂过程可能给非统计专业研究人员的应用带来困难;另一方面它的开放性的特点可能导致滥用赋值以达到预期目的的情况出现。

本研究对Cochran－Armitage趋势检验中三种赋值方法，即等距赋值﹑均秩赋值和基于等距及均秩的MERT法赋值方法，通过计算机模拟进行了比较，发现三种方法的检验效能非常接近，但I类错误率以等距赋值方法最低。在统计学中，当几种方法的检验效能相当的情况下，I类错误率越小越好。因此，根据本研究模拟结果及应用的便利性，我们认为有序分类数据的Cochran－Armitage趋势检验采用等距赋值更值得提倡。

1.Cochran WG.Some methods for strengthening the common tests.Biometrics，1954，10:417－451.

2.Armitage P.Tests for linear trends in proportions and frequencies.Biometrics，1955，11:375－386.

3.Gastwirth JL.The use of maximin efficiency robust tests in combining contingency tables and survival analysis.J.Amer.Statist，1985，80:380－384.

4.Podgor MJ，Gastwirth JL，Mehta CR.Efficiency robust tests of independence in contingency tables with ordered classifications.Stat Med，1996，15:2095－2105.

5.Bailer AJ，Portier CJ.Effects of treatment－induced mortality and tumorinduced mortality on tests for carcinogenicity in small samples.Biometrics，1988，44:417－431.

6.Bieler GS，Willians RL.Ratio Estimates，the Delta Method，and Quantal Response Tests for Increased Carcinogenicity.Biometrics，1993，49:793－801.

7.Kendall MG，Staurt A.The Advanced Theory of Statistics.London:Griffin，1979.

8.Gross ST.On asymptotic power and efficiency of tests of independence in contingency tables with ordered classifications.J Am Stat Assoc，1981，76:935－941.

9.Fleiss JL.Statistical Methods for Rates and Proportions.New York:Wiley，1981.

10.Graubar BI，Korn EL.Choice of column scores for testing independence in ordered 2 X K contingency tables.Biometrics，1987，43:471－476.

11.Van Ness PH，Holford TR，Dubin JA.Power simulation for categorical data using the RANTBL function.Pennsylvania，2005.

12.Chakraborti S，Schaafsma W.On the choice scores in contingency tables，1996，329－333.

13.Neuhäuser M，Hothorn LA.An exact Cochran－Armitage test for trend when dose－response shapes are a priori unknown.Comput Stat Data An，1999，30:403－412.