雨刮器非线性黏滑振动及其对刮刷效果的影响

张立军，黄 萌

（1.同济大学 汽车学院，上海201804；2.同济大学 新能源汽车工程中心，上海201804）

汽车雨刮器的作用是清除附着在挡风玻璃上的雨、雾、霜、雪、泥、尘埃及其他污物，保证驾驶员视野清晰，行车安全［1］.但是，如果雨刮器的结构设计、材料特性以及运行控制参数不合理，可能会恶化雨刮器的刮刷效果，损害视野.基于雨刮器的工作原理以及前期研究，雨刮器的刮刷效果会受到刮臂压紧力、刮片特性、玻璃表面形貌以及运行车速（导致空气动力学特性的改变）的影响［1－6］.因此，有关刮刷效果的控制主要从调整刮臂压紧力、攻击角等方面开展［2－3，5－6］.

实际上，在刮片对挡风玻璃刮拭时，刮片与玻璃之间的摩擦力的速度依赖性、非线性与时变特性是影响刮刷效果的根本原因.其中，由于摩擦系数—速度的负斜率特性所引起的刮臂或刮片黏滑振动可能会加剧刮刷速度的波动，从而在玻璃上产生刮痕残留，严重影响刮刷效果.目前，黏滑振动对于刮刷效果的影响尚未进行深入的研究与分析.为此，本文将建立雨刮器非线性动力学模型，通过数值计算的方法，利用分岔图和相轨迹分析刮刷过程中存在的黏滑振动现象及其与刮刷速度的关系；在此基础上，针对刮刷速度进行时间域和空间域的考察与评价，分析黏滑振动引起的刮痕的时空分布特性，并提出黏滑占空比和刮痕数量等指标，综合分析黏滑振动对刮刷效果的影响.本文的研究将为雨刮器的结构优化、刮刷速度控制、摩擦特性匹配提供基础理论依据，为改善刮刷效果提供指导.

1 雨刮器2自由度非线性动力学模型

［7］，建立雨刮器2自由度非线性动力学模型如图1所示.图1中，字母下标D 和P分别表示驾驶员侧和副驾驶员侧；LD，P表示刮臂无振动变形时的名义位置；lD，P为刮臂末端到刮臂安装孔中心的长度；ID，P表示刮臂总成的转 动惯量；KD，P和KM分别为两侧刮臂和雨刮器驱动电机输出端曲轴的扭转角刚度；CP，CDP为扭转角阻尼系数；MD，P为两侧刮片的摩擦阻力矩；ψD，P为两侧刮臂的名义输入角度；θD，P为刮臂的振动变形角，φD，P为两侧刮臂的总变形角度.

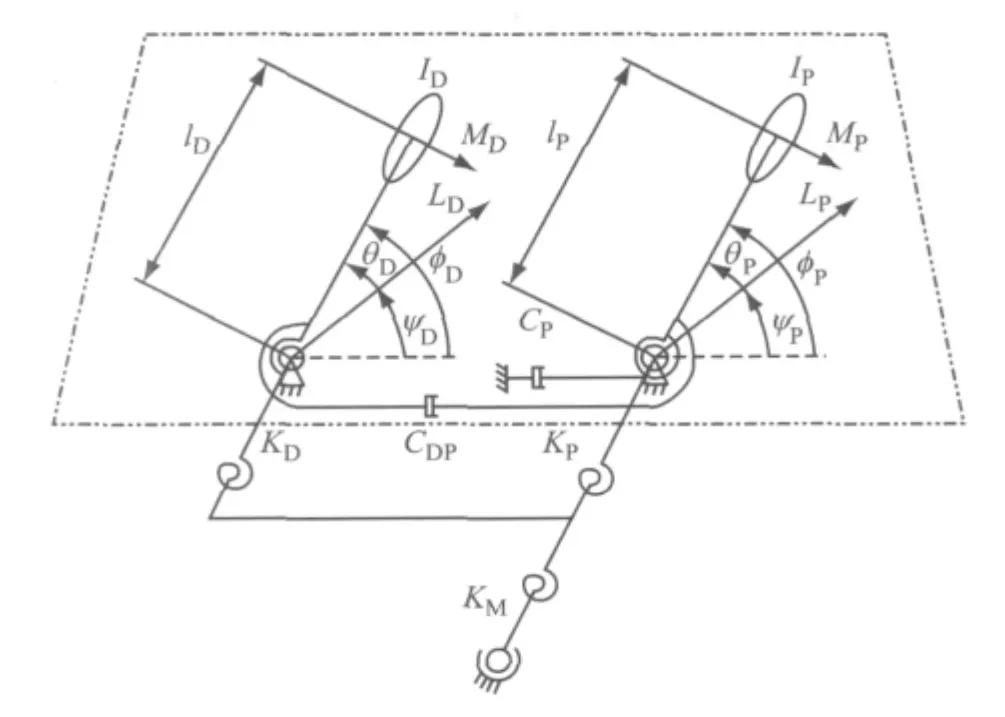
图1 雨刮器2自由度非线性动力学模型图Fig.1 Two DOF nonlinear dynamic model of wiper system

刮臂末端的名义线速度、实际线速度及刮臂振动变形线速度分别为

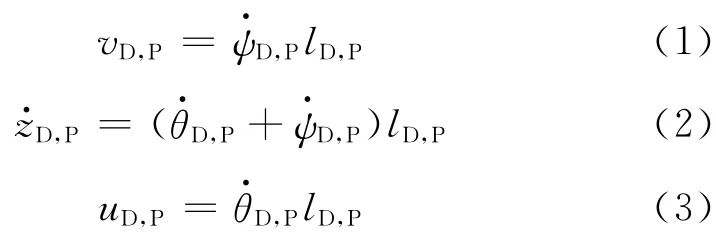
根据力学定律，建立两侧刮臂的运动微分方程为

式中：μ0 为雨刮器和挡风玻璃之间的静摩擦系数；RD，P和DD，P分别为弹性恢复力矩和阻尼力矩，其计算方法为

摩擦阻力矩的计算公式为

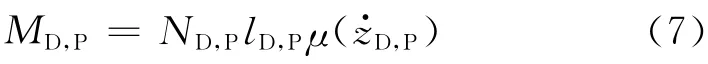
式中：ND，P表示两侧刮臂的法向压紧力为摩擦—速度特性，根据课题组的相关实验结果［4］得到摩擦—速度特性（见图2，详细的测试方法与结果参见文献［4］），并进行多项式数据拟合，得到其计算公式为

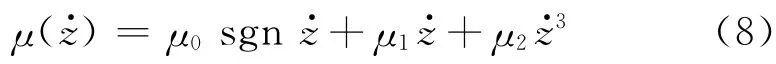
图2 摩擦—速度特性曲线Fig.2 Friction－velocity curve of wiper blade

2 雨刮器系统的非线性黏滑振动

根据所建立的2自由度系统模型，基于表1 所示的模型参数［7］，在Matlab／Simulink环境下进行雨刮器动力学特性的仿真，并利用达到稳定状态后的数值解进行分析［8］.参照文献［9－11］并依据实际常用的雨刮器的刮刷速度，选取名义刮刷速度vD的范围为0.1～0.8m·s－1.

表1 仿真分析用模型参数Tab.1 Model parameters for numerical calculation

2.1 黏滑振动现象

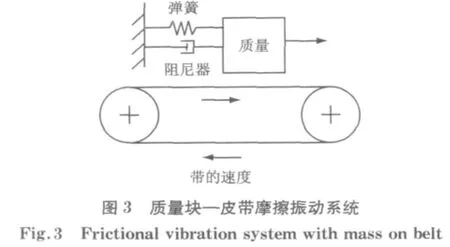
众所周知，在图3所示的典型的弹簧质量摩擦振动系统中，由于摩擦力和弹性恢复力之间平衡的建立与破坏循环发生，由此会导致质量块与皮带之间相对运动的不连续，即“黏滑振动”现象.研究认为，黏滑振动从根本上来说是由于摩擦系数—相对速度负斜率特性或者静摩擦系数和动摩擦系数的差别引起的［2，10，12］.图4为针对所研究的雨刮器对象在一定名义刮刷速度下计算得到的D 侧刮臂的运动相轨迹.显然，雨刮器在刮刷过程中发生了明显的黏滑振动现象

2.2 不同速度下的非线性黏滑振动

为了分析刮刷过程中黏滑振动的普遍存在性及刮刷速度对黏滑振动的影响，进行雨刮器非线性分岔特性的分析［8，13－15］.图5所示为D 侧刮臂变形角随名义刮刷速度的分岔特性，同时图中也显示了不同名义刮刷速度下的分岔运动特征.由图5可见：以vD＝0.485m·s－1为分界点，可将vD的取值区间划分为较低、较高刮速区.随着vD的降低，雨刮器高、低刮速区的黏滑振动形态变化过程均遵循：周期—准周期—混沌.在较高刮速区，还含有准周期和混沌交替出现的振动现象.当vD≥0.795m·s－1时，系统达到稳定状态，无自激振荡发生.显然，在所分析的刮刷速度区间内，刮臂变形角的幅值变化呈现出典型的非线性特征，因此其黏滑振动状态也会有所区别.进一步的分析表明：P 侧刮臂变形角随名义刮刷速度的分岔特性完全类似.

图5 D 侧刮臂变形角分岔图Fig.5 Bifurcation map of D－side wiper arm

2.3 刮刷速度对非线性黏滑振动的影响

下面进一步分析刮刷速度对黏滑振动特性的影响.根据图5所对应的各刮刷速度区间及运动特征，选取典型的名义刮刷速度值进行雨刮器系统D 侧刮臂的非线性黏滑振动的仿真计算，利用相轨迹（θDlD，进行分析.由计算得到的相轨迹（图6）分析可知：雨刮器刮刷过程中普遍伴随有显著的黏滑振动现象不同名义刮刷速度下黏着运动发生的具体空间位置及所对应的变形线位移的大小、滑动状态所对应的线速度区间均具有复杂的非线性特征；当系统处于周期Ⅱ区及非振荡区时，无黏滑振动现象，即提高名义刮刷速度vD有利于抑制黏 滑振动的发生.

图6 不同刮刷速度下的非线性黏滑振动的相轨迹Fig.6 Phase trajectories of nonlinear stick－slip motions under various wiper speeds

3 非线性黏滑振动对雨刮器刮刷效果的影响

雨刮器刮刷的非线性黏滑振动可能会引起挡风玻璃上残留刮痕，影响驾驶员的视野，危及行车安全，因此有必要从实际工程应用的角度就非线性黏滑振动对雨刮器刮刷效果的影响进行分析评价.在分析过程中，利用系统非线性黏滑振动仿真的稳态数值解，统一选取各典型刮刷速度下1s时间内刮臂末端实际线速度的时间历程及0°～60°刮刷角范围内刮臂实际角速度的等高线图，进行非线性黏滑振动的时空分布可视化分析.然后，采用黏着运动占空比定量分析黏着运动在整个刮刷速度区间的分布比重，并且对不同刮刷速度下残留的刮痕数目进行统计分析.

3.1 非线性黏滑振动的时空分布

规定刮臂单向刮刷角度范围为0°～150°，对应图6中各vD值，进行Matlab／Simulink环境下系统非线性黏滑振动的仿真，计算得到刮刷线速度的时间历程、实际刮刷角速度的等高线图汇总如图7 所示.时间历程图中，实际刮刷线速度时，刮臂处于黏着状态时，刮臂为滑动状态.与之相对应的等高线图中细窄的深灰色表示实际刮刷角速度为0，刮臂处于黏着状态，其余颜色表示刮刷角速度非0，刮臂处于滑动状态.

由图7进行定性分析可知：

（1）不同vD下，刮刷过程中普遍存在黏着运动和滑动运动的交替发生（如7a中标注所示），由此会在挡风玻璃上残留下一道道刮痕，刮痕的发生频度对应于黏着运动的发生频度.

（2）黏滑运动的发生及特征随着刮臂运动特征的不同，呈现不同的时间特点.当系统发生混沌运动时，黏着运动的发生时刻、持续时间及发生的频度带有明显的随机性；当系统发生准周期或周期运动时，黏着运动的发生几乎遵循周期性发生的规律；并且对应于同种振动状态，较高刮速区的黏着运动的发生频度明显小于较低刮速区的发生频度，但较高刮速区内每次黏着运动持续的时间相对于较低刮速区有所增长.

图7 刮刷黏滑运动的时间历程及空间分布图Fig.7 Time histories and contour maps of nonlinear stick－slip motions

（3）黏着运动引起的刮痕分布随着刮臂运动特征的不同，呈现不同的空间特点.当系统发生混沌运动时，黏着运动的发生空间位置和发生频度随机；当系统发生准周期或周期运动时，黏着运动的发生位置表现出周期性的特点.

3.2 刮刷效果评价与分析

为对非线性黏滑振动对雨刮器刮刷效果的影响进行定量分析，采用刮刷过程中黏着振动的占空比作为评价指标进行分析，并对150°的刮刷角范围内残留的刮痕数量进行统计.黏着运动的占空比反映了一定刮刷速度下黏着运动发生的频度.

图8为D，P两侧黏着运动所占的比重随着刮刷速度变化的情况.由图8分析可知：①当系统处于刮刷速度较低的混沌Ⅰ区及准周期Ⅰ区时，黏着运动的占空比最大，D，P 两侧分别接近37%和33%；随着vD的增大，占空比总体减小，但是在局部存在较为复杂的规律；在周期Ⅰ区，随着vD的增大，占空比单调减小；②当系统处于刮刷速度较高的混沌Ⅱ区时，D侧占空比随vD的增大而增大，在准周期Ⅱ区和周期Ⅲ区，占空比随vD的增大而单调减小；在整个较高刮速区，P侧占空比随vD的增大而减小，且P侧占空比明显低于D 侧占空比；③当vD＞0.725m·s－1时，D 侧占空比为0，无黏滑振动现象，类似地，当vD＞0.6m·s－1时，P侧占空比为0.

图8 黏着运动时间占空比Fig.8 Duty ratio of stick and slip motions

进一步从刮痕数量的角度分析不同刮刷速度下黏滑振动对刮刷效果的影响.图9所示为对150°的刮刷角范围内D，P两侧刮片导致的刮痕数量进行统计的结果.由图9可知：①低速段的刮痕数量总体上显著多于高速段；②在低速段的混沌Ⅰ区刮痕数量随着vD的增大而迅速减小；但是，在混沌Ⅰ区向准周期Ⅰ区过渡时，刮痕数量有明显的跃升现象；进入周期Ⅰ区后，刮痕数量随vD的增大而快速减小；③在低速段和高速段交接的区间，刮痕数量发生锐减现象；在高速段，刮痕数量随着vD的增大而减小，但D 侧减幅较小；④当vD＞0.6m·s－1时，P侧先于D侧（当vD＞0.725m·s－1时）进入无黏滑振动阶段，因此无刮痕产生；⑤在整个刮速区间内，P侧刮痕数量总体上少于D 侧.

图9 刮痕数量统计Fig.9 Quantity statistics of wiping scraping

根据图8和图9的结果进行综合分析发现，提高刮刷速度总体上可以有效抑制黏滑运动的发生频度并减轻驾驶员侧刮痕分布的不均匀性.但是，黏滑运动的时间占空比与刮痕数量并非呈正比例关系，亦非完全相关.这说明，雨刮器的黏滑振动的发生特性不仅受到刮刷速度的影响，而且也受到摩擦引起的非线性运动特性的强烈影响.

4 结论

（1）利用本文所建立的雨刮器摩擦振动非线性动力学模型能够分析摩擦引起的雨刮器非线性黏滑运动，所提出的时间占空比和刮痕数量统计方法能够体现黏着状态（刮痕发生）的时空分布特征，可以用于刮刷效果的定性和定量分析.

（2）雨刮器的黏滑振动表现出显著的刮刷速度依赖性，以及与不同速度下的混沌、准周期和周期运动的密切相关性；总体来说，增大刮刷速度有利于抑制、消除黏滑振动及其对刮刷效果的不利影响.

参考文献：

［1］ 德国BOSCH公司.汽车工程手册［M］.3版.魏春源，译.北京：北京理工大学出版社，2009.Bosch Germant.Handbook of automobile engineering［M］.3rd ed.Translated by WEI Chunyuan.Beijing：Beijing Institute of Technology Press，2009.

［2］ 柴苍修，吴金洲，田杰.挡风玻璃刮水器的摩擦特性［J］.汽车工艺与材料，1997（1）：7.CHAI Cangxiu， WU Jinzhou， TIAN Jie. Frictional characteristics of wiper and windscreen ［J］.Automobile Technology ＆Material，1997（1）：7.

［3］ 李军.全顺前风窗雨刮片刮净度提升的研究［D］.南京：南京理工大学机械工程学院，2007.LI Jun.Improvement of wiping clearity of Transit front wiper blade ［D］.School of Mechanical Engineering of Nanjing Technology University，2007.

［4］ 王小博.雨刮器刮刷过程摩擦振动分析［D］.上海：同济大学汽车学院，2008.WANG Xiaobo.Friction induced vibration of automotive wiper system［D］.Shanghai：College of Automotive Studies of Tongji University，2008.

［5］ Chevennement－Roux C，Régis Grenouillat，Dreher T，et al.Wiper systems with flexible structures—instabilities analysis and correlation with a theoretical model［C／CD］／／SAE Paper，［S.l.］：SAE：2005－01－2375.

［6］ Shigeki Okura，Tohru Sekiguchi.Dynamic analysis of blade reversal behavior in a windshield wiper system［C／CD］／／SAE Paper，［S.l.］：SAE：2000－01－0127.

［7］ Suzuki R，Yasuda K.Analysis of chatter vibration in an automotive wiper assembly［J］.JSME，1998，41（3）：616.

［8］ Stephen Lynch.Dynamical systems with applications using MATLAB［M］.Boston：Birkhäuser，2004.

［9］ Suzuki R，Yasuda K.Analysis of chatter vibration in an automotive wiper assembly（derivation of approximate solutions and study of vibration characteristics）［J］.JSME，1995，61（588）：3203.

［10］ Yukiho Murata，Yasuo Ohasi， Masaru Ishikawa，et al.Windshield wiper motor noise reduction［J］.Journal of Society of Automotive Engineers of Japan.1997，51（2）：24.

［11］ ZHENG Wang.Control of chaotic vibration in automotive wiper systems［J］.Chaos，Solitons and Fractals，2009，39：168.

［12］ 丁文镜.自激振动［M］.北京：清华大学出版社，2009.DING Wenjing.Self excited vibration［M］.Beijing：Tsinghua Univeristy Press，2009.

［13］ Tomasz Kapitaniak.Chaos for engineers，theory，applications and control［M］.2nd ed.Berlin：Springer－Verlag，2000.

［14］ 刘秉正，彭建华.非线性动力学［M］.北京：高等教育出版社，2004.LIU Bingzheng，PENG Jianhua.Nonlinear dynamics［M］.Beijing：Higher Education Press，2004.

［15］ 刘延柱，陈立群.非线性振动［M］.北京：高等教育出版社，2001.LIU Yanzhu，CHEN Liqun.Nonlinear vibration［M］.Beijing：Higher Education Press，2001.