内衬混凝土波折钢腹板梁抗弯性能试验研究

王达磊，贺 君，2，陈艾荣，刘玉擎

（1.同济大学 土木工程学院，上海200092；2.早稻田大学 土木与环境工程学院，东京1698555）

波折钢腹板组合梁作为一种新型钢 混凝土组合结构，以折叠形钢腹板代替了传统混凝土腹板和平钢腹板，具有自重轻、跨越能力大、受力明确、避免腹板开裂等突出优点［1］.目前，国内外相关研究机构对其抗弯、抗剪、抗扭、变形和徐变等基本力学性能进行了理论和试验研究［2－8］.通常设计中弯曲、剪切承载力分别通过混凝土顶、底板及波折钢腹板截面承担.但是，大、中等规模的连续梁与刚构桥，中支点附近弯矩和剪力均为极大值，且该区域构造及约束条件复杂，使得各构件相互影响处于复合应力状态.并且波折钢腹板纵向刚度相对较小，其剪切变形显著，在中支点位置受到混凝土顶、底板及横隔梁的约束，混凝土顶、底板连接处产生局部应力.因此，提出波折腹板内侧浇筑混凝土，采用焊钉及与翼缘焊接的钢筋网进行完全连接形成组合结构改善受力性能（图1），既可以提高波折腹板抗屈曲性能，同时又能够借助内衬的混凝土构造，使腹板的作用力有效地传给桥墩.根部截面高度达到7m 或以上的几座已建波折腹板连续刚构桥基本上都采取了该措施，即在距离根部一定范围内的波折腹板内衬混凝土［1，9］.

目前，对于波折钢腹板内衬混凝土组合结构没有明确的设计方法，且内衬混凝土对组合结构承载性能及变形能力的影响研究较少，因此本文通过波折钢板－内衬混凝土组合梁弯曲性能试验，研究波折钢板－内衬混凝土组合结构的破坏模式以及受力特点.提出并验证波折钢腹板－内衬混凝土组合构造的弯曲强度计算模型，完善波折钢腹板组合桥梁设计理论与方法.

图1 波折腹板内衬混凝土组合梁Fig.1 Concrete－encased composite girder with corrugated web

1 弯曲性能试验

1.1 试验模型概况

设计波折腹板钢梁（BS－1）及其内衬混凝土组合梁（BC－1）模型，试件总长3.94m，梁高0.44m.钢梁腹板、翼缘板采用Q370qENH耐候钢，屈服强度与极限强度分别为384 MPa与460 MPa.其中翼缘宽度300mm，厚度20mm；波折腹板高度400mm，厚度10 mm，波长为560 mm，平板及斜板长度均为150mm.内衬混凝土（标号为C50）实测轴压强度与弹性模量分别为54.8 MPa与49.4GPa，其内部布置直径D为8mm 的HRB335螺纹钢筋网.钢腹板与内衬混凝土之间通过圆柱头铆螺钢焊钉连接，其直径为16mm，高度选用80mm，型号为ML15.试件整体布置以及具体尺寸如图2所示.

1.2 加载与测试装置

试验通过两点对称加载研究波折钢板－内衬混凝土组合梁弯曲性能，如图3 所示.试件距离梁端150mm 位置安装滚动支座；跨中710mm 范围通过分配梁两点加P／2集中力荷载，试件剪跨比为3.33，实现跨中区域纯弯状态.支点和加载区域设置竖向加劲肋防止组合梁局部受力破坏.试验采用伺服加载系统对分配梁跨中进行分阶段逐级加载，第1 阶段通过力控制加载至钢结构屈服；第2阶段通过位移控制加载至结构破坏.

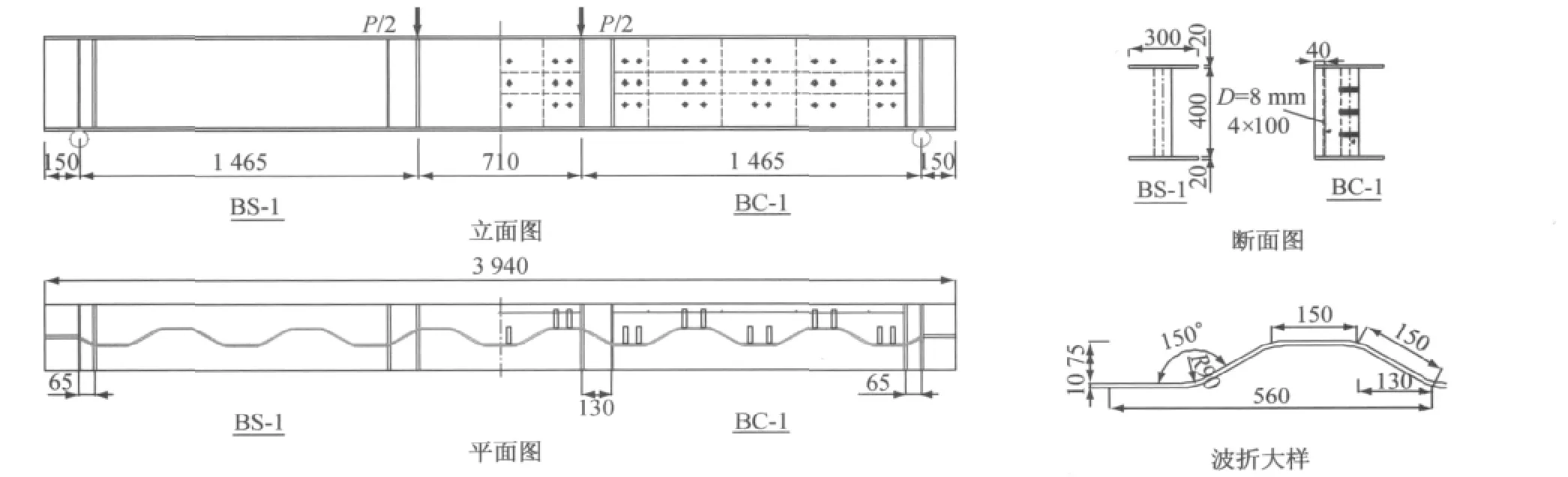
图2 试件概况（单位：mm）Fig.2 Outline of test specimen（unit：mm）

图3 加载状态Fig.3 Test setup

加载过程中，通过钢结构、混凝土及钢筋表面布置应变片测试关键部位腹板、翼缘以及内衬混凝土的应变分布.组合梁底部以及侧面安装位移计监测加载过程组合梁面内以及面外的挠曲过程.同时，观察纯弯区域内衬混凝土裂缝的发生、开展及贯通情况，记录混凝土裂缝宽度变化.

2 试验结果及分析

2.1 承载能力与破坏模式

图4 为试件跨中截面荷载—位移曲线.对于波折腹板钢梁，受压翼缘屈服前，跨中竖向位移随荷载线性变化，随后压缩翼缘进入塑性，当荷载达到极限状态，翼缘屈曲的同时腹板产生面外变形（图5a），由于波折腹板几乎不参与抗弯，因此翼缘完全塑性屈曲后，荷载迅速下降.而腹板内衬混凝土之后，同样受压翼缘屈服前，跨中竖向位移随荷载线性变化，随后压缩翼缘屈服，由于内衬混凝土的约束，翼缘塑性强化阶段并不会马上屈曲，荷载继续增加直到受压区域混凝土达到极限抗压强度，此后受压翼缘屈曲，内衬混凝土厚度较小截面压碎.由于混凝土单面内衬，组合截面纵向非对称，导致最终产生侧向扭转，跨中腹板面外变形最大10 mm，如图4 与图5b 所示.

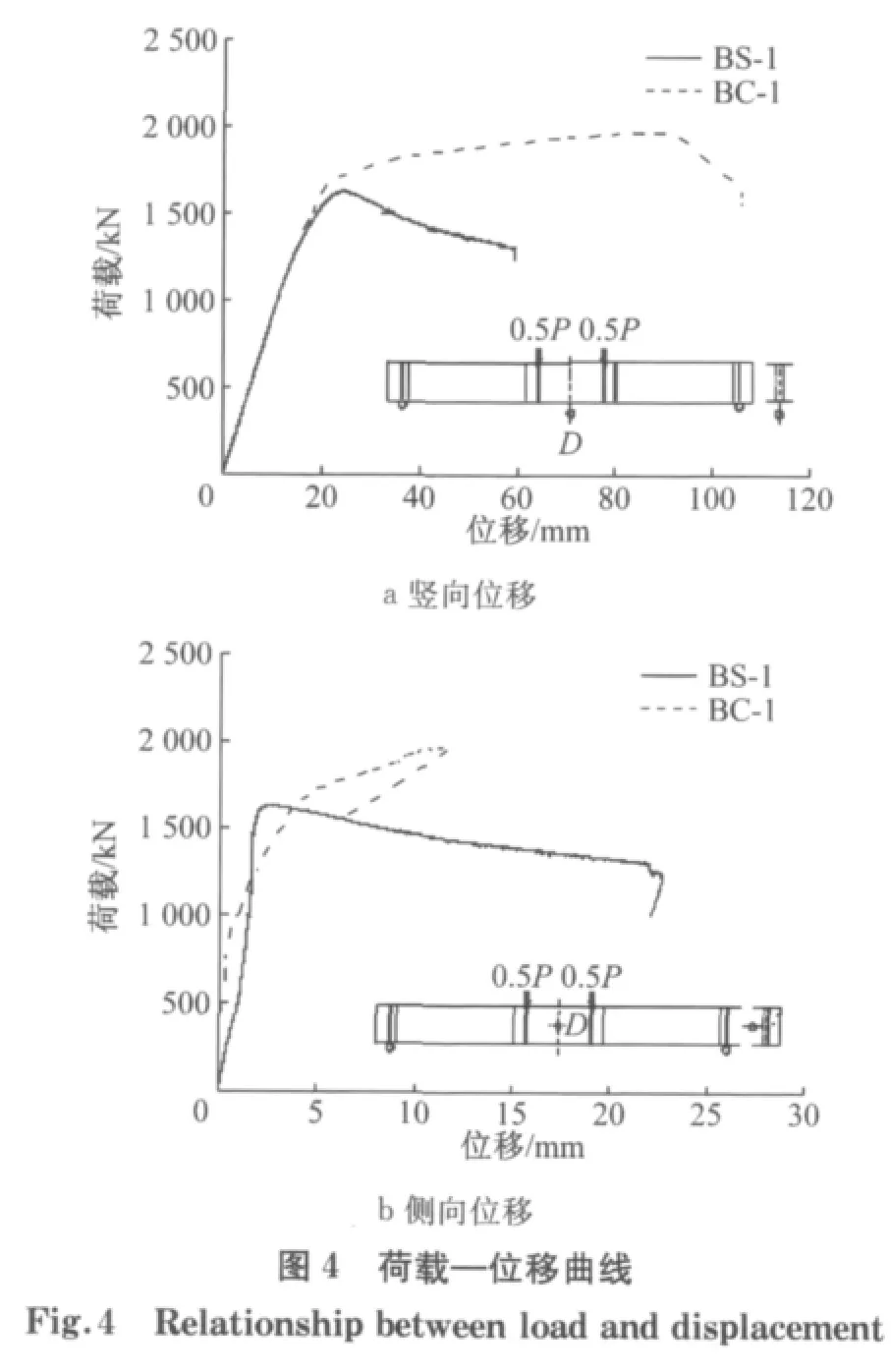
表1 为试件初始开裂、翼缘屈服和极限状态3个阶段承载能力以及相应变形的试验结果.波折腹板与内衬混凝土通过焊钉连接共同作用，受压翼缘屈曲破坏由于内衬混凝土限制而推迟，同时受压区混凝土承担部分荷载，因此，同波折腹板钢梁相比，组合梁承载能力提高21%，极限强度对应的位移增加到原来的3.58倍，延性得到很大的提高.

表1 试件承载能力Tab.1 Loading capacity of test specimen

2.2 裂缝扩展模式

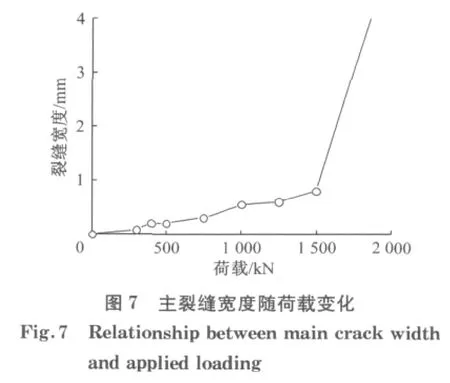
图6为试件BC－1纯弯区域内衬混凝土裂缝出现及发展的过程.当荷载处于125kN 左右，试件跨中下翼缘内衬混凝土出现竖向微裂缝，随着荷载增加，裂缝沿梁高方向由底部向顶部延伸.加载点附近由于内衬混凝土厚度较小，竖向裂缝较为集中；极限状态时，竖向裂缝贯穿整个梁高，受压区混凝土达到极限抗压强度破坏.图7为BC－1试件的主裂缝宽度随荷载变化情况，翼缘屈服前裂缝宽度基本线性增长，其小于0.5mm；极限状态宽度急剧增加，破坏时最大宽度超过4mm.

2.3 应变分布

试件跨中截面翼缘布置纵向应变计测试弯曲应力，图8为试件BS－1与BC－1钢翼缘正应变随荷载变化，翼缘屈服前弯曲正应变随荷载线性增加，当受压应变达到3 000×10－6之后，BS－1受压翼缘远离腹板的较大宽度悬臂端发生屈曲，应变迅速增加.而BC－1由于内衬混凝土限制该侧翼缘变形，当受压应变达到4 000×10－6左右，非内衬侧较小宽度悬臂端发生屈曲，引起内衬侧翼缘逐渐脱离混凝土，但是受压应变随荷载继续增加；而受拉翼缘应变在上翼缘屈曲后仍继续增加，直到混凝土压碎结构破坏.

图9为试件不同荷载等级，跨中截面钢梁与内衬混凝土表面弯曲应变沿梁高方向分布.波折腹板钢梁BS－1试件，腹板由于轴向刚度低，弯曲荷载作用能够自由变形，除与翼缘连接部位外整个梁高腹板正应变均很小，上、下翼缘屈服前的压应变与拉应变几乎相等，中性轴几乎位于腹板的中央.内衬混凝土波折腹板组合梁BC－1，受压区钢腹板与内衬混凝土两者通过焊钉完全连接，在相同荷载等级（混凝土达到极限强度前）应变基本相等，而受拉区混凝土开裂后退出工作，波折腹板靠近下翼缘附近位置产生部分应变，尤其是下翼缘屈服之后.BC－1 的中性轴由开裂前的中央位置逐渐上升，当作用荷载为1 500 kN 时，中性轴约距梁底250mm.

3 理论计算模型

3.1 波折腹板钢梁

一般I 型钢梁弯曲强度设计，规范（加拿大CSA 2002［10］，美国AISC 2003［11］）通过限制翼缘以及腹板的宽厚比，在屈服弯矩与塑性弯矩达到之前防止出现翼缘或腹板局部屈曲.AISC－LRFD［11］完全塑性及非完全塑性（满足屈服）截面翼缘与腹板宽厚比限制如下：完全塑性截面

非完全塑性截面

式中：bfl，tfl分别为 受 压 翼 缘 的 宽 度 与 厚 度；hw，tw分别为腹板的高度与厚度；E，Fy分别为钢结构的弹性模量及屈服强度；σr为残余应力，热轧加工取65 MPa，焊接制作取114 MPa.

对于波折腹板钢梁，波折腹板由于波高hr影响，翼缘悬臂长度沿梁长不等，因此翼缘悬臂宽厚比也非固定值，翼缘悬臂bc如图10所示，腹板水平折板对应的最大与最小翼缘悬臂为

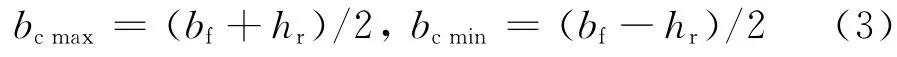
Johnson［12］通过研究得到当R＜0.14，R为面积EFGH与ABCD的比值，bc取平均值bcav，当R＞0.14，偏于安全考虑bc采用最大值bcmax.其中，σx为受压翼缘应力；bf为翼缘宽度；a，b分别为波折腹板斜板及平板的长度；d为斜板的水平投影长度；hr为波折高度，如图10所示.

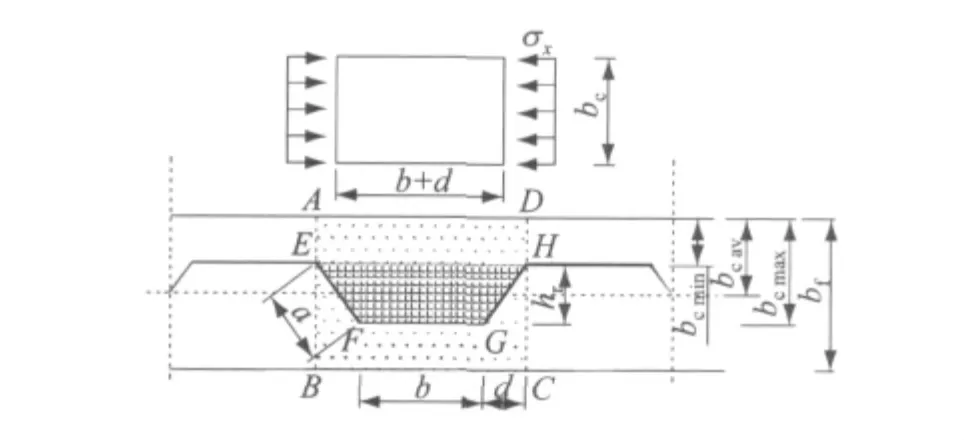
图10 受压翼缘悬臂部分Fig.10 The cantilevered part of compressive flange

试验结果及以往Abbas［13］与Sayed－Ahmed［14］研究结果表明，波折腹板钢梁抗弯承载力仅依靠上、下翼缘承担，不考虑腹板作用.因此，波折腹板梁面内弯曲承载能力如下：

式中：Ff为翼缘屈服应力；Weff为不考虑腹板作用的有效截面系数，依据规范限制要求取屈服截面或完全塑性截面.

3.2 内衬混凝土波折腹板组合梁

依据波折钢板－内衬混凝土组合梁弯曲荷载作用，钢结构与内衬混凝土破坏模式及其应力状态，对抗弯强度计算模型进行假设：①极限状态上、下翼缘钢板达到极限强度；②受压区混凝土与钢腹板完全连接，共同承担弯矩，混凝土及钢腹板受压区正应力沿高度方向由翼缘至中性轴线性递减；③受拉区混凝土达到极限拉应力后退出工作，同翼缘连接区域部分波折腹板拉应力达到屈服.

选取抗弯强度最不利的混凝土厚度最小截面（C－C）为分析对象，推导波折钢板－内衬混凝土组合梁的抗弯承载能力，参见图11.

图11 波折钢板内衬混凝土组合截面Fig.11 Composite section of concrete encased girder with corrugated web

试验中完全剪力连接的波折钢板 内衬混凝土组合梁弯曲强度可以通过组合截面每一部分的合力确定，如内衬混凝土板与波折钢板.极限状态下，组合截面的应力σ及内力F分布如图12所示.图中，h1为中性轴至顶端距离，h2为受拉区波折钢板屈服范围.受压区混凝土及波折钢板正应力线性变化，受拉区波折钢板应力屈服，根据应力分布得到的内力状态，Pc为混凝土压力；Pfc，Pft分别为翼缘压、拉力；Pwt，Pwc分别为波折钢板拉、压力.因此中性轴通过力的平衡方程得到

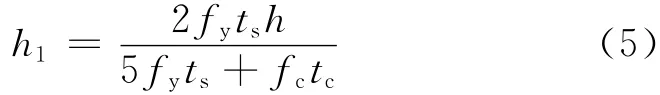
式中：fy，fc分别为钢板屈服应力及混凝土标准抗压强 度；ts，tc分 别 为 钢 腹 板 及 内 衬 混 凝 土 厚 度；h为 梁高.

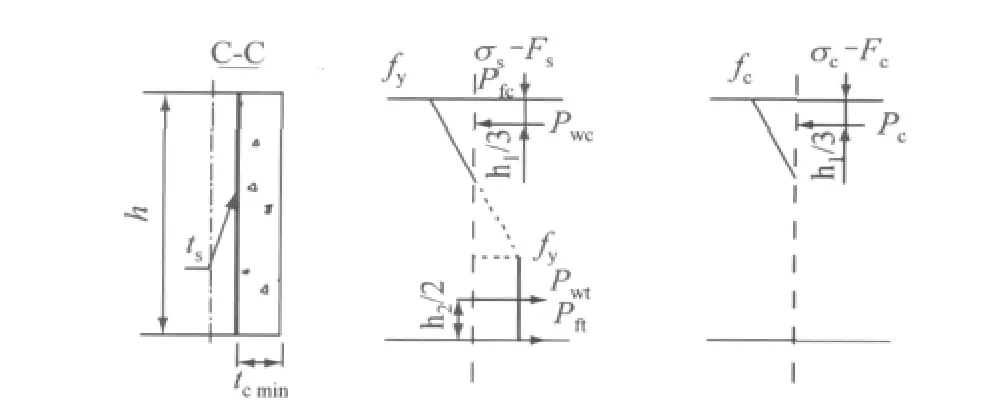
图12 组合截面应力分布及受力状态Fig.12 Stress distribution and force state of composite section

完全剪力连接情况，波折钢板内衬混凝土组合截面弯曲强度Mbc，通过两者的内力分布推导

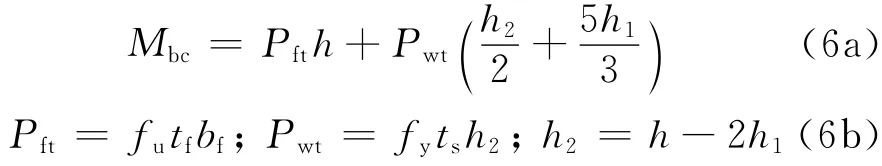
式中：tf，bf分别为翼缘厚度及宽度.翼缘受到混凝土的约束极限状态应力达到极限应力fu.

翼缘屈服对应的波折钢板－内衬混凝土组合梁弯曲强度计算方法类似，由于内衬混凝土受压抵抗弯矩，中性轴位置随荷载由截面中央逐渐上升，通常受拉下翼缘首先屈服（达到屈服应变εy），依据内力平衡得到中性轴位置，以及上翼缘钢梁与混凝土最大应变εT，按照材料本构关系得到相应的应力，最终基于应力分布得到受力状态及屈服弯矩.

表2为试件屈服以及极限弯矩对应的试验与计算结果比较，弯曲强度计算值同试验结果相比吻合较好，可以采用本文提出的计算模型初步估计波折钢板－内衬混凝土的弯曲强度.

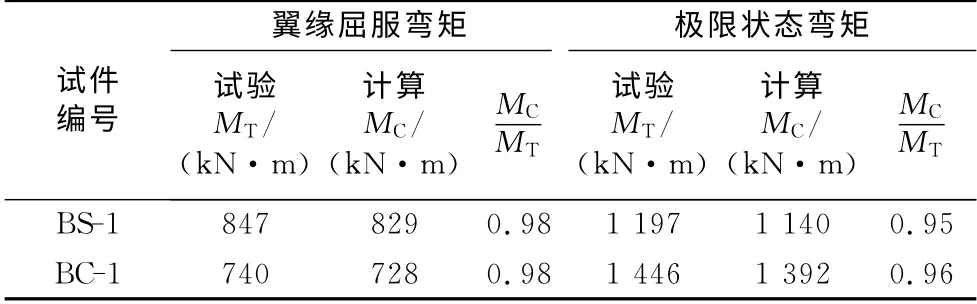
表2 承载能力试验与计算比较Tab.2 Comparison of the bearing capacity between the experimental and the calculated results

4 结论

本文提出波折腹板内衬混凝土改善负弯矩区结构的力学性能.通过弯曲荷载作用模型试验研究波折腹板内衬混凝土组合梁的受力机理，得到相关结论如下：

（1）波折腹板内衬混凝土组合梁，受压翼缘屈曲破坏由于内衬混凝土限制而推迟，同时受压区混凝土承担部分荷载，因此同波折腹板钢梁相比，组合梁承载能力提高21%，极限强度对应的位移增加到原来的3.58倍，延性得到大大的提高.

（2）波折腹板钢梁弯曲荷载作用，腹板除与翼缘连接部位外整个梁高正应变均很小，因此可以忽略腹板抗弯贡献.内衬混凝土波折腹板组合梁，受压区钢腹板与内衬混凝土通过焊钉完全连接，在相同荷载等级两者应变基本相等，而受拉区混凝土开裂后退出工作，因此内衬混凝土后受压区的波折腹板可以承担部分弯矩作用.

（3）依据波折钢板－内衬混凝土组合梁弯曲荷载作用，钢梁与内衬混凝土破坏模式及其应力状态，提出弯曲强度的计算方法，并通过试验结果验证，两者吻合较好，可以采用本文提出的计算模型初步估计波折钢板－内衬混凝土的弯曲强度.

［1］ 刘玉擎.组合结构桥梁［M］.北京：人民交通出版社，2005.LIU Yuqing.Steel－concrete hybrid bridge［M］.Beijing：China Communications Press，2005.

［2］ 贺君.波折钢腹板组合桥梁力学性能与设计方法研究［D］.上海：同济大学土木工程学院，2011.HE Jun. Mechanical performance and design method of composite bridge with corrugated steel webs［D］.Shanghai：College of Civil Engineering of Tongji University，2011.

［3］ Elgaaly M，Seshadri A，Hamilton R W.Bending strength of steel beams with corrugated webs［J］.Journal of Structural Engineering，1997，123（6）：772.

［4］ HE Jun，LIU Yuqing，CHEN Airong.Elastic bending theory of composite bridge with corrugated steel web considering shear deformation［J］.Key Engineering Materials，2009，400－402：575.

［5］ Sause R， Braxtan T N.Shear strength of trapezoidal corrugated steel webs ［J］.Journal of Constructional Steel Research，2011，67：223.

［6］ Mo Y L，Fan Y.Torsional design of hybrid concrete box girders［J］.Journal of Bridge Engineering，2006，11：329.

［7］ 贺君，刘玉擎，陈艾荣，等.折腹式组合梁桥考虑剪切变形的挠度计算［J］.同济大学学报：自然科学版，2009，37（4）：440.HE Jun，LIU Yuqing，CHEN Airong，et al.Deflection calculation of composite girder bridge with considering shear deformation ［J］.Journal of Tongji University：Natural Science，2009，37（4）：440.

［8］ Maeda H，Sakai H，Komiya M.Study on creep analysis method of steel－concrete mixed girders with corrugated steel web［J］.Proceeding of JSCE，2003，725：171.

［9］ Nakamura S，Narita N.Bending and shear strengths of partially encased composite I－girders ［J］. Journal of Constructional Steel Research，2003，59（12）：1435.

［10］ Canadian Standards Association.CAN／CSA－S16.1－02 Limit states design of steel structures. Mississauga：Canadian Standards Association，2002.

［11］ American Institute of Steel Construction Manual Committee.Manual of steel construction：load and resistance factor design［M］.3rd ed.Illinois：AISC，2003.

［12］ Johnson R P，Cafolla J.Local flange buckling in plate girders with corrugated webs［J］.Structures and Buildings，1997，123：148.

［13］ Abbas H H.Analysis and design of corrugated web I－girders for bridges using high performance steel［D］.Bethlehem （PA）：Department of Civil and Environmental Engineering of Lehigh University，2003.

［14］ Sayed－Ahmed E Y.Design aspects of steel I－girders with corrugated steel webs［J］.Electronic Journal of Structural Engineering，2007，7：27.