大跨度钢斜拉桥施工过程线形控制

吴 杰，罗晓群，张其林

（同济大学 土木工程学院，上海200092）

自瑞典于1955年建造第一座斜拉桥以来，由于其良好的结构性能和跨越能力以及优美的建筑造型，使得现代斜拉桥在世界范围内得到了迅速的发展［1－3］.由于斜拉桥结构的受力特点，在跨度大于500 m 以上的斜拉桥中通常采用钢主梁形式，如日本多多罗大桥（主跨890m）、法国诺曼底大桥（主跨856 m）和中国苏通大桥（主跨1 088m）的主跨主梁结构均采用钢箱梁形式.斜拉桥是柔性高次超静定结构，具有强烈的几何非线性行为，主要表现在［4－5］：①斜拉索垂度效应；②桥塔和主梁的梁柱效应；③结构大位移效应.大跨钢斜拉桥的特性决定了施工控制是其成功建造的关键因素之一.国内外许多学者都研究了桥梁的施工控制问题［6－8］，比如，Manabe在多多罗大桥中提出了精度控制的概念，李乔等在大跨度斜拉桥控制中应用了几何自适应控制技术，张建民和肖汝诚从索力优化和线形控制两方面对大跨度斜拉桥进行双控控制.研究表明，大跨钢斜拉桥由于主梁相对较柔，施工期间的主梁标高变化幅度非常大，因此施工过程中的线形控制就是一个十分关键的问题［7］.

大跨钢斜拉桥由于几何非线性的影响，其施工计算与结构各节段的初始安装位置密切相关，安装位置不仅影响最终线形也影响成桥内力，而安装位置是由正装计算累计变形量反算出来的，因此施工线形的求解是一非线性过程.目前针对斜拉桥的施工线形控制研究主要是基于国外通用有限元分析软件或桥梁专用分析程序，如ANSYS，Sap 2000，MIDAS和TDV 2000 等［7－9］.这 些 软 件 无 法 考 虑 施工过程新增构件的不同激活方式，不能直接进行考虑几何非线性的施工过程线形控制分析.本文采用多段短索桁架单元模拟长索的非线性效应，通过改变单元的无应力长度实现索的多次张拉，采用增量的Updated Lagrange（U.L.）列式模拟梁柱效应，有效地解决了大跨度钢斜拉桥施工过程中的几何非线性和索的多次张拉问题；提出施工过程新构件激活的3种方式，考虑非线性多次迭代计算出构件安装过程中的实际位置，使斜拉桥施工完成后的线形和初始设计线形一致.基于以上原理编制了大跨度钢斜拉桥非线性分析及施工过程线形控制模拟软件BINAS，苏通大桥工程算例验证了本文方法的有效性.

1 斜拉索多次张拉的处理

采用多段只受拉桁架单元模拟斜拉桥中的长索效应，考虑到软件使用便捷性问题，用户定义截面、材料和索力等构件特性时仍按整个长索定义，程序内部自动将其分割为多个单元.由于索的应力刚度矩阵是以无应力状态的长度L0为基准的，而计算时的设计长度实际上包含了初应力的影响，因此需要由构件的内力求出无应力长度.为调整斜拉桥结构的受力状态，施工过程中可能对索实施多次张拉，这一过程可以用以下方法进行模拟：

（1）假设第1次张拉时索两端的节点为k1，k2，定义第1次张拉索力为P1，物理意义表示如果节点k1，k2坐标不变，索内拉力为P1.此时可以通过计算原长l01实现拉力¯P1＝P1，当前几何长度l1为节点k1，k2间的距离，假设材料处于弹性阶段，E为材料的弹性模量，A为截面面积，则原长可表示为

以l01为原长，按非线性计算可以得到当前状态下索的实际拉力P1，同时改变坐标得到新的节点位置k′1，k′2.

（2）第2 次定义索力增量P2，物理意义表示如果节点坐标不变，索内拉力为¯P2＝P′1＋P2，再次改变原长l02实现¯P2，当前的几何长度l2为坐标更新后的节点k′1，k′2间的距离.将式（1）中的¯P1用¯P2代替，可以求出此时的原长l02，再按非线性计算可以得到当前状态下索的实际拉力P′2.重复上述步骤，可以实现索的多次张拉.

2 施工过程线形控制原理

2.1 施工过程跟踪计算方法

斜拉桥施工过程中，已建成的老构件在自重及各种荷载作用下将产生一定的变形和位移而偏离原有坐标位置，如果施工时的新构件仍按照原有坐标对接，将会产生额外的线位移误差.因此在施工过程分析中，新增构件和节点的起始坐标必须以当前阶段计算所得的结构几何为依据进行构筑，而不能简单地套用原始设计中构件和节点的坐标.根据新激活构件的安装方式，本文提出将施工过程分析模型分为3类：切线安装、平行安装和建模位置安装.其中切线安装和平行安装用于施工过程分析，模拟施工过程中新增构件的不同安装方式；建模位置安装用于施工过程线形控制分析，通过非线性迭代计算得到安装线形.以悬臂梁为例，假设设计线形是水平的，非线性分析中新构件的3种激活方式如图1所示.

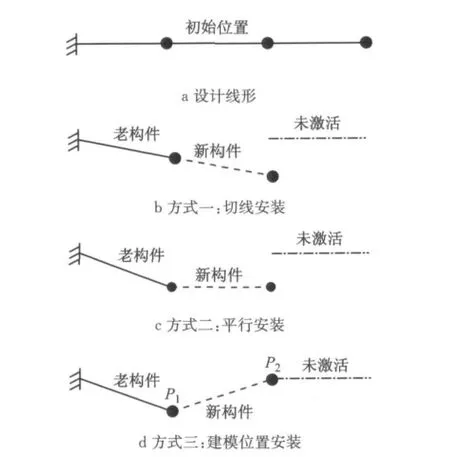
图1 新构件的3种激活方式Fig.1 Three activated modes of new elements

2.1.1 切线安装

新构件激活时考虑节点转角，用于模拟本施工步的新增构件相切于已变形构件的端部，如图1b所示.设构件MN是长度为L的新构件，MN与x轴夹角为ω（图2），当老节点M产生刚体位移u（M），v（M）和刚体转角θ（M）时，新节点N的总初始位移为［10］

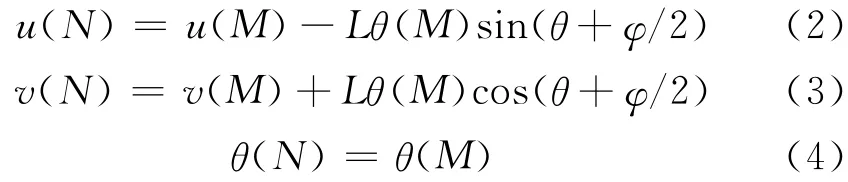
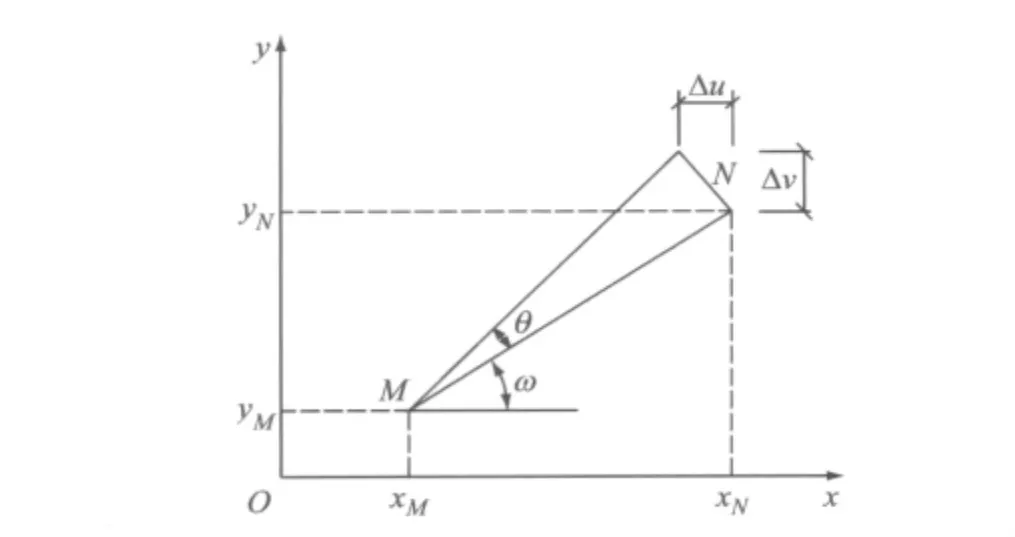
图2 新节点初始位移示意图Fig.2 Initial displacement of new nodes

2.1.2 平行安装

新激活构件按建模位置平行安装到已激活构件端部，如图1c所示.将切线模型中的θ角设为0，此时

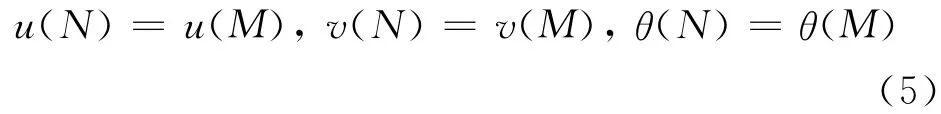
2.1.3 建模位置安装

新构件激活时，前一步已激活的端部节点P1按变形后的位置确定，新激活的端部节点P2位置为模型坐标，如图1d所示.

设第i个施工阶段结束时的几何线形可用轴线坐标xi，yi和φi表示，第i＋1施工阶段的位移（包括新节点初始位移）为ui＋1，vi＋1和θi＋1，则第i＋1施工阶段结束时的几何线形为

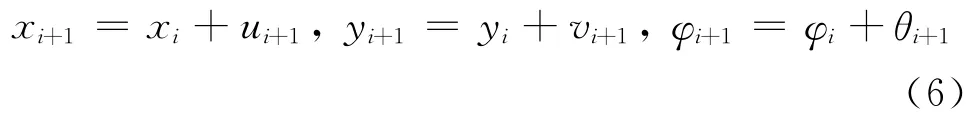
在更新后的位置上作几何非线性施工过程分析，可以得到各施工步下的节点位移和构件内力，为后续的线形控制分析做准备.

2.2 线形控制计算方法

本文的主要目的是通过施工控制模拟分析，使斜拉桥施工完成后的线形和初始设计线形一致，见图3.

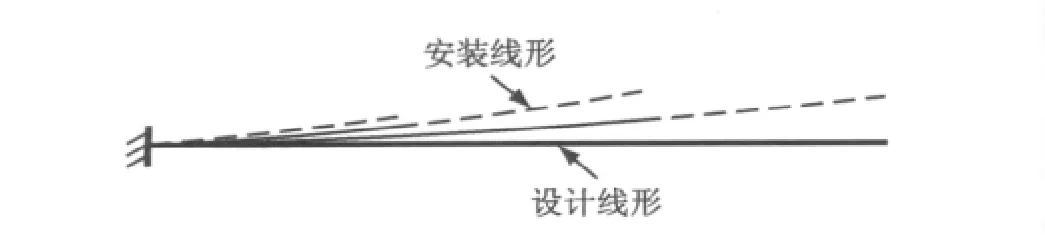
图3 安装线形和设计线形示意图Fig.3 Installation and design linetype

施工过程线形控制分析的原理是：先按平行安装或切线安装模型作1次正向的施工过程分析，根据计算结果将节点坐标反拱后按建模位置模型再作施工过程分析，如此反复，直到满足设计线形位置为止.线形控制计算步骤如下：

（1）按斜拉桥的设计线形建立施工过程计算模型；

（2）按平行安装或切线安装模型作施工过程分析，记录第i个施工阶段节点j的增量位移ΔUij；

（3）假设当前为第k个施工步，计算新激活节点的反拱值其中n为总施工步数；（4）激活新构件，老节点坐标为上一步结束时的位置，修正新激活节点坐标为建模位置减去

（5）k从1到n循环，得到第1次反拱后的斜拉桥主梁线形；

（6）按更新后的节点坐标进行施工过程非线性分析，如果分析完成后的线形与设计线形的误差超过规定的限值，则将差值作为反拱值，再次作非线性施工过程分析，直到满足规定的精度为止；

（7）按空间坐标计算新激活构件与已激活构件的夹角，同时记录构件端点的空间坐标，计算出构件的安装线形.

3 施工过程线形控制模拟软件

基于以上原理，以AutoCAD 为开发平台，运用ObjectARX 和Visual C＋＋等开发工具实现了大跨钢斜拉桥非线性分析及施工过程线形控制模拟软件——BINAS（图4）.软件具有强大的几何非线性分析功能，包括斜拉索非线性、重力二阶效应（P—Δ效应）、大位移大转角效应等；实现了多次无应力索长张拉，考虑非线性多次迭代计算预拱度，自动计算节段拼装线形等功能，大幅度减少了施工控制阶段的计算分析工作量.目前软件不考虑混凝土收缩徐变与结构几何非线性的耦合计算.

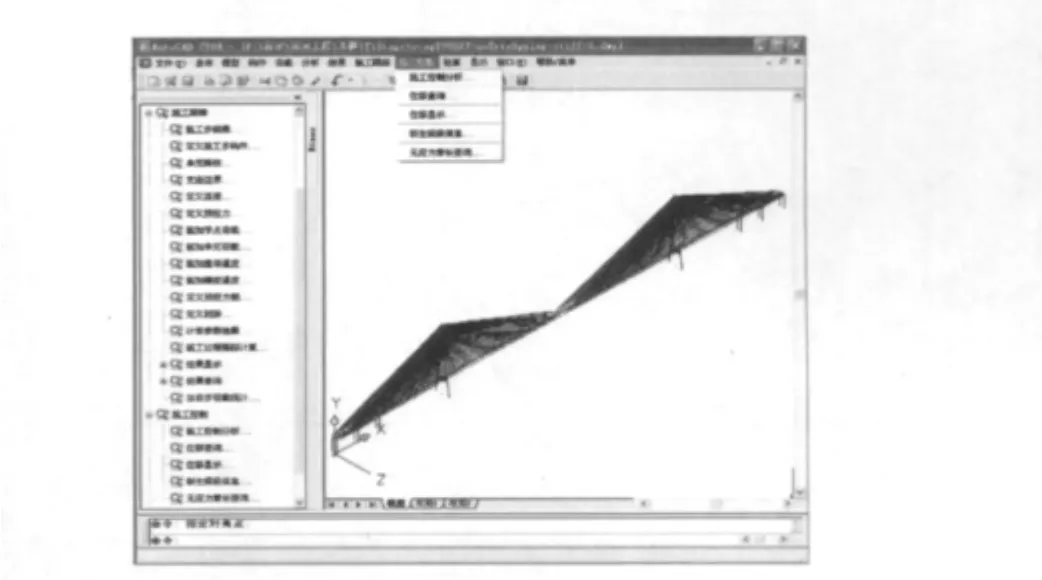
图4 BINAS软件主界面Fig.4 Main interface of BINAS software

在非线性分析中，由于多次总刚组装和分解，使得有限元方程的分解过程成为制约整个求解速度的瓶颈.BINAS采取大型稀疏矩阵求解方法，首先通过一个模拟定序算法确定较佳的消去顺序；然后为了尽可能减少在分解过程中的元素查找，采用符号的不带平方根的乔列斯基LDLT分解方法记录下总刚修改顺序；最后进行数值的LDLT分解和求解.稀疏矩阵求解器可大大节省机器内存，提高运算速度.

4 算例

4.1 斜拉悬臂梁结构

斜拉悬臂梁结构如图5所示.主梁截面：矩形1 m×5m，面积A＝5.0m2，惯性距I＝0.416 7m4.索截面：直径0.1m，面积A＝0.007 853m2，惯性距I＝4.909×10－6m4.材料：梁混凝土标号为C50，弹性模量E＝34.5GPa.索为钢材Q235，弹性模量E＝206GPa；不考虑构件自重.施工过程见图6.各施工步骤分别为：①安装梁段B1，在右端施加节点荷载1 000kN；②安装拉索C1，施加索力2 000kN；③安装梁段B2，在右端施加节点荷载1 000kN；④安装拉索C2，施加索力2 000kN.

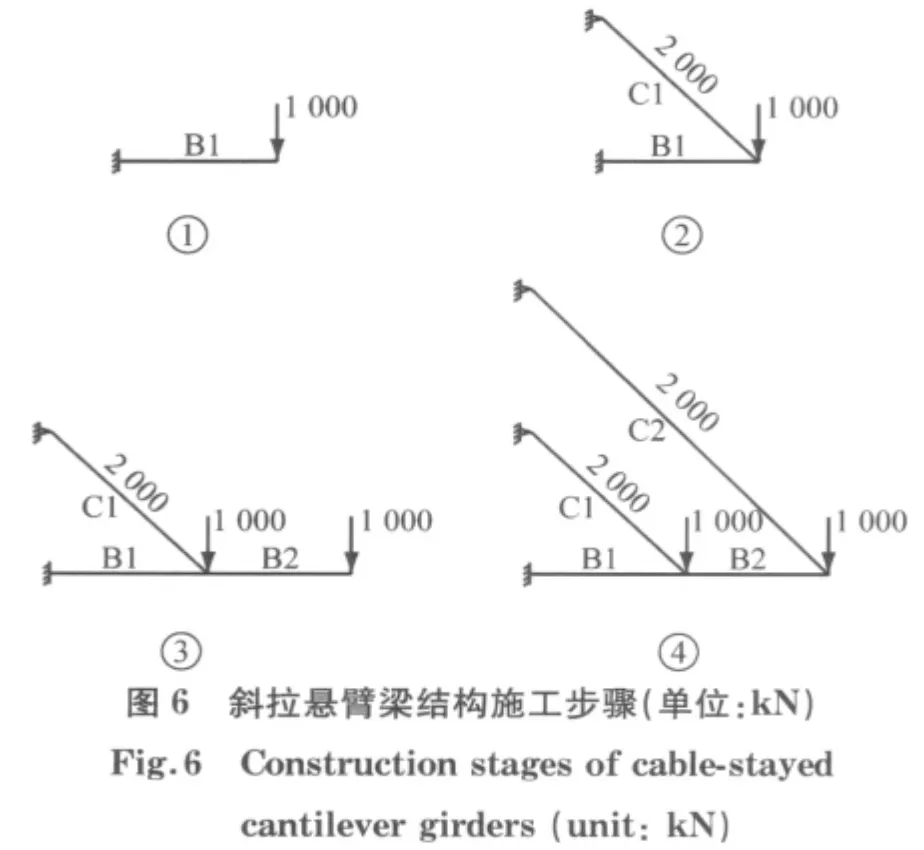
按平行安装进行施工过程分析，各施工步下节点1和节点2的竖向位移列于表1.从表中可看出，如果直接按模型位置进行构件安装，则安装完成后的节点1和节点2相对于建模位置向下分别偏移了217.5mm 和598.7mm，与设计线形相差很大，为消除这个位移，必须作施工控制分析.假设要求设计线形为图5所示的建模位置，即施工完成后梁段水平.按本文介绍的线形控制分析方法将节点坐标反拱，从表1中可看出，通过两次非线性迭代计算，节点1和节点2相对于建模位置的竖向位移均为0，达到设计线形.

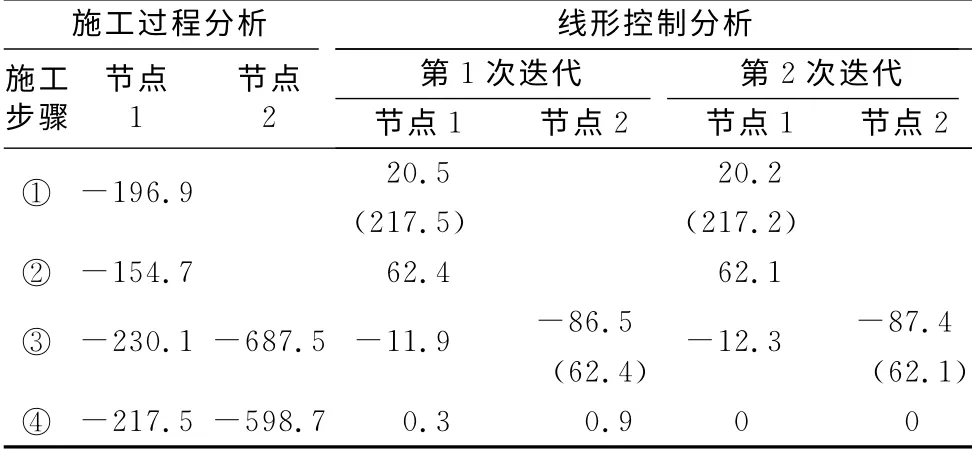
表1 节点竖向位移Tab.1 Vertical displacement of nodes mm

4.2 苏通大桥

苏通大桥为当今世界上跨径最大的斜拉桥（图7），其主跨径为1 088m；主梁为扁平钢箱梁，梁高4 m、宽41m，共分为17种类型、141个梁段，节段标准长度16m、边跨尾索区节段标准长度12m；斜拉索为7平行钢丝体系，全桥共设4×34对斜拉索，按扇形布置，空间索面；塔柱采用倒Y 型结构，高300.4m.

施工过程为：先施工边跨和索塔，梁段采用先简支后连续施工；然后双悬臂施工至10 号梁段，实现边跨合龙；再单悬臂施工至中跨34号梁段，实现中跨合龙.施工阶段数为256步.本文采用8段只拉桁架短索单元模拟1根长索，进行几何非线性施工过程和施工线形控制数值模拟分析，施工过程分析采用切线安装模型，施工线形控制分析采用建模位置安装模型.

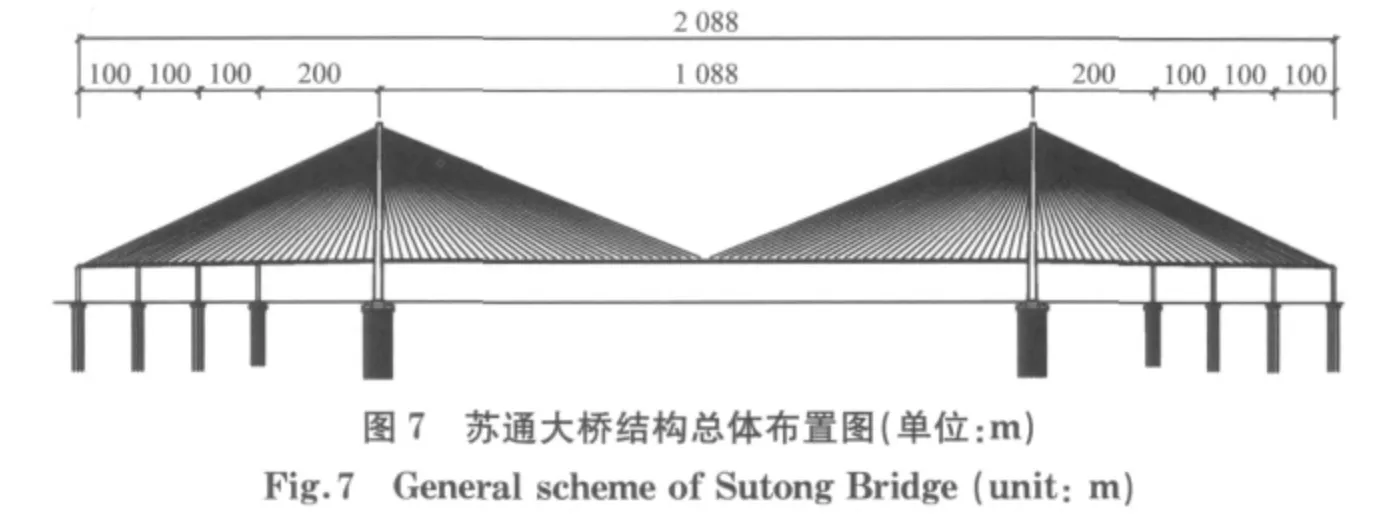
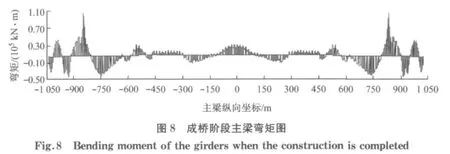
图8 为成桥阶段主梁弯矩图，最大正弯矩为1.042 3×105kN·m，最小负弯矩为－4.998 1×104kN·m.为了验证本文非线性施工过程分析方法的正确性，将计算结果与国际著名桥梁设计软件TDV 2000作了对比研究.表2列出了施工过程第100步、150步和成桥阶段主梁弯矩值.通过对全部256个施工阶段的对比分析，结果显示所有阶段主梁弯矩误差均在1%以内.从计算时间上看，用同一台计算机计算，TDV 运行整个施工过程需要56 min，而BINAS只需22min，由此可看出稀疏矩阵求解器具有很高的计算效率.

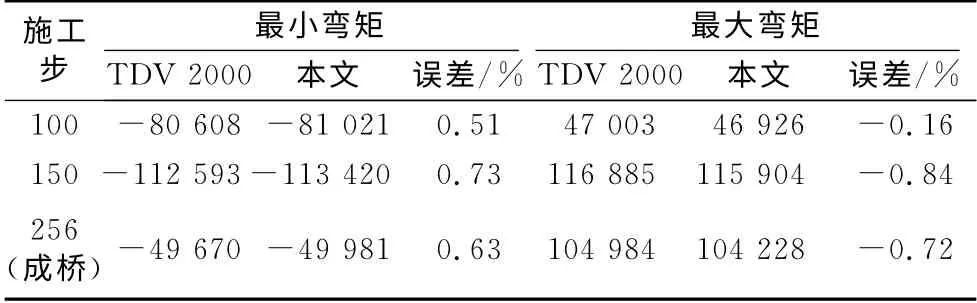
表2 施工阶段主梁弯矩Tab.2 Bending moment of the girders at construction stages kN·m

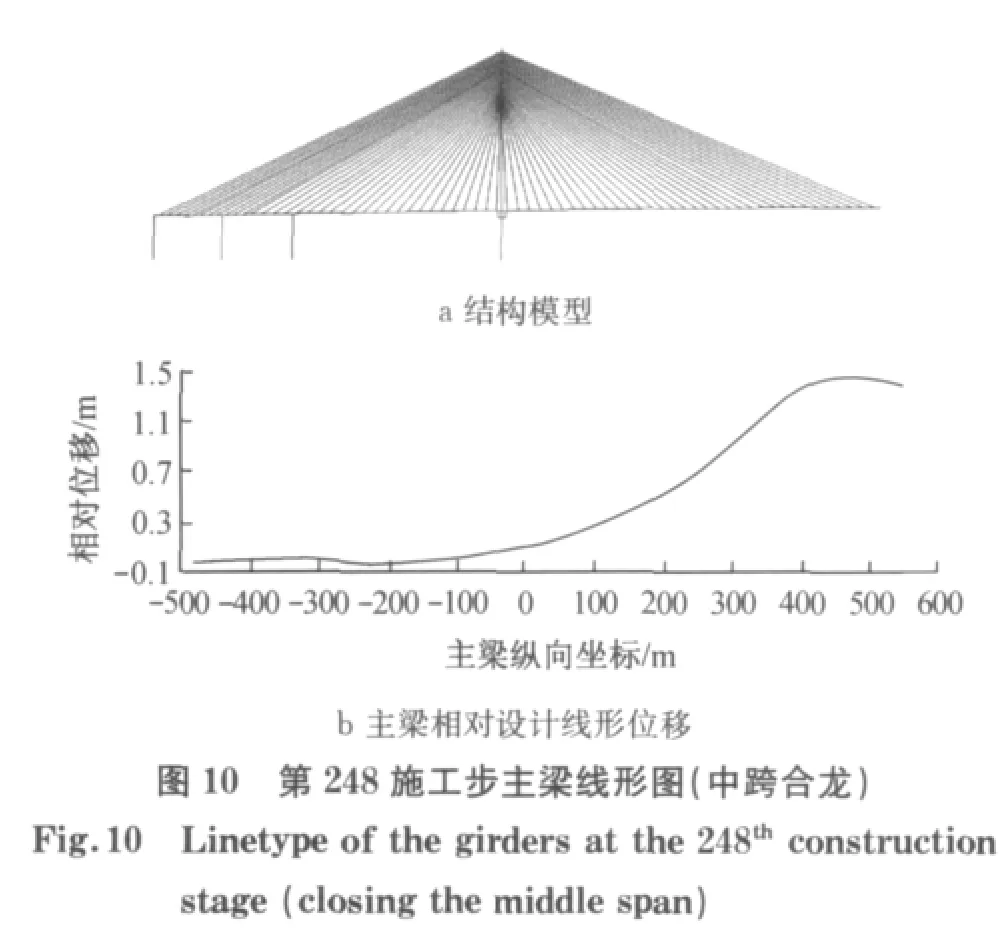
施工过程线形控制迭代计算结果显示：第1次迭代后主梁的线形与设计线形最大竖向误差为124 mm，第2次迭代后的误差为9.5mm，第3次迭代后的误差为0.8mm，满足精度要求；第100个施工步悬臂端最大偏移量为0.247m，第248个施工步主梁最大偏移量为1.430m.图9和图10分别显示了第100和248个施工步主梁相对设计线形位移图，考虑到模型几何和荷载的对称性，图形按结构的1／2 绘制.根据施工控制分析结果，可以方便地得到斜拉索的无应力长度和构件安装时的位置.

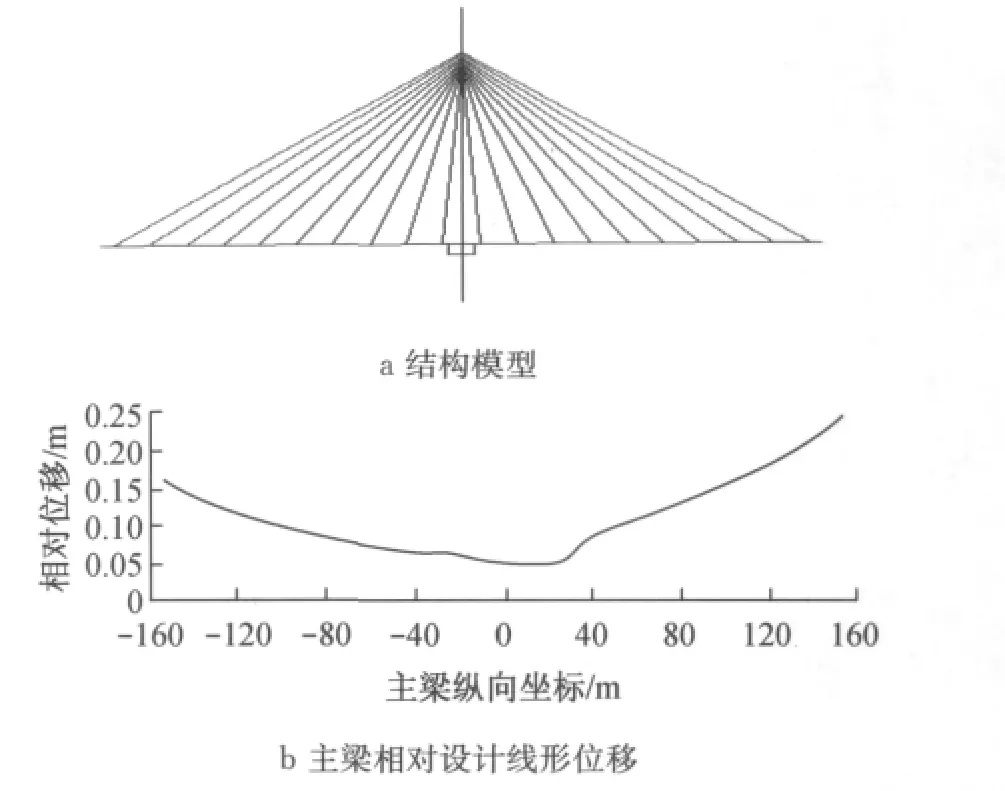
图9 第100施工步主梁线形图（吊机前移，第2次张拉10号索）Fig.9 Linetype of the girders at the 100th construction stage（moving the hoister and tension the 10th cable for the 2nd time）

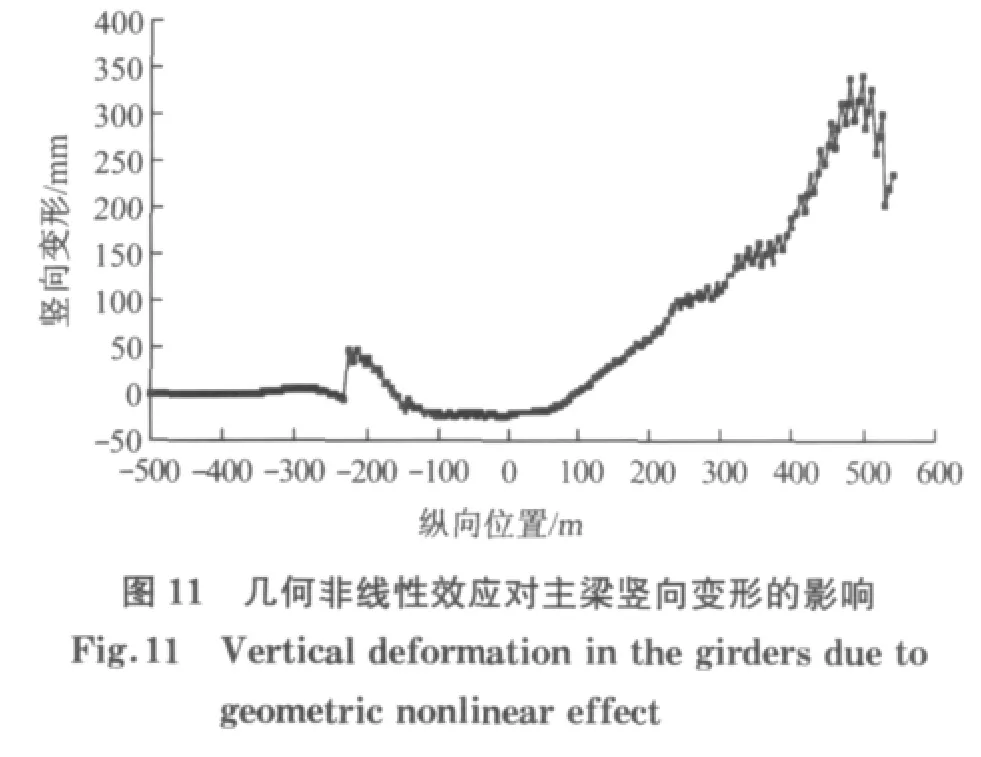
大跨度钢斜拉桥线形控制分析中的几何非线性效应如图11所示.对于中小跨度桥梁，将线形施工过程分析的成桥位移值反号叠加到设计线形上，即可得到满足设计要求的近似安装线形.基于近似安装线形，按建模位置模型进行几何非线性施工过程分析，苏通大桥主梁的最大偏离值约为350 mm，超出钢梁容许偏差L／10 000＝108.8mm，而按上述的非线性精确安装线形进行安装，成桥线形与设计线形最大偏差仅为0.8mm.因此，大跨度钢斜拉桥线形控制分析中必须考虑几何非线性的影响.

5 结论

（1）在几何非线性有限元的基础上，本文通过多段短索模拟斜拉长索的非线性效应，按照增量方法调整索无应力长度模拟施工过程索的多次张拉效应，算例表明该方法具有很好的精度和收敛性.

（2）本文提出了3种施工过程新增构件激活方式，即切线安装、平行安装和建模位置安装.其中切线安装和平行安装用于施工过程分析，模拟施工过程中新增构件的不同安装方式；建模位置安装用于线形控制分析，通过非线性迭代计算得到安装线形.

（3）大型稀疏矩阵求解器可大大节省计算机内存，提高运算速度，解决了多步非线性分析迭代计算费用的瓶颈问题.

（4）基于斜拉桥施工过程分析和控制理论编制的BINAS软件已成功地应用于苏通大桥的施工过程线形控制分析中，计算表明，大跨度钢斜拉桥线形控制分析中必须考虑几何非线性的影响.

［1］ WANG Paohsii，TANG Tzuyang，ZHENG Hounong.Analysis of cable－stayed bridges during construction by cantilever methods［J］.Computers and Structures，2004，82（4－5）：329.

［2］ 闫维明，张志，陈彦江，等.大跨度斜拉桥施工过程中的索力控制方法［J］.土木建筑与环境工程，2010，32（5）：130.YAN Weiming，ZHANG Zhi，CHEN Yanjiang，et al.Method of cable tension controlling in the long－span cable－stayed bridge construction ［J］. Journal of Civil， Architectural ＆Environmental Engineering.2010，32（5）：130.

［3］ 李熠，颜东煌，李学文.混凝土斜拉桥合理成桥状态研究［J］.重庆交通大学学报：自然科学版，2008，27（6）：1017.LI Yi，YAN Donghuang，LI Xuewen.Research on the reasonable finished dead state of concrete cablestayed bridges［J］.Journal of Chongqing Jiaotong University：Natural Science Edition.2008，27（6）：1017.

［4］ Pedro J J，Reis A J.Nonlinear analysis of composite steelconcrete cable－stayed bridges ［J］.Engineering Structures，2010，32（9）：2702.

［5］ Freire A M S，Negrão J H O.Geometrical nonlinearities on the static analysis of highly flexible steel cable－stayed bridges［J］.Computers and Structures，2006，84（31－32）：2128.

［6］ 李乔，卜一之，张清华.基于几何控制的全过程自适应施工控制系统研究［J］.土木工程学报，2009，42（7）：69.LI qiao，BU Yizhi，ZHANG Qinghua.Whole－procedure adaptive construction control system based on geometry control method［J］.China Civil Engineering Journal.2009，42（7）：69.

［7］ 张建民，肖汝诚.千米级斜拉桥施工过程中的索力优化与线形控制研究［J］.土木工程学报，2005，38（7）：54.ZHANG Jianmin，XIAO Rucheng.Cable force optimization and linetype control for the construction of a thousand meter scale cable－stayed bridge［J］.China Civil Engineering Journal.2005，38（7）：54.

［8］ 谭红霞，张建民.大跨度斜拉桥施工过程索力和线形双控研究［J］.河海大学学报：自然科学版，2008，36（1）：97.TAN Hongxia，ZHANG Jianmin.Cable prestress and alignment double control during construction of large－span cable－stayed bridges［J］.Journal of Hohai University：Natural Science Edition.2008，36（1）：97.

［9］ 吴国胜，袁保军.基于几何控制法的斜拉桥参数敏感性分析［J］.重庆交通大学学报：自然科学版，2008，27（6）：1020.WU Guosheng，YUAN Baojun.Analysis on sensitivity of parameters of cable－stayed bridge based on geometry control method［J］.Journal of Chongqing Jiaotong University：Natural Science Edition.2008，27（6）：1020.

［10］ 肖汝诚.桥梁结构分析及程序系统［M］.北京：人民交通出版社，2002.XIAO Rucheng.Analysis and program system for bridge structure［M］.Beijing：China Communications Press，2002.