单层网壳结构稳定性分析的随机缺陷模态迭加法

刘慧娟，罗永峰，杨绿峰，4，张 伟

（1.广西大学 土木建筑工程学院，广西 南宁530004；2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁530004；3.同济大学 土木工程学院，上海200092；4.广西壮族自治区住房和城乡建设厅，广西 南宁530028）

单层网壳结构的典型破坏形态为失稳破坏，其失稳模式和稳定承载力分析方法的研究十分重要.目前，基于非线性有限元理论的荷载—位移全过程分析法是研究网壳结构非线性平衡路径的主要分析方法.该方法的关键是平衡路径的跟踪求解，目前的主要方法包括人工弹簧法［1］、位移控制法［2］、弧长控制法［3］及自动增量求解技术［4］.初始缺陷对单层网壳结构的失稳模式和稳定承载力有显著影响［5］.对有初始缺陷网壳结构的稳定性分析，除基于连续化方法的拟壳法［6－7］外，应用较多的还有基于离散方法的解析法和数值计算法.在解析法研究方面，Koiter提出了缺陷敏感性分析的渐进理论，Tompson，Budiansky以及Hutchinson等发展了这一理论［8］.渐进法以分支点的微小邻域作为研究对象，难以直接应用于复杂结构［9］，因而数值计算方法开始发展起来，包括确定性方法和随机有限元方法.其中，忽略了缺陷随机性的确定性方法又包括优化方法［10］、临 界 缺 陷 模 态 法［11］、一 致 缺 陷 模 态 法（CRIMM）［12－13］及其改进方法.优化方法不具有通用性，即需针对具体问题进行求解.临界缺陷模态法认为非完善结构的平衡路径可看作完善结构在缺陷作用下发生的微小扰动，因而难以分析位移较大的复杂结构.一致缺陷模态法认为最低阶屈曲模态是结构屈曲时的位移倾向，与结构屈曲模态相同的初始缺陷对结构产生不利影响，但是，目前尚没有相关研究成果或理论可以证明此说法，最低阶屈曲模态也可能不是最不利缺陷模态.关于初始缺陷随机性的研究相对较晚.赵惠麟等［14］运用Monte Carlo法对随机稳定承载力进行了研究，假设结构的初始缺陷服从正态分布，得到承载力的特征值，进而得到统计意义上的结构稳定承载力.黄斌等［15］采用随机缺陷模态法（SIMM）考虑节点缺陷的随机性，计算结果精度较高，但对多自由度复杂结构，随机变量为3倍节点个数，样本计算量大.文献［15］指出缺陷模态可看作是若干屈曲模态的耦合，对基于某一阶屈曲模态的缺陷网壳结构进行一致缺陷模态分析，定性得出缺陷的前4阶屈曲模态耦合系数，并未对缺陷模态耦合的随机性进行理论论证及数值分析.现有渐进法只适用于简单结构，难以应用在复杂工程中.而确定性方法由于忽略了缺陷的随机性，难以得出准确的结果，随机缺陷模态法及改进方法通常是基于Monte Carlo方法，样本计算量较大，工程应用受限.

为此，本文在线性屈曲分析的基础上，通过建立结构缺陷模态参与系数的概率模型，提出基于Timeshenko梁理论的网壳结构稳定性随机缺陷模态迭加法（SIMSM），采用Monte Carlo法对具有随机缺陷的结构进行稳定承载力分析，弥补了随机缺陷法及改进随机缺陷法［14］样本计算量大的缺点，给出设计临界荷载的可靠性问题，并进行了算例验证.

1 有缺陷网壳结构稳定性分析方程

离散化分析法包括半解析半离散和梁 柱单元理论［6，16］，以及应用较多的非线性有限元理论.结合几何非线性有限元理论及基于非线性有限元理论的Timeshenko梁单元的基本假定［17］，推导建立该形式空间梁的切向刚度矩阵方程.

Timeshenko梁单元总势能为

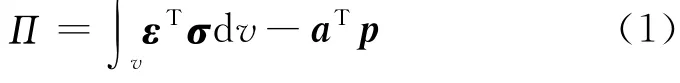
式中，ε，σ，a，p分别为单元的应变向量、应力向量、位移向量以及等效节点荷载向量.

式（1）中梁单元总线应变向量为

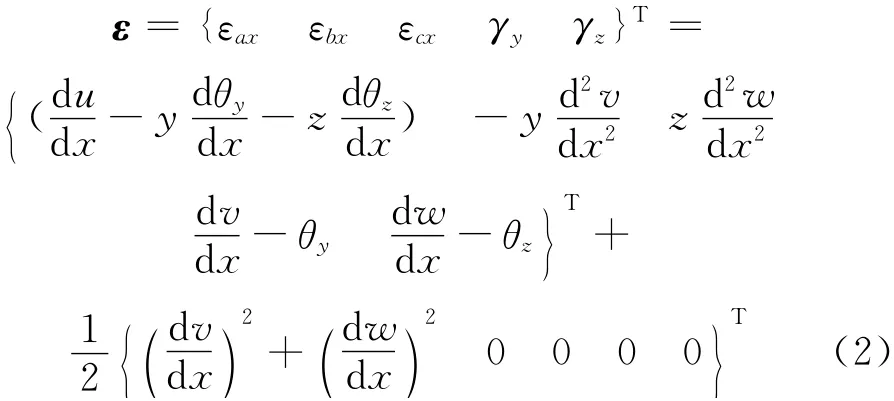
式中：εax，εbx，εcx分别为位移（u，v，w）1阶导数所产生的轴向应变所 产生 的 轴 向 应 变；γy为y向剪应变；θy为x，y平面内绕y轴的横截面转角；γz为z向剪应变；θz为x，z平面内绕z轴的横截面转角.

考虑δΠ＝0，以及δε＝Bδa和σ＝Dε，其中，B为应变矩阵，D为弹性模量矩阵，则式（1）可变为网壳结构非线性变分形式

根据变分和增量的特性，可将变分形式的式（3）写成增量的形式

式中：Δa为位移增量向量.此时增量平衡方程（4）变为

式中：Q为结构节点荷载向量；F为本增量步初始结构内力向量.

采用Newton－Raphson 方法结合柱面弧长法，可求解方程（5），并可跟踪每个荷载增量下节点位移的增量，获得结构在整个荷载加载过程中的屈曲路径.

2 稳定分析的随机缺陷模态迭加法

首先，根据结构刚度矩阵K，求解线性屈曲的特征值λi（i＝1，2，…，m）和相应的屈曲模态Ui，其中m是参与组合的模态阶数.由于节点位置缺陷具有随机性，需考虑缺陷模式ΔX的随机性.为此，假定任一缺陷模式为

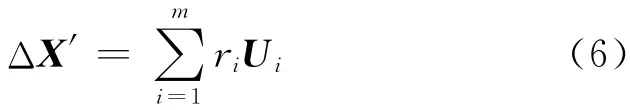
式中：m为模态参与阶数；r1，r2，…，rm为参与系数，是服从均匀分布的独立随机变量，取值范围为［－1，1］；Ui为结构第i阶线性屈曲模态，且满足

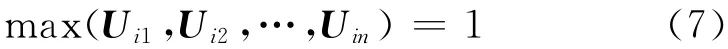
式中：n为结构节点数；Uin为第i阶屈曲模态中第n个节点的位移向量.

对ΔX′进行幅值调整，以获得幅值为R的缺陷模式向量ΔX

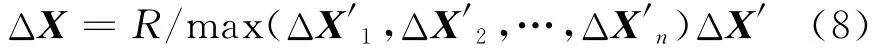
式中，ΔX′1为ΔX′中的节点1 的位移向量.根据式（8）可得有缺陷结构的节点坐标向量

由于ΔX为随机变量ri的函数，则随机有限元刚度方程形式同方程（5）.

利用Monte Carlo随机抽样法，基于确定性非线性有限元分析求解随机有限元方程式（5）.建立随机向量r的概率模型f（r：φ），其中φ为参数向量.按照f（r：φ）的特点，进行第1次随机抽样，生成一组随机参与系数，即r（1），则此时

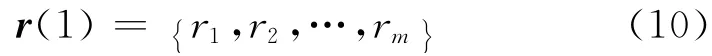
式中，r（）的括弧内数值表示抽样次数，假定总抽样次数为t.

将式（10）中的ri代入式（6），并根据式（7）—（9）计算出有缺陷结构的节点坐标向量X.根据X，更新结构数学模型，进而更新随机有限元方程（5），然后通过求解该方程，获取结构在整个加载历史过程中每个增量步的结构切线刚度矩阵KT，计算

式（11）第1次成立时，即结构第1次达到临界状态，获取外荷载因子q和结构屈曲模态构型Us1.此时，则结构临界荷载因子λcl的第1次抽样值为

结构的临界变形Ucr为

重复抽样和上述计算过程t后，可得到数组λcl（i）（i＝1，2，…，t），利用数理统计方法计算该数组的数学期望μ和均方差σ.通过假设检验，确定结构临界荷载分布形式.

经验证，本文算例中临界荷载分布成正态分布.由于单层网壳对缺陷非常敏感，因而可采用数理统计3σ原则确定最低临界荷载因子λ为

3 算例分析

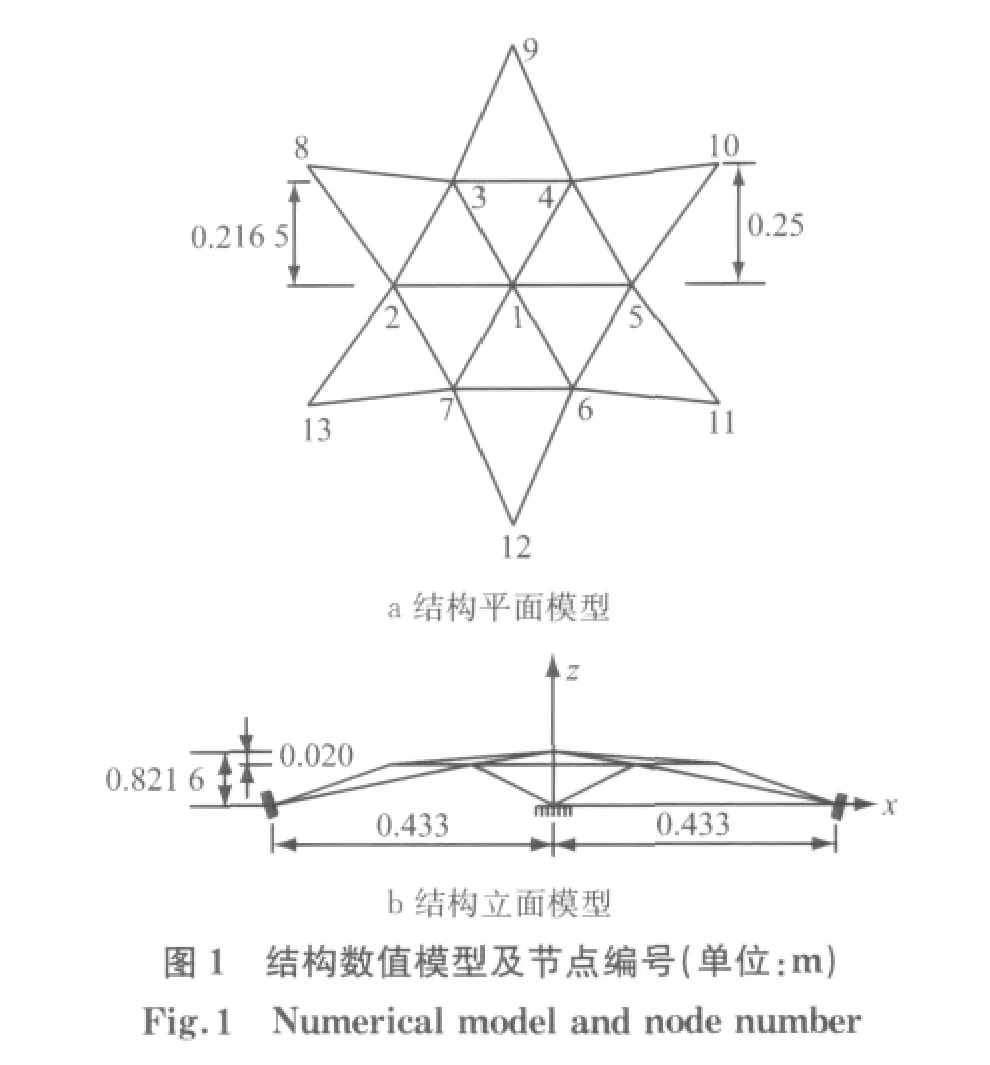
对图1 所示的6 角扁网壳结构［16］进行算例分析.杆件离散为Timeshenko 梁单元，其截面积为317mm2.周边为3向固定铰支座.材料弹性模量为3 030 MPa，剪切模量为1.096×103MPa.荷载P向下作用在顶点处.计算过程采用Ansys有限元软件的APDL 语言编程实现，其中网壳杆件采用Beam188，该单元为2 节点Timeshenko梁单元，挠度、转角的独立插值函数为C0型；非线性计算过程采用弧长法稳定数值计算，利用残余力的2 范数作为收敛准则.

3.1 理想无缺陷结构稳定性分析

理想无缺陷结构的前10阶线性屈曲系数如表1所示.由该表可知，前3阶屈曲系数比较接近，最低阶屈曲系数即临界荷载因子为2.565.结构的最低阶屈曲模态U1如图2所示，由该图可知，第1阶屈曲模态为顶点上凸和周边节点3—7下凹的失稳模式.

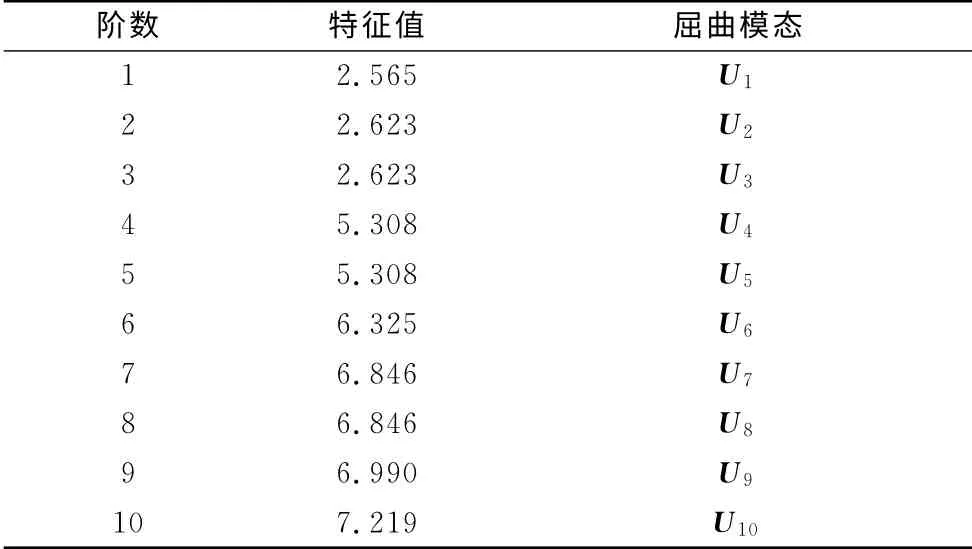
表1 网壳结构的线性屈曲系数和屈曲模态Tab.1 Buckling factors and corresponding modes of the lattice dome

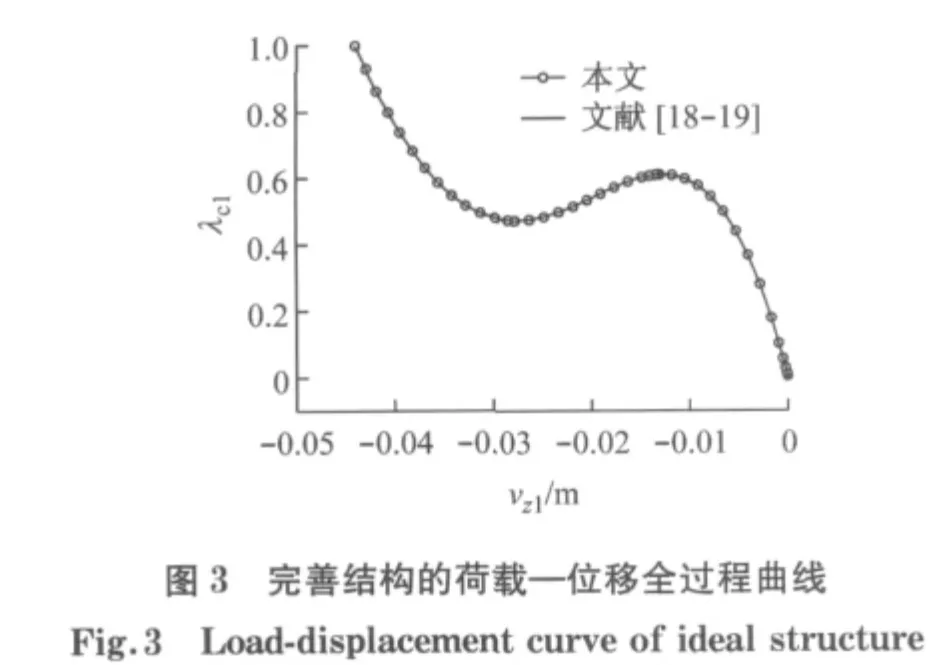
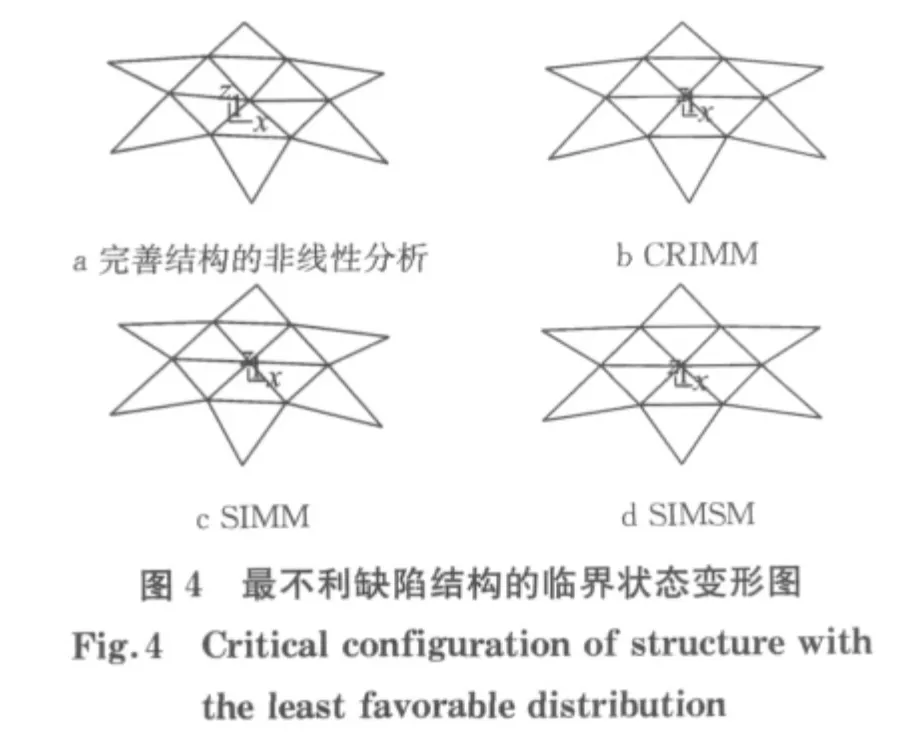
对理想结构进行荷载—位移全过程非线性分析，节点1的荷载—位移全过程曲线如图3所示，采用vz1表征节点1的竖向位移.从图中可知，结构非线性临界荷载因子为0.615，临界状态变形如图4a所示.由该图可知，结构的失稳模态为顶点下凹引起的轴对称失稳模式.本文采用荷载—位移全过程分析出的临界荷载计算值和失稳模式与J.L.Meek［18－19］采用同样方法的计算结果非常吻合，验证了本文模型和荷载—位移全过程方法的正确性.

3.2 随机初始缺陷分析

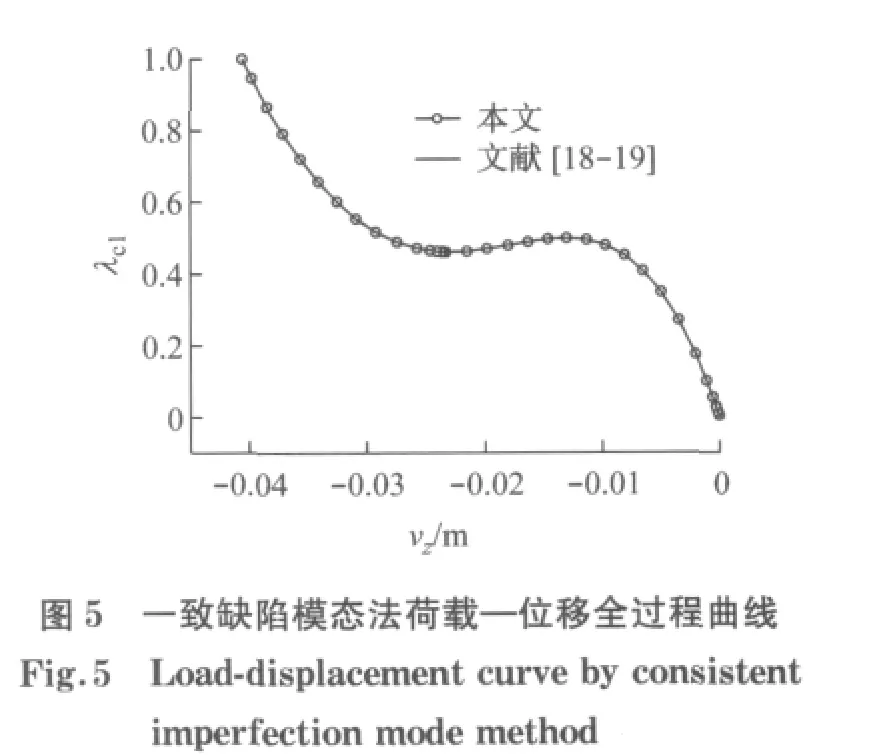
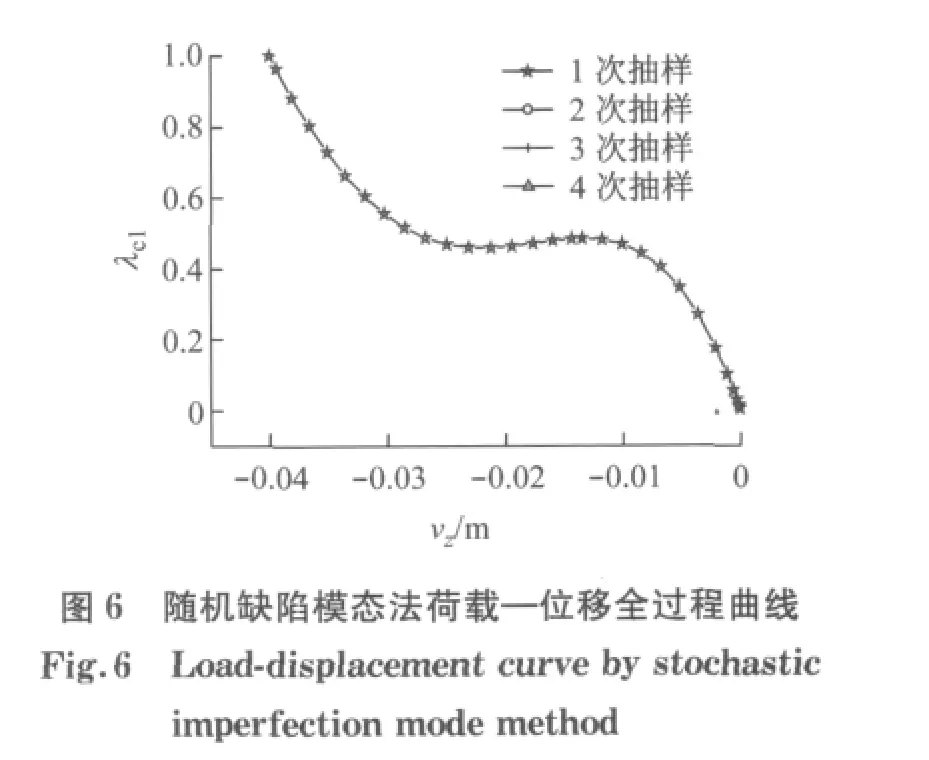
为了更好地考察SIMSM 方法的性能，首先采用传统方法CRIMM 和SIMM（抽样1 000 次），考虑0.002m 的初始缺陷，分别对图1 所示的算例进行分析.根据图5 给出的CRIMM 得到的结构荷载—位移全过程曲线，利用式（12），可判断出其非线性临界荷载因子为0.500，按照式（13）可获得如图4b所示的结构临界变形，由该图可知结构的失稳模态为顶点下凹、周边节点3—7上凸的模式.采用SIMM，随机抽样1 000次，得到图6所示的最不利缺陷分布下的荷载—位移全过程曲线，最小非线性临界荷载因子为0.485 5，利用式（14）计算出最低非线性临界荷载因子为0.454 3，按照式（13）可获得如图4c所示结构临界变形，由该图知，结构的临界失稳状态呈现出顶点下凹而导致结构整体失稳的特征.

下面采用SIMSM 方法对该缺陷结构进行分析.表1所示前3阶线性屈曲系数较小，且很接近，根据SIMSM 原理，认为结构最不利缺陷模式主要由U1，U2，U3齐次组合而成的，其参 与系数r1，r2，r3为独立随机变量.根据式（7）和式（8）可得到结构缺陷分布模式ΔX，利用式（5）将ΔX引入结构.采用Monte Carlo方法抽样1 000次，对每一次抽样进行荷载—位移全过程分析.

前4次抽样所获得的结构荷载—位移曲线如图7所示.由该图可知，结构失稳模式为点失稳，具有跳跃失稳的特征［20］.结构最不利缺陷分布下的结构荷载—位移曲线如图8所示，其中最小非线性临界荷载因子为0.436 3，此时结构的前3阶参与系数的比例为－4.0∶－1.0∶1.5.结构的临界失稳状态呈现出顶点下凹的整体失稳的特征，如图4d所示.利用式（12）可确定结构临界荷载因子λcl＝0.328 8，其概率可靠度为99.70%.

前述各方法计算的最低非线性临界荷载因子如图9所示.由图可知，SIMSM 的临界荷载因子比完善结构的非线性临界荷载因子降低46.54%，比CRIMM 的计算值降低34.24%，比SIMM 所得的数值小27.63%.因此，SIMSM 的临界荷载因子最小，可靠度最高（为90.07%）.因此，SIMSM 临界荷载更为不利.对于实际工程应用，采用SIMSM指导结构设计，更有利于安全、可靠的网壳结构的建造.

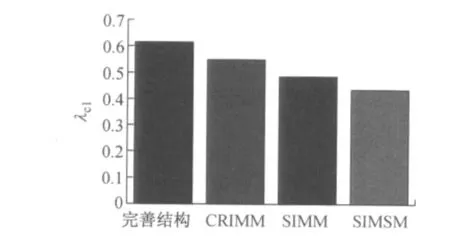
图9 最不利缺陷结构的临界荷载因子Fig.9 Critical buckling load factor under the least favorable distribution

4 最不利参与组合模态数

从计算精度方面看，参与的组合模态数越多，最终计算的最低阶临界荷载值越精确；实际上，这将直接导致随机量增大，且需要增加抽样次数保证精度，计算量将大幅增加.因此，需要在计算精度和计算成本之间寻找一个平衡点，即寻找到同样抽样次数下，最不利参与组合模态数.

从表2 和图10 可以看出，同一参与组合模态下，抽样的次数越多，求解的屈曲荷载因子最低，求解越精确；在固定抽样次数下，不同模态参与组合，计算值稍有变化，其中由前2个模态参与的组合所求的屈曲荷载因子最低，对应的临界荷载因子为0.432 3，即为最不利临界荷载因子λcl.

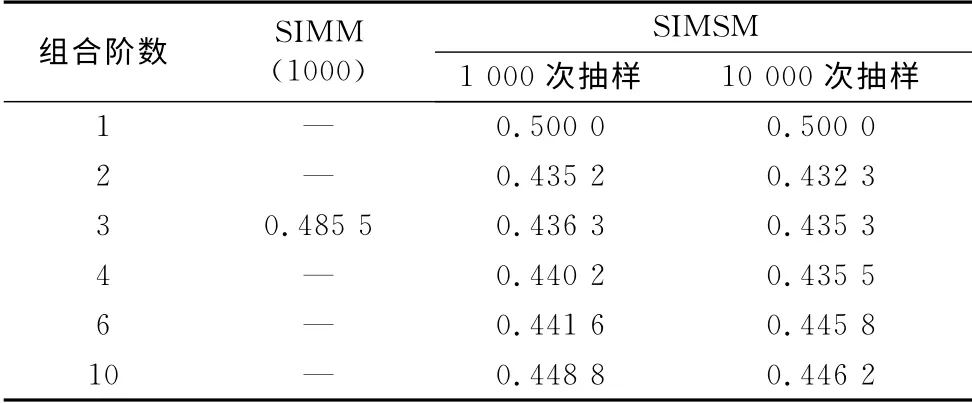
表2 网壳结构的最低临界屈曲荷载因子Tab.2 Critical buckling load factor of the lattice dome

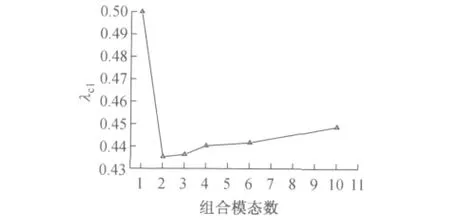
图10 参与组合的模态数Fig.10 Combinatorial mode number

5 结论

基于Timeshenko梁理论，结合随机缺陷理论，建立了网壳结构稳定性分析的随机缺陷模态迭加法.采用随机缺陷模态迭加法对6角扁网壳结构进行了算例分析，并与线性屈曲分析、一致缺陷模态法和随机缺陷模态法的非线性计算结果进行对比，计算结果表明：①采用随机缺陷模态迭加法寻找的最不利临界荷载最低，而线性屈曲分析法、一致缺陷模态法和随机缺陷模态法计算出的最低临界荷载均有更高的失效概率；②最不利缺陷模态的参与系数比例为4.0∶－1.0∶1.5，可见最低阶模态参与系数较高，较低阶参与系数较低，且有可能是模态反向参与；③在固定抽样次数下，选择不同的参与模态数，会影响不利屈曲荷载因子的计算值大小；本算例最不利参与组合的模态是前2阶；④研究发现，最不利屈曲临界荷载下，结构呈现顶点下凹的点失稳的特征.因此，算例分析表明，随机模态迭加法可求解结构最不利缺陷临界荷载和失稳模式，且验证了该法的正确性和可行性，可为工程应用提供较准确安全的设计荷载，并具有一定的普适性.

［1］ Sharifi P，Popov E P.Nonlinear buckling analysis of sandwich arches［J］.Journal of Engineering Mechanics Division，1971；97（5）：1397.

［2］ THAI Huutai，KIM Seungeock.Large deflection inelastic analysis of space trusses using generalized displacement control method［J］.Journal of Constructional Steel Research，2009；65（10－11）：1987.

［3］ Lee Kyoungsoo，Han Sangeul，Park Taehyo.A simple explicit arc－length method using the dynamic relaxation method with kinetic damping［J］.Computers ＆Structures，2011；89（1－2）：216.

［4］ Bathem K J，Dvorkin D N.On the automatic solution of nonlinear finite element equations ［J］. Computers ＆Structures，1983，17（5／6）：871.

［5］ THAI Huutai，KIM Seungeock.Nonlinearinelastic analysis of space frames［J］.Journal of Constructional Steel Research，2011；67：585.

［6］ 董石麟，詹伟东.单双层球面扁网壳连续化方法非线性稳定理论临界荷载的确定［J］.工程力学，2004，21（3）：6.DONG Shilin，ZHAN Weidong.Non－linear stability critical loads of single－layer and double－layer reticulated spherical shallow shells based on continuum analyogy method［J］.Engineering Mechanics，2004；21（3）：6.

［7］ Limam Ali，El Bahaoui Jalal，Khamlichi Abdellatif，et al.Effect of multiple localized geometric imperfections on stability of thin axisymmetric cylindrical shells under axial compression［J］.International Journal of Solids and Structures，2011，48（6）：1034.

［8］ Kiyohiro Okeda，Makoto Ohsaki.Generalized sensitivity and probability and analysis of bucking loads of structures［J］.International Journal of Non－linear Mechanics，2007；42（5）：733.

［9］ 黄宝宗，任文敏.Koiter稳定理论及其应用［J］.力学进展，1987，17（1）：30.HUANG Zongbao，REN Wenmin.Koiter stability theory and application［J］.Advances in Mechanics 1987；17（1）：30.

［10］ Makoto Ohsaki，Kiyohiro Ikeda.Stability and optimization of structures－generalized sensitivity analysis ［J］. Springer Science Business Media，2007，47－50：183.

［11］ 敖鸿斐.临界缺陷模态法在网壳缺陷敏感性分析中的应用［D］.上海：同济大学土木工程学院，2005.AO Hongfei.Application of the method of critical imperfection modes to the analysis of imperfection sensitivity of reticulated shells［D］.Shanghai：College of Civil Engineering of Tongji University，2005.

［12］ FAN Feng，CAO Zhenggang，SHEN Shizhao.Elasto－plastic stability of single－layer reticulated shells［J］.Thin－walled Structures，2010；48（10－11）：827.

［13］ 李元齐，沈祖炎.大跨度拱支网壳结构体系及静力性能研究［J］.浙江大学学报，2001，35（6）：645.LI Yuanqi，SHENG Zuyan.Arch－supported reticulated shell structures and their mechanical behaviors［J］.Journal of Zhejiang University.2001；35（6）：645.

［14］ 唐敢，赵惠麟，赵才其，等.板片空间结构缺陷稳定分析及试验研究［J］.土木工程学报，2008，41（8）：15.TANG Gan，ZHAO Huilin，ZHAO Caiqi.Theoretical and experimental study on the stability of sheet space structures with imperfections［J］.China Civil Engineering Journal，2008；41（8）：15.

［15］ 罗昱.改进的一致缺陷模态法在单层网壳稳定分析中的应用研究［D］.天津：天津大学建筑工程学院，2007.LUO Yi.Application improved consistent imperfection mode in buckling analysis on single－layer lattice dome［D］.Tianjin：College of Civil Engineering of Tianjin University，2007.

［16］ Oran C.Tangent stiffness in space frames［J］.ASCE，1973；99（6）：987.

［17］ 王勖成，劭敏.有限单元法基本原理和数值方法［M］.北京：清华大学出版社，1996.WANG Xucheng，SHAO Min.Finite element method ［M］.Beijing：Tsinghua University Press，1996.

［18］ 罗永峰.网壳结构弹塑性稳定及承载力全过程研究［D］.上海：同济大学土木工程学院，1991.LUO Yongfeng.Analysis on elastic－plastic stability and load bearing capacity for lattice domes［D］.Shanghai：College of Civil Engineering of Tongji University，1991.

［19］ Meek J L，Tan H S，Geometrically nonlinear analysis of spaceframes by an incremental iterative technique［J］.Computer Methods in Applied Mechanics and Engineering，1984；47：261－282.

［20］ CHEN Jensan，LI Yuontai.Effects of elastic foundation on the snap－through buckling of a shallow arch under a moving point load［J］.International Journal of Solids and Structures，2006；43（14－15）：4220.