土体边界面模型在ABAQUS软件中的研发与验证

钦亚洲，孙 钧

（1.同济大学 岩土及地下工程教育部重点实验室，上海200092；2.南通大学 交通学院，江苏 南通226019；3.杭州丰强土建工程研究院，浙江 杭州310006）

天然土体一般都存在明显的各向异性.Casagrande［1］认为土体各向异性可分为固有各向异性和应力诱发各向异性.前者是指土颗粒在沉积过程中，颗粒长轴总存在垂直于最大主应力排列的趋势；而后者则由于应力作用后土体变形而产生.一般的方法是将土体各向异性分为初始各向异性和应力诱发各向异性，而初始各向异性包含了固有各向异性和由于偏压固结产生的诱发各向异性两个部分.对各向异性的定量描述也存在两种方法，一种是基于微观结构，采用描述土颗粒空间排列特征的组构张量［2－3］；另一种是由宏观不等向固结现象，采用描述宏观土体各向异性特性的各向异性张量［4］，这两者之间可以相互转换.

各向异性会对土体剪切强度、应力应变行为，以及屈服面倾向等产生影响.一些研究结果表明，对于正常固结土，考虑土体各向异性后，其力学行为将趋于超固结土.

目前有多种能反映土体各向异性的本构模型，它们间的区别在于屈服面选择、采用的硬化形式等方面.多屈服面本构模型一般采用运动硬化来反映各向异性，单屈服面本构模型则一般采用旋转硬化来反映.

Wheeler［5］针对芬兰黏土，提出了一个能考虑土体初始各向异性及应力诱发各向异性的弹塑性本构模型：S－CLAY1.此前的各向异性模型都采用塑性体应变εpv作为各向异性张量αij的硬化因子，而SCLAY1模型则同时采用塑性体应变εpv及塑性偏应变εps作为旋转硬化因子，综合考虑两种塑性变形对各向异性张量的作用，所以更为合理.

在S－CLAY1模型的基础上，本文通过引入边界面理论，在S－CLAY1模型的基础上将其拓展为能同时模拟正常固结土和中等超固结土的本构模型，在ABAQUS软件中编程开发实现，并对所建议模型进行了模拟验证.

1 模型构建

弹塑性模型可以通过引入边界面理论，从而改造为一个边界面模型，分述如下.

1.1 边界面方程

在3维应力空间，边界面方程表达式如下：

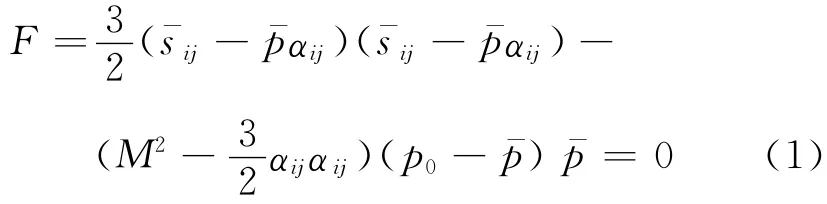
1.2 硬化法则

硬化法则包括两个部分：等向硬化法则和旋转硬化法则.

等向硬化法则由前期固结压力p0演化来反映，与修正的剑桥模型一致，以塑性体应变εpv作为硬化因子

式中：λ为e—lnp空间正常固结线的斜率；κ为e—lnp空间回弹曲线的斜率；v0＝1＋e0；e0为初始孔隙比.

各向异性张量αij的硬化法则为旋转硬化法则，以塑性体应变εpv及塑性偏应变εps作为硬化因子

式中：μ，β为常量参数，μ控制αij变化量的大小，β为控制塑性体应变率与塑性偏应变率对αij变化影响比例的因子；〈〉为Macaulay符号，含义为当时，当时为塑性偏应变分量增量.

Wheeler给出了参数μ，β的确定方法和范围.根据Wheeler的建议，μ一般取10／λ～15／λ，β／M取值在0.5～1.0.

1.3 映射法则

采用径向映射法则［6－7］，如图1所示.

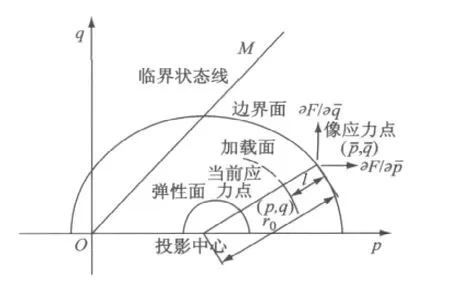
图1 边界面及径向映射示意图Fig.1 Schematic illustration of bounding surface and mapping rule

径向映射为从投影中心引出直线，经过当前应力点（p，q），与边界面交于点，此点定义为当前应力点的像点.

图1中，l为当前应力点与像点之间的距离，r0为投影中心到像点之间的距离，定义比例因子b为

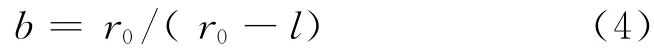
式中b必须满足b≥1.

则像点处应力与当前应力存在有以下关系：

1.4 塑性模量

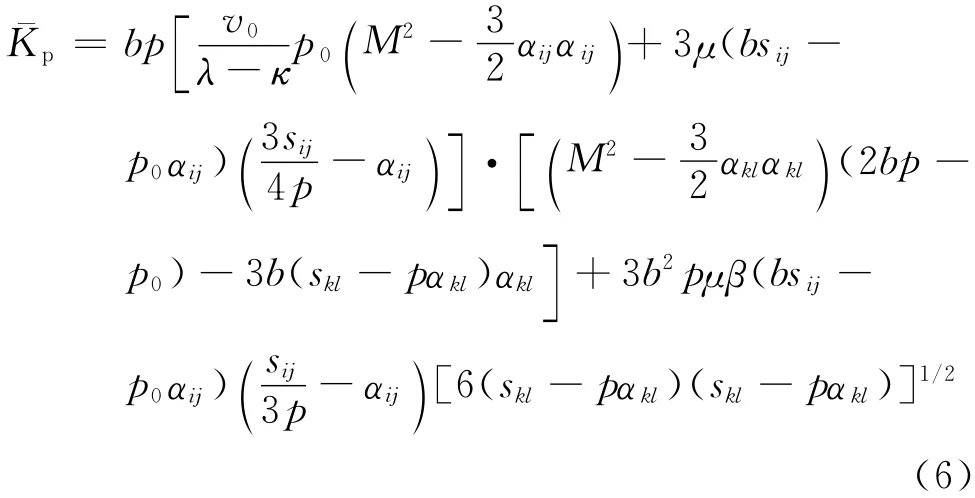
当前应力点的塑性模量Kp可由及当前应力点至投影中心距离插值求出.Kp插值函数的选择，影响模型的准确性.

本模型插值函数表达式为

式中：pa代表一个大气压，取100kPa；Rij为塑性流动方向；h代表加载纯弹性域的大小.对于黏土而言，几乎不存在一个加载纯弹性域，所以取h＝0；W为常量参数，一般可取W＝2.0.

2 数值计算

2.1 弹性应力应变关系

弹性应力应变关系与修正剑桥模型一致，为

式中：K为体积模量，随球应力变化；e·eij为弹性偏应变增量.

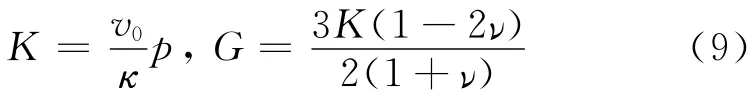
式中：G为剪切模量；ν为泊松比.

2.2 塑性应力更新算法

塑性应力更新算法采用图形返回算法，这是一种完全隐式积分算法，无条件稳定.它强化在时间步结束时的一致性，即fn＋1＝0，避免应力点离开屈服面而漂移，被证明是强健的和精确的［8］.算法示意图如图2.

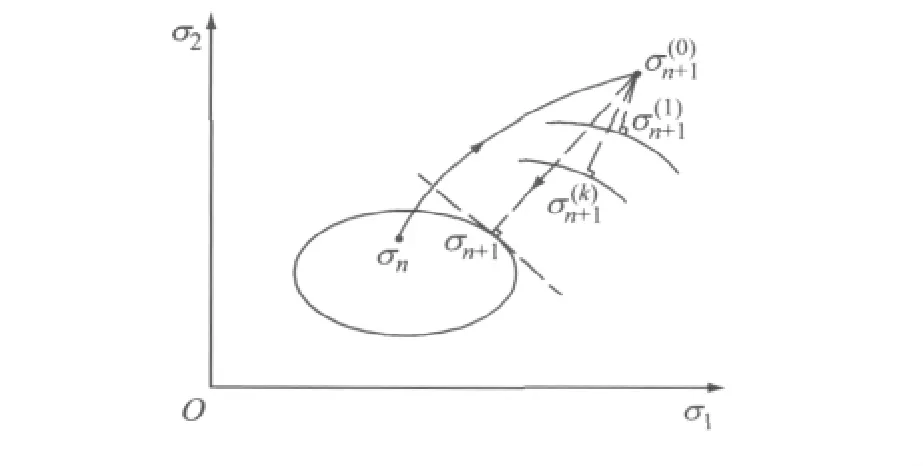
图2 图形返回算法示意图Fig.2 Schematic illustration of return mapping algorithm

算法分两步，第一步为弹性预测，第二步为塑性修正.

在弹性预测阶段，首先假定第n＋1步应变增量全部为弹性增量，得到弹性试探应力Δε，带入边界面方程中判断：若F＜0，只发生弹性变形，直接更新应力；若F≥0，则发生塑性变形，此时应力点可能位于屈服面之外，需要对应变增量、内变量、塑性加载因子等进行迭代修正，使得应力点沿塑性流动方向逐步拉回至新的屈服面，这个过程如图2所示.

Manzari［9］和费康［10］等采用隐式算法实现了对各向同性边界面模型的研发.

3 模型验证

借助于大型商业软件ABAQUS 所提供的UMAT（user－defined material）子程序接口完成了模型开发，编程时注意以下几点：

①ABAQUS中以拉应力为正；

②ABAQUS中剪应变为工程剪应变；

③ABAQUS中应力应变分量的顺序为σ11，σ22，

Stipho［11］及Ling［12］对高岭土进行了一系列三轴不排水剪切试验，可用来验证本模型.此次验证模拟了k0＝0.8的初始偏压固结情况，选用OCR＝1的正常固结土和OCR＝4的超固结土试样.模拟采用位移加载，直至轴向应变量达17%后停止加载.

3.1 模型参数选取

对于修正剑桥模型参数λ，κ，ν，M，p0按Stipho试验值选取；若土体处于k0正常固结状态，参数β可由下式确定：

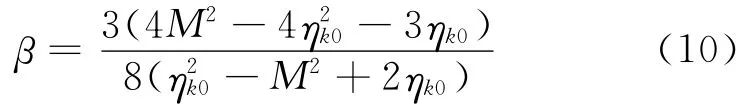
式中，ηk0为土体k0状态时应力比

因此取β＝0.6；参数μ的选取，Wheeler只给出大致取值区间.文献［13－14］给出一种确定参数μ的方法，若对k0正常固结土样施加大小为2～3 倍前期固结压力的等向围压后，土体宏观各向异性基本消失，从而由下式确定参数μ：

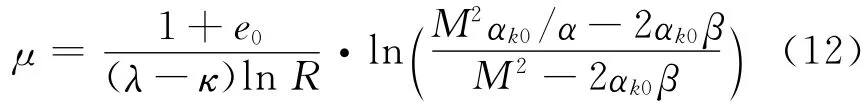
式中，αk0为土体正常k0状态时各向异性量，且

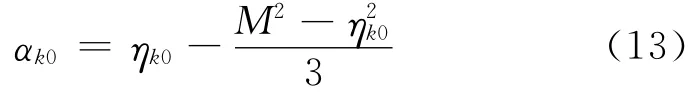
此外，在模型其他参数已确定的情况下，也可采用拟合试验数据方法确定参数μ的值.本文模型参数选取见表1.

表1 高岭土模型参数Tab.1 Model parameters for Kaolin clay

Wheeler文中已给出参数β随α／M，η／M的变化规律，所以本文只考察参数μ对土体工程行为的影响.在保持其他参数取值不变的情况下，分别取μ＝0，15，30，60对OCR＝1，k0＝0.8的初始偏压固结土不排水剪切试验进行了模拟，结果如图3和图4.

由图3和图4可见，随着μ值的增大，土体的剪切强度增大，并且在剪切过程中，土体应力路径外扩，这都反映了旋转硬化的影响.

3.2 试验模拟结果

若将本模型参数μ设置为零，则模型退化为各向同性边界面模型.本文分别采用各向同性边界面模型和各向异性边界面模型对试验进行了模拟，模拟结果如图5，6，7所示.

由模拟结果可见，总体上各向异性模型模拟的结果与试验值较吻合.根据土体临界状态理论，当土体应力状态到达破坏线（M线）时，此时土体塑性体应变εpv不再发生变化，也就是土体不再发生等向硬化.所以各向同性模型在达到临界状态后，强度曲线会出现水平段，如图5虚线所示.这使得各向同性模型低估了土的抗剪强度，并使得孔压也与试验值存在些偏差.各向异性模型由于采用了包含塑性剪应变εps的旋转硬化法则，所以当土体应力达到临界状态后，由于εps的存在，土体仍然会发生旋转硬化，强度曲线表现为沿M线继续向上一小段，如图6实线所示.

对于超固结土的不排水剪切试验的模拟，两种模型都存在一些偏差.

4 结论

在Wheeler弹塑性模型的基础上，结合边界面理论，将弹塑性模型拓展为各向异性边界面模型.模型采用旋转硬化法则来反映土体的初始各向异性及随后的应力诱发各向异性.利用软件ABAQUS提供的UMAT 子程序接口，采用隐式积分算法——图形返回算法编程实现.通过对k0＝0.8的初始偏压固结土体三轴不排水剪切试验的模拟，并与试验结果验证表明，模型能够合理描述正常固结土及中等超固结土的应力应变行为、孔压曲线及应力路径等.此外，相比于其他各向异性模型，本模型参数量少，除修正剑桥模型参数外，只另增加3个参数，且参数易于确定.

［1］ Casagrande A，Carrillo N.Shear failure of anisotropic materials［J］.Journal of Boston Society of Civil Engineers，1944，31（4）：74.

［2］ Anandarajah A，Dafalias Y F.Bounding surface plasticity.Ⅲ：application to anisotropic cohesive soils［J］.Journal of Engineering Mechanics，1986，112（12）：1292.

［3］ Liang R Y，Ma F G.Anisotropic plasticity model for undrained cyclic behavior of clays ［J］.Journal of Geotechnical Engineering，1992，ASCE，118（2）：227.

［4］ Whittle A J. Evaluation of a constitutive model for overconsolidated clays［J］.Geotechnique，1993，43（2）：289.

［5］ Wheeler S J，Naatanen A，Karstunen，et al.An anisotropic elastoplastic model for soft clays［J］.Canadian Geotechnical Journal，2003，40：403.

［6］ Dafalias Y F.Bounding surface plasticity.Ⅰ：mathematical foundation and hypoplasticity［J］.Journal of Engineering Mechanics，1986，112（9）：966.

［7］ Dafalias Y F，Herrmann L R.Bounding surface plasticity.Ⅱ：application to isotropic cohesive soils ［J］.Journal of Engineering Mechanics，1986，112（12）：1263.

［8］ Simo J C，Taylor R L.Consistent tangent operators for rateindependent elastoplasticity［J］.Computer Methods in Applied Mechanics and Engineering，1985，48（3），101.

［9］ Manzari M T，Nour M A.On implicit integration of bounding surface plasticity models［J］.Computers ＆Structures，1997，3（3）：385－395.

［10］ 费康，刘汉龙.边界面模型在ABAQUS的开发应用［J］.解放军理工大学学报：自然科学版，2009，10（5）：447.FEI Kang，LIU Hanlong.Implementation and application of bounding surface model in ABAQUS［J］.Journal of PLA University of Science and Technology： Natural Science Edition，2009，10（5）：447.

［11］ Stipho A S A.Experimental and theoretical investigation of the behavior of anisotropically consolidated kaolin ［D］.Cardiff：Cardiff University，1978.

［12］ Ling H I，Yue D Y，Kaliakin V N，et al.Anisotropic elastoplastic bounding surface model for cohesive soils［J］.Journal of Engineering Mechanics，2002，128（7）：748.

［13］ Leoni M，Karstunen M，Vermeer P A.Anisotropic creep model for soft soils［J］.Geotechnique，2008，58（3）：215.

［14］ Yin Z Y，Chang C S，Karstuene，et al.An anisotropic elasticviscoplastic model for soft clays［J］.International Journal of Solids and Structures，2010，47（5）：665.