直接驱动机器人的函数链神经网络－PD复合控制

贺红林 刘文光 汪 洋

1.南昌航空大学，南昌，330063 2.中国科学技术大学，合肥，230026

0 引言

机器人轨迹跟踪控制的基本要求是精密性和鲁棒性，但因机器人是高度非线性强耦合系统，要实现上述目标并非易事，对于直接驱动机器人(direct drive robot，DDR)则更是如此，这是因为在DDR中并无减速机构可对其外部扰动与关节间的非线性耦合进行衰减。要实现DDR精密控制就必须针对其非线性动力学特性设计控制器，设计方法有两种:一是利用线性化模型替代DDR的非线性模型;二是采用反馈线性化法将机器人模型进行线性化［1］。前者完全忽略关节间的耦合，控制精度低;后者根据机器人模型并利用反馈线性化去除关节间的动力耦合，计算力矩(CT)法即为此类方法。在机器人精确建模的前提下，CT法可实现精密轨迹跟踪。然而机器人的精确模型却很难得到，一方面是因DDR臂杆系统的实际参数，如臂杆质心位置、转动惯量和负载难以确知，存在参数不确定性;另一方面，机器人的外部扰动和摩擦过程更难把握，存在非参数不确定性。DDR控制的关键就在于消除两类不确定性。目前针对前者的主要措施是自适应技术;针对后者则是通过提高系统鲁棒性来容忍它。在上述解决方法的框架下，人们提出了多种算法，其中较典型的是各种基于CT的自适应法，这些方法兼具CT与自适应控制的优点，但它们或要求加速度可测或要求机器人惯性阵可逆，从而影响了其应用［2-4］。

近年来人们将人工神经网络(ANN)引入机器人，推出了许多新的控制方法［5-8］。这些方法大多利用ANN逼近机器人的整个动力学模型，也有少数方法保留机器人标称模型而采用ANN补偿模型的不确定部分，但它们或要求惯性阵精确已知，或要求加速度反馈，有的甚至还要求ANN上的权值具有已知上界。这些方法通常都采用了多层前馈ANN，计算量大、实时性差、不利于在线实现。针对这些问题，本文在DDR上引入函数链神经网络(functional link neural network，FLNN)与PD复合的方法并利用FLNN逼近机器人的模型，实现了机器人的精密控制。

1 机器人动力学模型

1.1 运动方程

DDR的臂杆系统由多根连杆构成，系统的各关节均通过直接驱动电机进行驱动。对于自由度为n的 DDR，其动力学模型可根据 Euler－Lagrange 方程推导出［9］，即

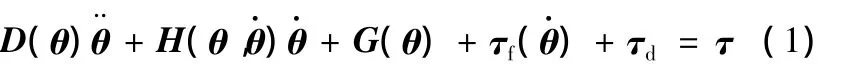
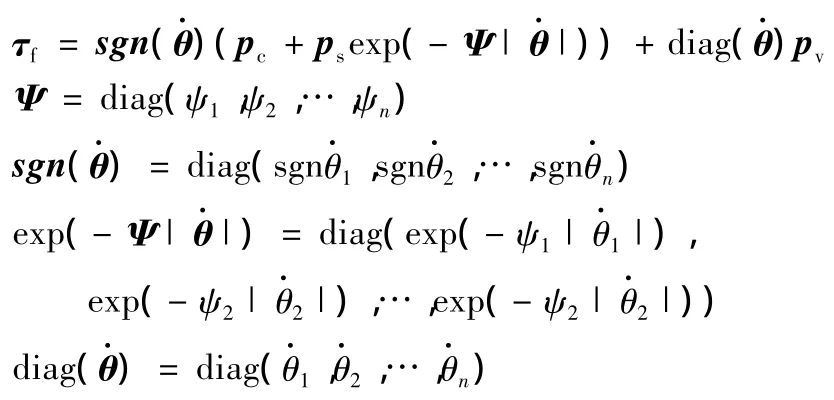
式中，pc、pv分别为关节系统的库仑摩擦力矩和黏性摩擦力矩;ps为黏滞 － 滑动摩擦矢量;ψi(i=1，2，…，n)为常系数。

对于直接驱动机器人而言，pc、pv、ps具有较大的不确定性。

1.2 特性与假定

作为拉格朗日系统，DDR的动力学模型存在一定的结构特性。在设计机器人控制器时需利用这些特性及下面的合理性假定。

特性1 D(θ)具有一致有界，即总存在正常数 μ2＞ μ1＞ 0，使 μ1≤ ‖D(θ)‖ ≤ μ2。

假定1 机器人的重力矩 G(θ)有界，即‖G(θ)‖ ≤ gB，其中，gB为常数。

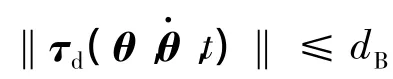
2 控制器的设计

2.1 控制系统结构

为了设计机器人精密轨迹跟踪控制器，有必要引入广义轨迹跟踪误差，即令

式中，θd∈Rn为机器人在关节空间内的期望轨迹;e∈Rn为关节位置偏差为角速度偏差，λ∈Rn×n为适当取定的常值正定阵。

机器人的轨迹跟踪控制器设计就是要确定控制力矩τ的适当形式，使机器人的实际运行轨迹θ(t)→θd(t)。引入了广义跟踪误差后，机器人控制即是要使

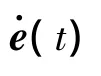
为实现关节系统的控制，本文在机器人上引入一个由PD控制器和神经网络组成的复合控制器，并为其构建图1所示的控制系统。根据该系统的结构，并利用式(1)和式(2)中的关系，可推导出该系统的误差动力学方程

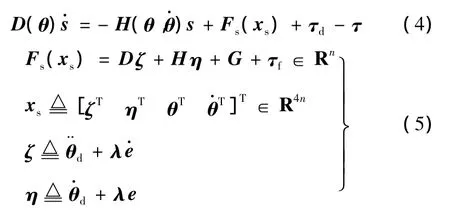
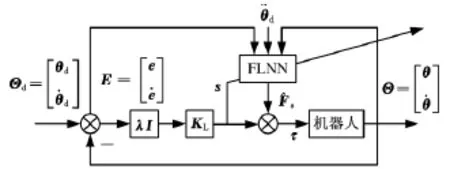
图1 机器人的神经网络控制系统

2.2 控制方案

根据图1给出的系统控制逻辑，可以写出该机器人关节控制力矩的输出形式［8］

其中，τL为线性控制器的输出;KL∈Rn×n为适当取定的正定增益阵;τN为函数链神经网络的输出，该网络拓扑结构由图2给出，其输出形式为

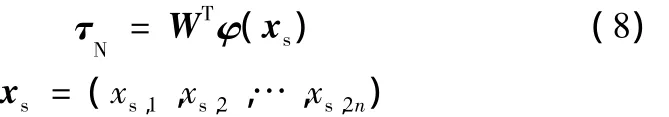
式中，W为网络的理想权值阵;φ(·)∈Rl为神经元激活函数;l为隐层节点数。

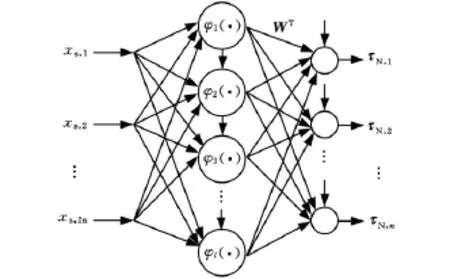
图2 函数链神经网络

本文引入FLNN的目的在于对Fs(xs)进行估值。由于FLNN中只有W可调，故它不像多层前馈网络那样具有广泛的函数逼近能力，但FLNN结构简单、运行效率高，特别是当φ(·)取定为基函数向量时，它同样具有较强的函数逼近能力。φ(·)成为基函数的条件是:设D是关于机器人关节运动状态变量的xs上的列紧子集，映射φ:D→Rn有界可积。若存在有限维数 FLNN，使得C2n(D)内的函数可表示成式(7)形式且使网络输出在C2n(D)中是稠密的。那么φ(·)为C2n(D)中的一组基。

如果φ(·)取为基函数，则对于机器人动力学函数Fs(xs)∈C2n(D)，总存在一定拓扑形式的FLNN，该FLNN能以给定精度εN对Fs(xs)进行逼近，即总存在以下关系

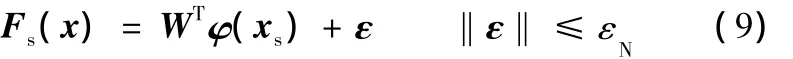
式中，ε为函数估值误差。

FLNN的基函数可取sigmoid函数或径向基函数。本文根据基函数条件自行设计基函数。

2.3 权值学习算法

FLNN控制器设计的关键在于其权值学习律的确定。网络权值的学习不仅应使系统跟踪误差足够小，而且应保证权值的有界性。为了设计权值学习律，构建如下Lyapunov能量函数:

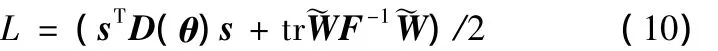
将式(10)对时间进行求导，可得

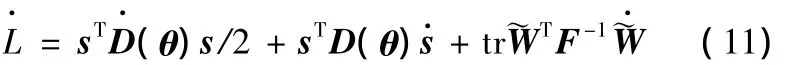
将式(9)、式(8)、式(6)、式(4)代入式(11)并考虑机器人的斜对称特性，可得

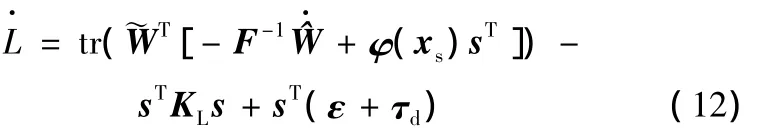
在式(12)中，若令网络权值按下式调整:

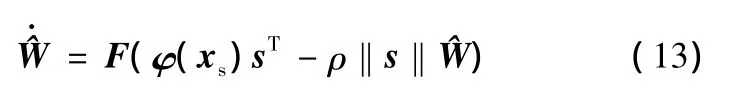
这里的ρ是适当取定的较小正数。这样便可将式(12)将改写成以下形式:

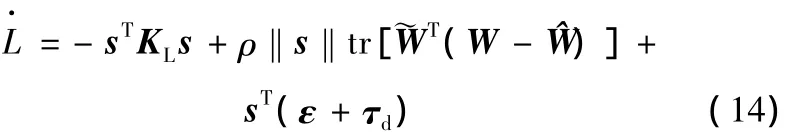
由于式(14)中的方阵求迹运算满足

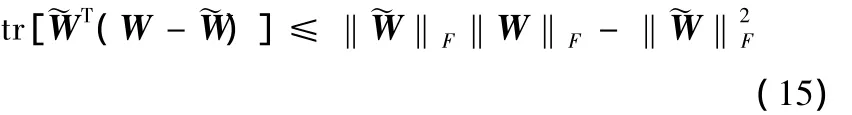
因此，若将式(15)代入式(14)则将得到

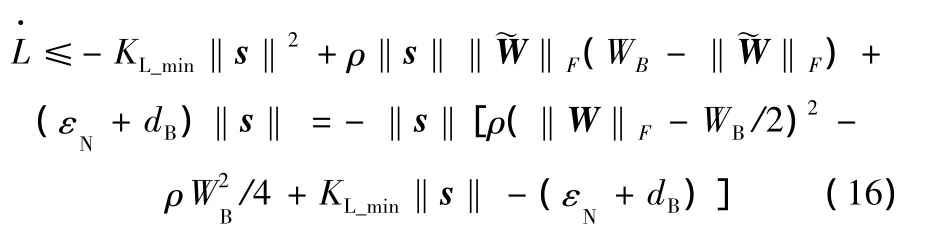
式中，KL_min为矩阵KL中的最小元素的值;dB为系统外部扰动量的上界。

式(16)表明，一旦轨迹跟踪误差越界，即当

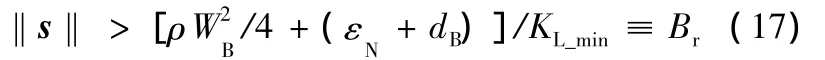
或当网络权值偏差出现以下情况:

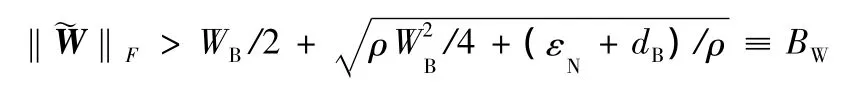
2.4 权值的初始化

网络权值的初始化是FLNN控制器设计中必须考虑的重要问题。但本文的控制系统按式(6)的形式确定机器人的控制作用时，其网络的初始权值可全部设为0。之所以可作这种简单处理，主要是因为在本文的系统中，除了设置有FLNN控制器之外，还引入了一个PD线性反馈补偿器。在系统启动工作初期，由于网络权值为0，因此FLNN基本上不起控制作用，此时系统通过PD控制器实施控制，但FLNN在经过短暂的权值学习后将逐渐发挥作用，并将最终主导机器人的控制。

2.5 网络功能分解

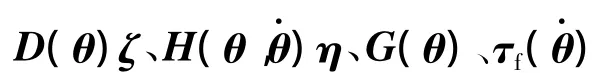
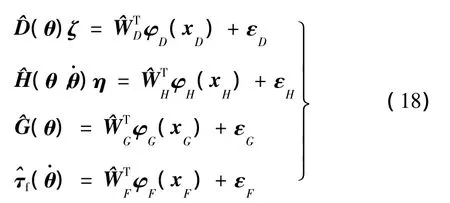
式中，xD、xH、xG、xF分别表示各 FLNN子网的输入;εD、εH、εG、εF表示各子网的估值误差。

当采用子网对Fs(x)进行估值时，估值误差即为各子网估值误差的和。

2.6 控制实现结构

求解式(16)便得到系统的仿真实现形式:

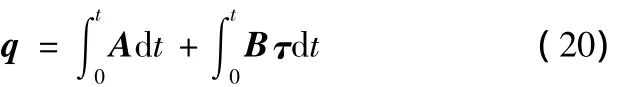
3 控制仿真实验

3.1 仿真对象

为验证上述控制算法的可行性及有效性，针对图3所示机器人臂杆系统进行了控制仿真。该系统由4根臂杆组成，自由度为2。图3标示出杆i的杆长li、质量mi、质心位置lci以及绕自身质心的转动惯量Ii。该机器人的运动方程为

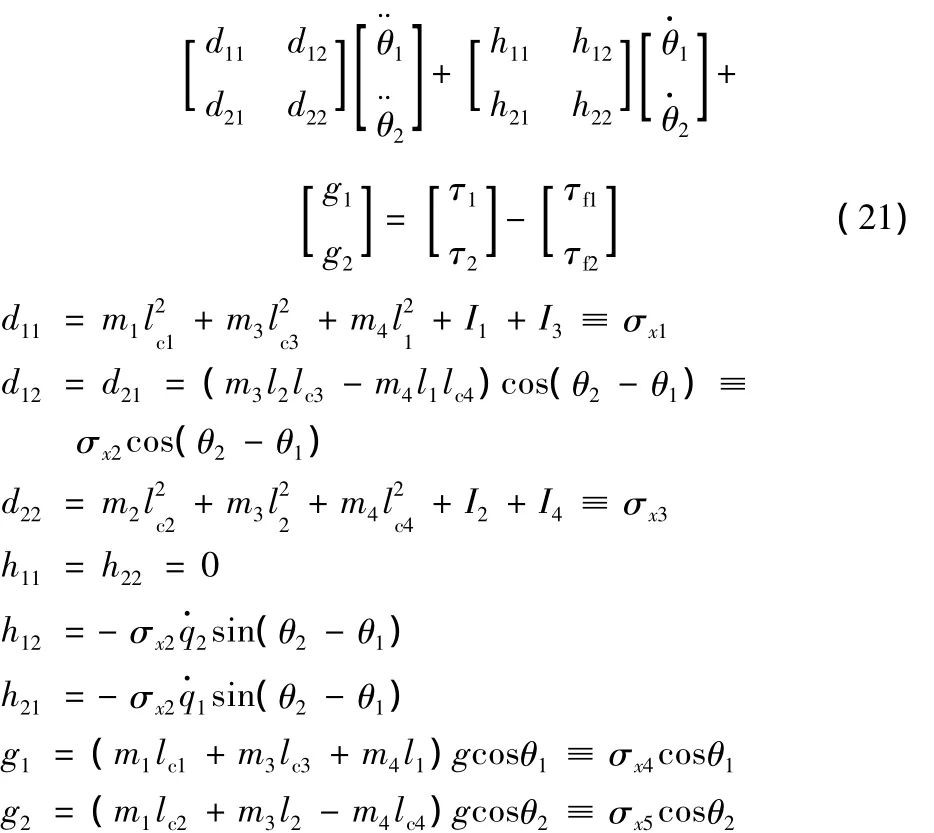
图3中各臂杆的质心位置及其转动惯量无法确知，即动力学模型中的 σx1、σx2、σx3、σx4、σx5存在一定不确定性。但在系统仿真时，可设定其真值为

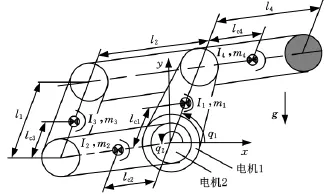
图3 仿真实验用机器人臂杆系统

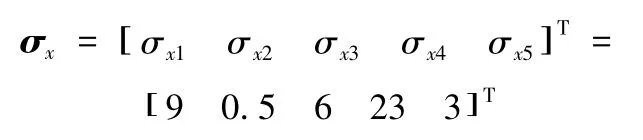
仿真用机器人的摩擦特性参数的真值、目标轨迹θd(t)和外力矩扰动τd分别按下式取定:

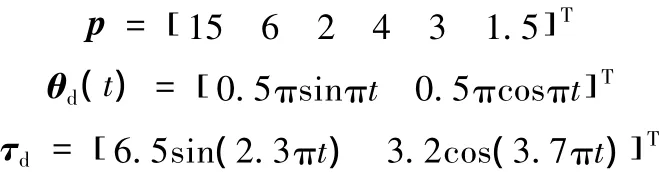
3.2 子网的基函数设计

根据式(18)中各动力学项的结构，可以设计出其相应的FLNN子网的拓扑及基函数结构。本文设计的用于逼近Fs(x)中4个分量的子网的结构如图 4所示(⊗ 表示乘法器)，图中，ζ=［ζ1ζ2］，对应的基函数向量分别为

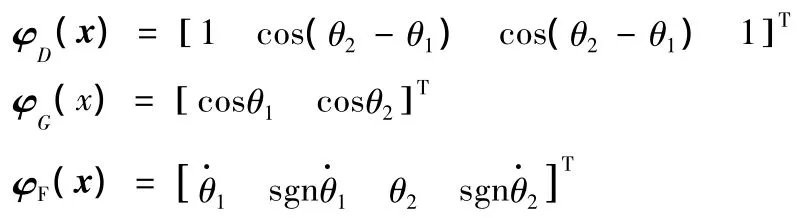
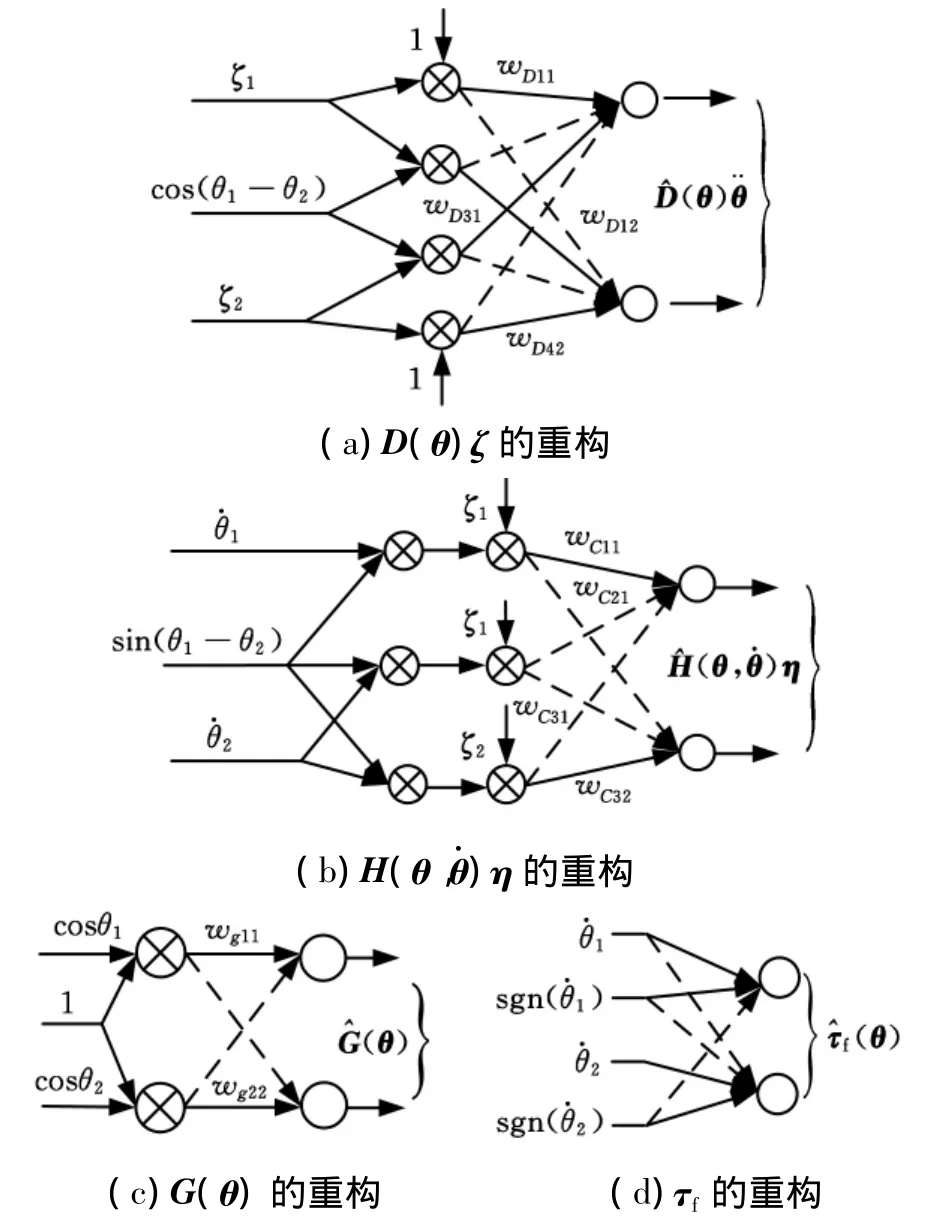
图4 二自由度直接驱动机器人的FLNN子网

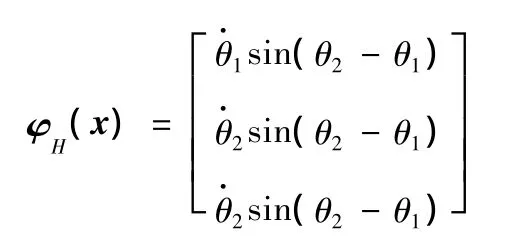
3.3 仿真结果

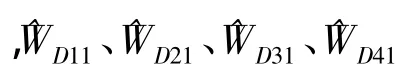
图6给出了按系统标称模型(σ0=［6 0.2 4 13 4］T)进行控制仿真时的结果，不难看出虽然该系统动力学模型的标称值与真值之间的差距较大，但按模型的标称值和真值进行仿真时，其轨迹跟踪精度并无多大差别，之所以如此，主要是因为系统能通过调整权值，较好地减小臂杆系统的参数误差所带来的影响。

图7给出了系统无外部扰动时的FLNN－PD控制结果。从图7可见，无扰动时的系统轨迹跟踪误差与系统存在扰动时的跟踪误差比较接近，它说明该复合控制算法对系统的外部扰动具有较好的鲁棒性。

图8给出了机器人系统在PD控制器单独作用时的控制结果，此时系统的转角误差和角速度误差均比较低。造成这种情况的原因主要是因为线性的PD反馈控制器的参数自适应能力较差，故无法很好地减小系统参数不确定性所引入的控制误差。

图9给出了系统在FLNN单独控制时的结果，从图可见，其转角误差和角速度误差比采用FLNN－PD时稍低一些，但却明显高于单独采用PD时的控制精度。

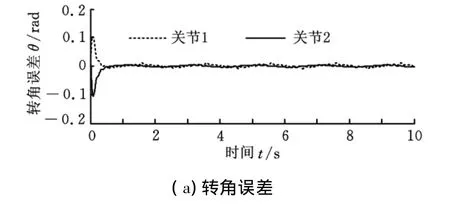
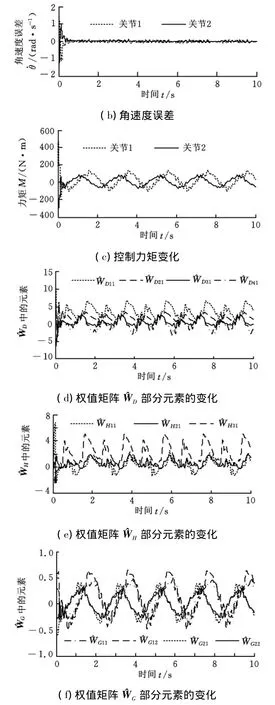
图5 存在外部扰动时的FLNN-PD控制结果

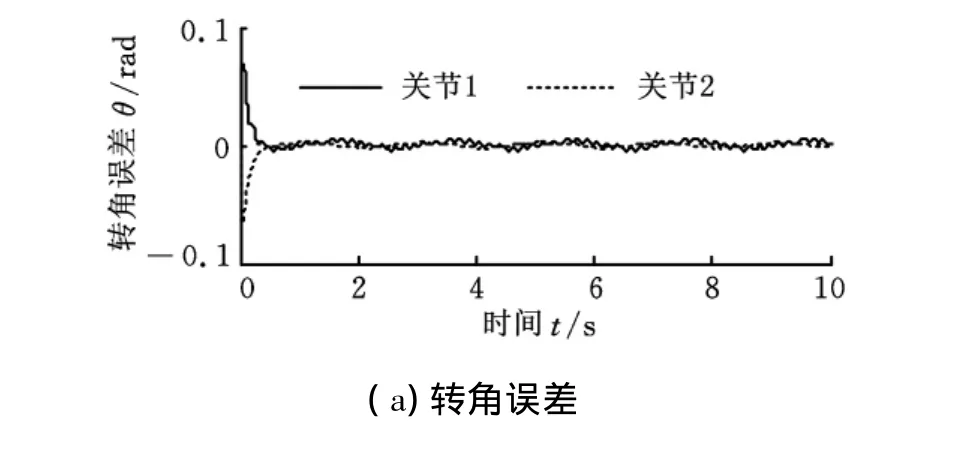
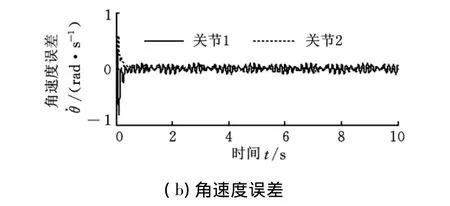
图6 基于系统标称模型仿真的结果

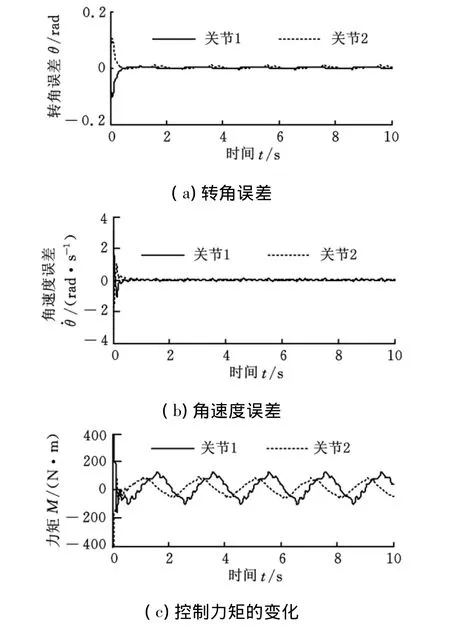
图7 不存在外部扰动时的FLNN-PD控制结果

4 结语

针对直接驱动机器人动力学模型的高度非线性、强耦合及其存在的参数和非参数不确定性，为了实现机器人的精密轨迹跟踪控制，本文引入函数链神经网络对机器人的非确定性动力学量进行逼近，并在此基础上构建出了基于FLNN－PD控制器的机器人双闭环控制系统。通过复合控制结构来减小机器人的非确定性动力学量带来的控制误差，以提高系统的控制精度。文中推导了该系统的控制算法，给出了函数链神经网络控制器的权值学习律，并从理论上证明了FLNN－PD控制器的收敛性及控制系统跟踪误差的收敛性和趋零性。对机器人系统进行了控制仿真，结果显示，采用FLNN－PD控制器可使系统的转角误差和角速度误差控制在±0.002rad和±0.1rad/s之内，并且该控制器对系统的系统参数变化及外部扰动具有较强的自适应性和鲁棒性。研究表明，本文提出的FLNN－PD控制方案既能实现机器人的精密轨迹跟踪，又便于系统的实现，它是一种颇具应用前景的机器人控制方法。

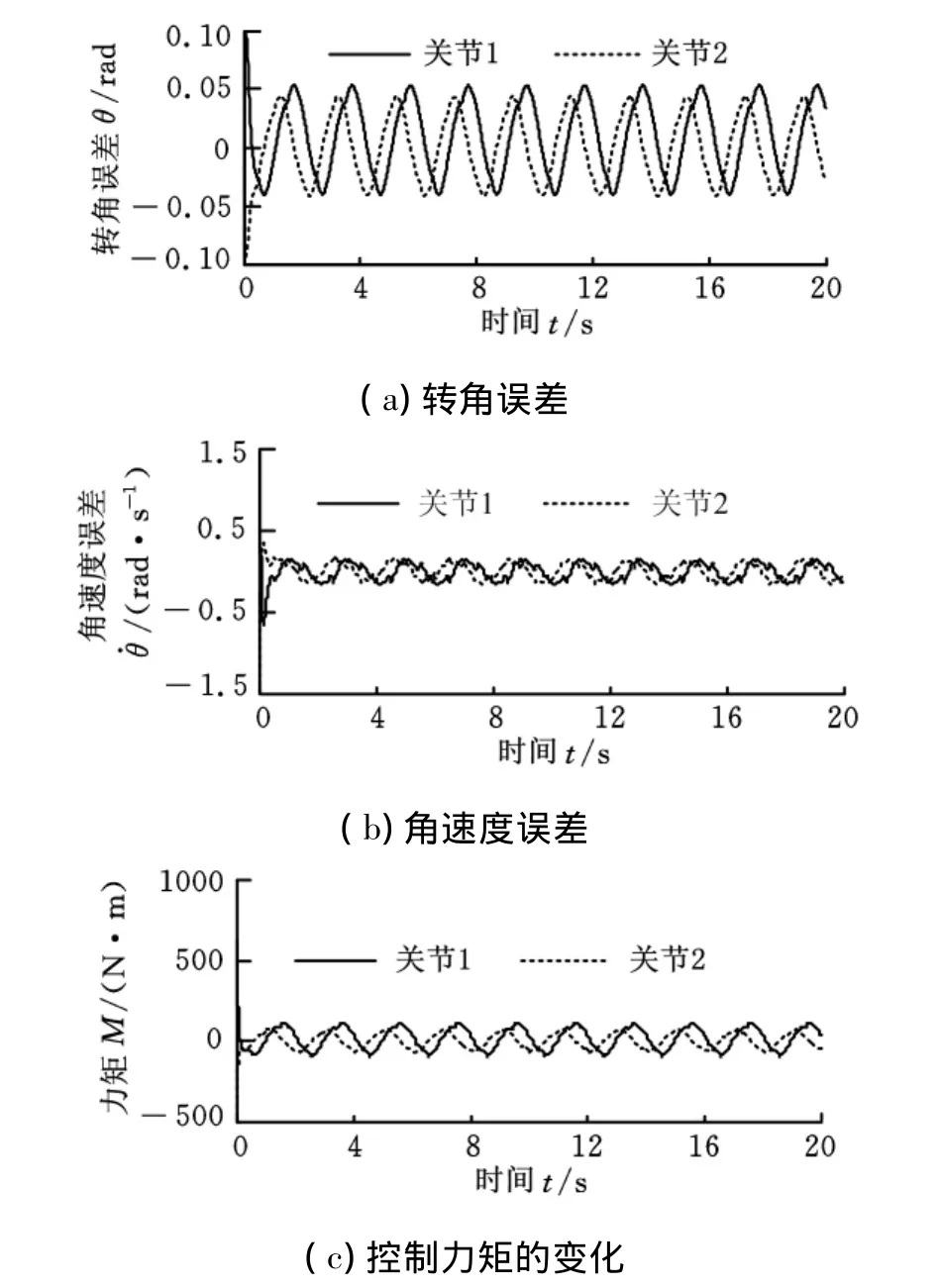
图8 系统单独采用PD时的控制结果(有扰动)

图9 有扰动且单独采用FLNN控制时的结果

［1］谭伟.直接驱动机器人高性能控制器研究［D］.上海:上海交通大学，2000.

［2］Colbaugh R，Glass K.Adaptive Tracking Control of Manipulators:Theory and Experiments［C］//1994 IEEE International Conference on Robotics and Automation.San Diego，CA，USA:2292-2299.

［3］唐晓腾，陈力.自由漂浮双臂空间机器人基联坐标系内的一种增广变结构鲁棒控制方法［J］.中国机械工程，2008，19(19):2278-2282.

［4］张文辉，齐乃明，尹洪亮.不确定机器人的神经网络轨迹控制［J］.自动化与仪表，2010，22(5):22-25.

［5］Cheah C C，Slotine J J E.Adaptive Tracking Control for Robots with Uncertainties in Kinematic，Dynamic and Actuator Models［J］.IEEE Transactions on Automatic Control，2006，51(6):1024-1029.

［6］Barambones O，Etxebarra V.Robust Neural Control for Robotic Manipulators［J］.Automatica，2002，38(2):235-242.

［7］Patino H D，Carelli R，Kuchen B R.Neural Networks for Advanced Control of Robot Manipulators［J］.IEEE Transactions on Neural Networks，2002，13(2):343-354.

［8］Patino D，Liu D.Neural Network－based Model Reference Adaptive Control System［J］.IEEE Transactions on System，Man，and Cybernetics，Part B:Cybernetics，2000，30(1):198-204.

［9］Jiang Zhaohui，Ishita Taiki.A Neural Network Controller for Trajectory Control of Industrial Robot Manipulators［J］.Journal of Computers，2008，3(8):1-8.

［10］De Wit C C.Robust Control for Servo－mechanism under Inexact Friction Compensation［J］.Automatics，1993，29(3):757-761.