踝关节康复机器人设计及人—机运动映射分析

印 松

上海电机学院，上海，200245

0 引言

从运动形式来看，踝关节可视为球铰，具有绕3个垂直轴的转动，即背伸/跖屈、内翻/外翻、内旋/外旋。目前临床使用的踝关节康复训练器结构简单，功能单一，仅提供绕1个轴的转动(背伸/跖屈)，因此康复训练并不全面。从关节运动的原理来看，肌肉群共同作用牵引骨骼产生运动，这与并联机构的工作方式非常相似。此外，并联机构具有高刚性、高承载能力等特点，且能以紧凑的结构实现多个自由度的运动。因此，采用并联机构来实现踝关节康复训练具有广阔的应用前景。近年来，国内外学者对此开展了广泛的应用研究。美国新泽西州立大学研制的Rutgers踝关节康复训练器借助于虚拟现实技术来帮助患者实现踝关节的康复训练［1］。由于其主体结构采用了气压驱动的六自由度Stewart平台，除带来噪声影响之外，还提高了整个设备的复杂性和成本。Dai等［2-4］所开发的踝关节康复机器人采用了3－SPS/S型并联机构。Liu等［5-6］提出的踝关节康复机器人则采用了3－RSS/S型并联机构。上述两类机构本质相同，由于中间球关节的约束作用，该类机构具有与踝关节相同的球面运动特征，但其转动中心与踝关节并不重合，因此可能引起踝关节非预期的运动。通过分析现有踝关节康复机器人的不足，边辉等［7］提出一种新型的2－RRR/UPRR并联机构。通过巧妙的设计，该机构具有远程回转中心，可保证机构转动中心与踝关节重合。这种机构采用了非对称结构，其回转中心固定，不能满足具有不同关节尺寸用户的使用需求。

本文采用基于3－PUS/S型并联机构的康复机器人来辅助病人实现踝关节的康复训练，通过踝关节到机器人的运动映射分析，以解决机器人回转中心与踝关节中心不重合的问题，为实现机器人的有效控制提供了依据。

1 踝关节康复机器人设计

如图1所示，人体踝关节可视为1个具有3个转动自由度(背伸/跖屈、内翻/外翻、内旋/外旋)的球关节。因此，为了全面、有效地实现踝关节的康复训练，机器人应具备球面运动的能力。传统的踝关节康复仪仅提供单个转动自由度，显然不能满足踝关节复杂运动的需要。本文采用3－PUS/S型并联机构来设计踝关节康复机器人。

图1 踝关节运动模型

假定并联机构满足:①机构原动件数等于机构末端执行器的自由度，即原动件数为3，机构既非欠驱动也非冗余驱动;②每个分支运动链仅含1个原动件，即分支运动链数为3;③各分支运动链具有相同的结构形式;④机构动平台与静平台之间通过1个S副(球面副)运动链连接，以保证机构实现绕定点(球面副中心点)的3个转动自由度。

满足以上条件的球面运动并联机构如图2所示。假定各构件之间通过单自由度的基本副连接，Kutzbach Grubler自由度计算公式为

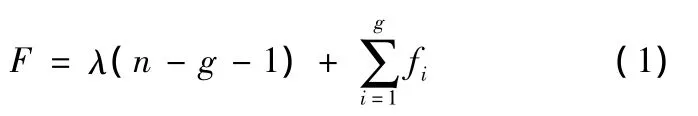
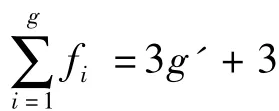
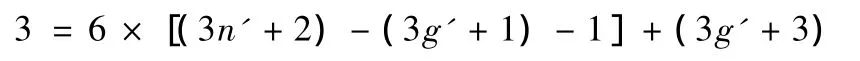
化简得

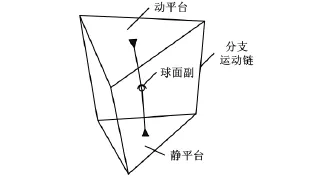
图2 球面运动型并联机构

由于n'和g'皆为整数，因此可取n'=5，g'=6，即该类球面运动并联机构的分支运动链需包含6个单自由度简单副或等价的多自由度运动副，这里选用PUS型运动支链。然而，并联机构属于复杂空间机构，必须考虑各运动链对动平台所产生约束的类型、方向等因素对自由度计算公式所产生的影响［8］。旋量理论在分析机构自由度的数目及自由度的具体性质方面有其独特的优势，下面采用旋量理论来分析3－PUS/S型并联机构的运动特点。

图3所示的3－PUS/S型并联机构中，动平台和静平台之间通过3个对称分布的PUS运动支链连接。包含球铰O的中间支撑链上下端O1、O2分别与动静平台中心固定连接。下角点A1、A2、A3和上角点C1、C2、C3分别均匀布置在半径为r1和r2的圆周上。移动副P汇交于点D，且与静平台形成夹角θ。U副第一回转轴线与静平台平行且与P副方向垂直。在O点建立固定坐标系OXYZ，X轴位于O1A1O2平面内且与静平台平行，Z轴竖直向上。初始状态，动平台与静平台平行且点O、A1、O1、C2和O2位于同一平面内。

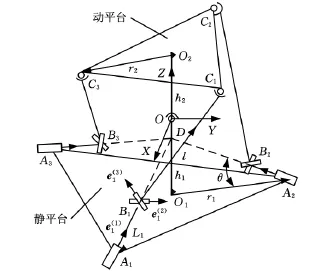
图3 3-PUS/S型并联机构

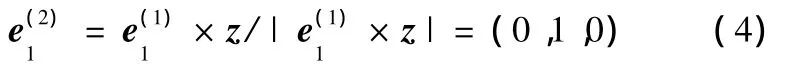
式中，z为Z轴的单位方向向量。

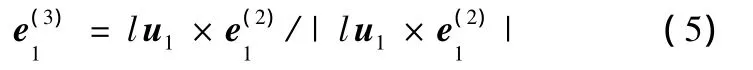
式中，u1为杆B1C1的单位方向向量;l为B1C1的长度，定值。

球铰等价于3个轴线互相正交的转动副，其相关向量可视为

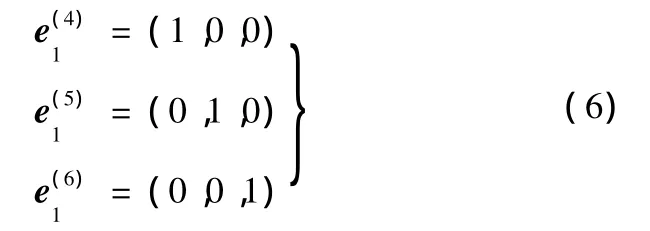
则可得该运动支链运动旋量系:

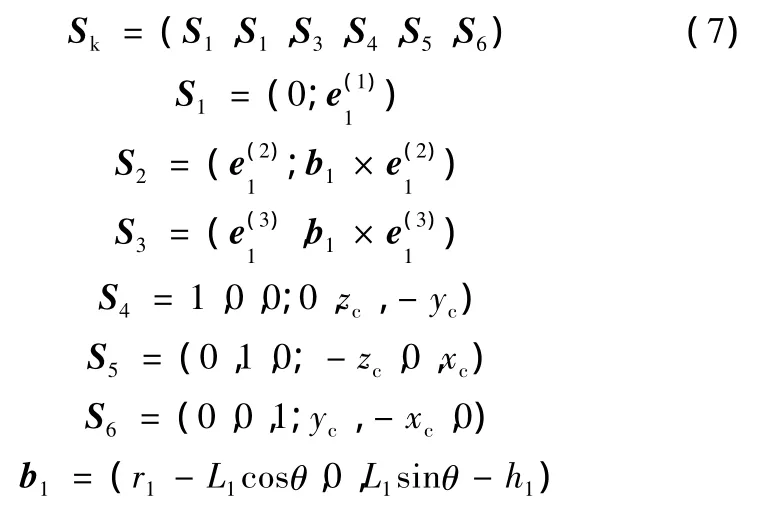
式中，b1为点B1的位置向量;r1为静平台外接圆的半径;h1为球铰中心O到静平台的距离;L1为移动副的位移;c1=(xc，yc，zc)为点 C1的位置向量。

从式(7)可看出，该旋量系线性无关，即

根据互易螺旋理论，该运动支链对动平台无约束作用。对其他两运动支链进行分析可得到同样的结论，即动平台在PUS型运动支链的作用下，可存在任意形式的运动。因此，添加带球铰的中间支撑链即可限制动平台的平移运动。

由上面的分析可知，机构动平台仅存在绕定点的球面运动，该运动方式与踝关节的运动方式相同。

2 运动学分析

对运动链j(j=1，2，3)进行分析，由空间向量关系可得

式中，aj为点Aj的位置向量;c'j为点Cj在动平台坐标系下的位置向量;R为3×3的旋转矩阵。

式(9)两边同时点乘uj可得

当给定动平台的转角信息(α，β，γ)，即可根据式(10)计算出各运动支链移动副的位移。

为了得到机构的速度关系式，将式(9)两边对时间t求导，得

式中，ωj、W分别为杆BjCj和动平台的角速度;aj为一常值向量，其导数为零。

式(10)两端点乘uj，可得

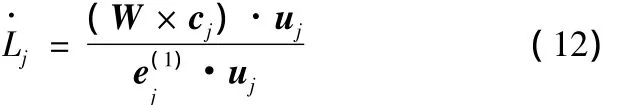
式(12)揭示了输入速度与动平台转速之间的关系，其矩阵的形式为

其中，J为3×3的Jacobian雅可比矩阵。

3 踝关节与机构的运动映射

尽管3－PUS/S型球面运动并联机构具有与踝关节相同的绕定点运动的特点，但其转动中心与踝关节中心并不重合。为了正确、有效地实现康复训练，必须对踝关节和机构的运动映射关系进行分析。

3.1 背伸/跖屈

背伸/跖屈是踝关节的主要运动形式。为了实现该种形式的训练，患者呈坐姿，并将其脚与动平台固定。将机构和患者下肢投影至OXZ平面。由于脚与动平台固定在一起，因此可将其视为一个构件OD，同样，机构静平台和座椅等静止部件可用构件OF来代替。这样，就可得到图4所示的平面四杆机构ODEF。

图4 踝关节背伸 /跖屈运动分析简图

对四杆机构ODEF进行分析，得

消除式(14)中的角度σ，可得

动平台绕Y轴的角位移可表示为

式中，δ0为DO和OF的初始夹角。

背伸/跖屈角位移βf为Z轴和小腿DE之间的夹角:

当给定了背伸 /跖屈角位移，即可通过式(10)、式(15)～式(17)来计算驱动器位移Lj。

3.2 内翻 /外翻

为了实现内翻 /外翻训练，将机构和患者下肢投影至OYZ平面，得图5。图5中，同样可得到一个近似的平面四杆机构ODEF。通过对该四杆机构进行分析，可得

式中，α为动平台绕X轴的转角;φ1为内翻 /外翻运动角位移。

一旦给定内翻/外翻运动转角，就可通过式(10)、式(18)来计算驱动器位移Lj。

图5 踝关节内翻/外翻运动分析简图

3.3 内旋 /外旋

为研究踝关节内旋/外旋运动与机器人运动的映射关系，将机构动平台和患者下肢投影至OXY平面，得图6。图6中，患者脚随动平台C1C2C3绕Z轴转动，D0O和DO分别为脚初始方向和转动后的方向，其夹角∠D0OD即为踝关节内旋 /外旋运动转角。由图6可知，转角∠D0OD与动平台欧拉角γ相等。

图6 踝关节内旋/外旋运动分析简图

4 仿真实验

设相关参数如下:a=200mm，b=400mm，c=450mm，d=800mm，a1=200mm，b1=200mm，c1=100mm，d1=300mm，δ0=40°，∠O2OF=60°，在 MATLAB中建立各转角关系式，当背伸/跖屈、内翻/外翻运动变化范围为［－30°，30°］时，仿真结果如图 7、图8 所示。

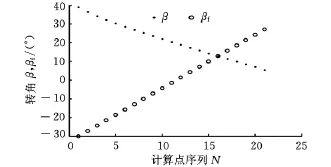
图7 背伸/跖屈运动

图8 内翻/外翻运动

由图7可见，背伸/跖屈运动与动平台绕Y轴的转动并不相同，当背伸/跖屈运动线性均匀变化时，β呈非线性非均匀变化。因此将机器人回转中心等同于踝关节中心，将导致错误的控制结果。内翻/外翻运动(图8)可得到同样的结论。

5 结语

采用自由度分析方法，设计了具有球面运动能力的并联机构来辅助踝关节实现康复训练。旋量理论分析表明，机构的PUS运动支链不对动平台产生任何约束，具有与踝关节相同的球面运动的能力。在建立机构逆运动学的基础之上，将机构与人体下肢视为平面四杆机构。通过对该平面四杆机构的分析，得到踝关节到机构的运动映射关系。数值仿真表明，机器人回转中心与踝关节中心不重合，人－机运动映射有助于正确、有效地实现踝关节的康复运动控制。

［1］Girone M，Burdea G，Bouzit M，et al.A Stewart Platform －based System for Ankle Telerehabilitation［J］.Autonomous Robots，2001，10(2):203-212.

［2］Dai J S，Zhao T S，Nester C.Sprained Ankle Physiotherapy Based Mechanism Synthesis and Stiffness A-nalysis of a Robotic Rehabilitation Device［J］.Autonomous Robots，2004，16(2):207-218.

［3］Saglia J A，Tsagarakis N G，Dai J S.Inverse－kinematics－based Control of a Redundantly Actuated Platform for Rehabilitation［J］.Journal of Systems and Control Engineering，2009，223(1):53-70.

［4］Saglia J A，Tsagarakis N G，Dai J S.A High Performance 2－dof Over－actuated Parallel Mechanism for Ankle Rehabilitation［C］//Proceedings of the IEEE International Conference on Robotics and Automation.Kobe，Japan，2009:2108-2186.

［5］Liu G Q，Gao J L，Yue H，et al.Design and Kinematics Simulation of Parallel Robots for Ankle Rehabilitation［C］//IEEE International Conference on Mechatronics and Automation.Luoyang，China，2006:1109-1113.

［6］Liu G Q，Gao J L，Yue H，et al.Design and Kinematics Analysis of Parallel Robots for Ankle Rehabilitation［C］//IEEE International Conference on Intelligent Robots and Systems.Beijing，2006:253-258.

［7］边辉，刘艳辉，梁志成，等.并联2－RRR/UPRR踝关节康复机器人机构及其运动学［J］.机器人，2010，32(1):6-12.

［8］赵景山，冯之敬，褚福磊.机器人机构自由度分析理论［M］.北京:科学出版社，2009.