用CFD方法研究具有通用膜厚方程径向轴承的动压特性

庞晓平 牛 坤 魏思远

重庆大学机械传动国家重点实验室，重庆，400030

0 引言

现代机器不断向高速、大功率方向发展，对滑动轴承性能的要求也不断提高，许多学者开始研究非圆轴承。有学者研究了表面波浪对一般圆轴承润滑性能的影响［1］，还有学者研究了带沟槽的滑动轴承、螺旋沟径向滑动轴承、球形滑动轴承或锥形滑动轴承，以及阶梯瓦面结构轴承等非圆轴承［2-4］，他们都在寻找大承载力的滑动轴承。文献［5］采用有限差分算法计算径向轴承的承载力，得出了非圆轴承的性能优于圆轴承的结论。本文在文献［5］的基础上，用 CFD软件 FLUENT和COMSOL Multiphysics分析计算了雷诺边界条件下的承载力以及轴承的其他性能参数，进一步论证基于泛函的动压轴承型线集成理论的正确性。

1 基于泛函的动压轴承型线集成理论

轴承的动压润滑:轴与轴颈之间的润滑流体在轴旋转运动时形成动压，以此来承受外载荷并免除相互接触，从而起到减小摩擦阻力和保护轴承表面的作用［5-7］。形成动压的几何条件是:①轴承与轴颈表面之间具有楔形间隙;②两者表面具有相对运动。如图1所示。

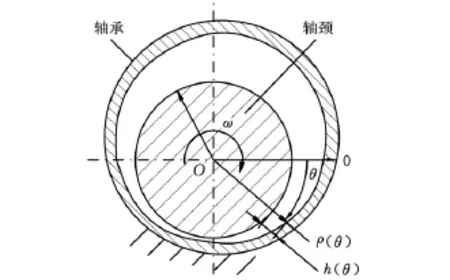
图1 动压轴承楔形间隙示意图

根据现有动压轴承型线表达式的共有特性，型线方程可表示为

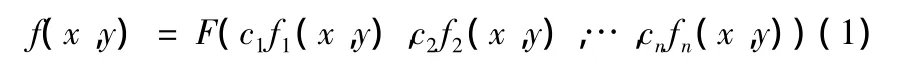
式中，f1(x，y)、f2(x，y)、…、fn(x，y)为由现有所有动压轴承型线级数表达式中同方次项的同类项所组成的函数;c1、c2、…、cn为待定系数。

由此建立统一的动压轴承轮廓线的广义泛函方程，用该广义泛函方程表征任意可能的动压轴承型线［8］。为简化方程，可用傅里叶级数表示为

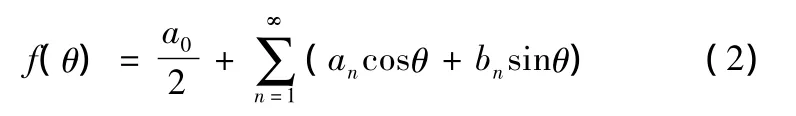
式中，a0、an、bn为待定系数;θ为转角。

显然式(2)是周期为2π的周期函数，而且满足动压轴承形成动压的楔形间隙几何条件。式(2)既可表示现有经典的轴承形状，也可扩展出新的轴承形状，可称为基于泛函的通用动压轴承型线方程。这里假设轴承内充满润滑液体，使油膜厚度方程可由型线方程直接表示。因此图1中

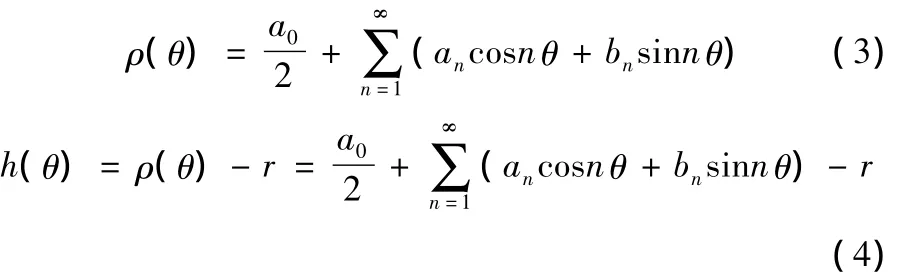
设h0为最小油膜厚度，则量纲一通用膜厚表达式为

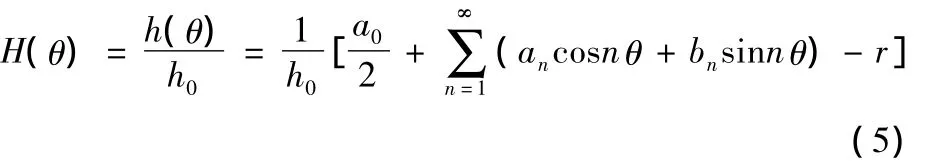
2 FLUENT和COMSOL的数学建模与分析

本文以简化后的基于泛函的动压轴承型线集成理论的模型为研究对象。为了便于比较，圆轴承(n=1)和非圆轴承(n=3)的轴承通用膜厚的型线方程参数与文献［5］相同。d为轴承内径，B为轴承宽度，n'为转速。润滑油牌号为HU220，ρ为润滑油密度，μ为平均动力黏度，T为平均工作温度。计算时忽略黏度随温度的变化。边界条件:p1为进油压力，p2为出油压力，从两侧油槽进油，轴承两端出油，其他部分为固壁边界。具体参数值如表1所示。

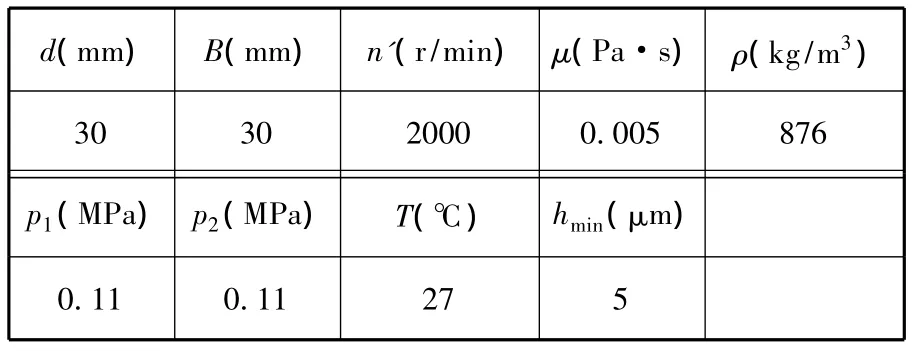
表1 轴承模型参数设置

文献［6］以式(5)的系数为优化变量，以最大承载力为优化目标，用遗传算法优化得出n=3的非圆型线轴承的最大承载力大于n=1的圆型线轴承的最大承载力，具体的型线方程系数优化结果如下:

当n=1时，优化后的量纲一型线方程为

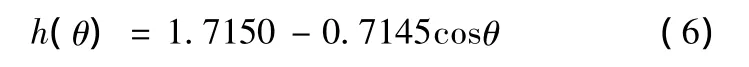
当n=3时，优化后的量纲一型线方程为

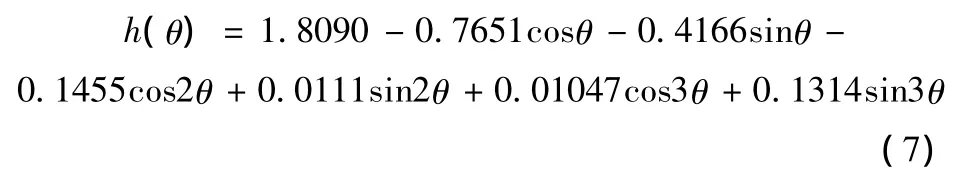
优化结果计算的承载力、油泄、功率损失如表2所示。

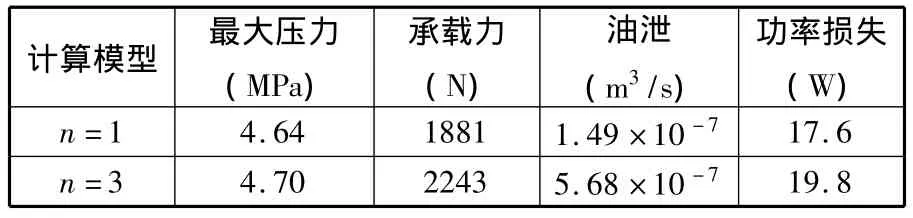
表2 文献计算不同模型的结果比较

当n=1和n=3时，油膜厚度曲线如图2所示。

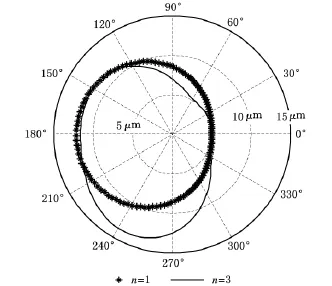
图2 n=1和n=3的油膜厚度曲线

2.1 FLUENT数学模型的建立与结果比较

本文基于泛函动压轴承型线方程建立圆轴承与非圆轴承的几何模型(式(6)、式(7))，采用六面体结构化划分网格单元。由于轴承油膜非常薄，其与半径和轴承宽度相比为极小量，易造成网格扭曲大和最小体积为负，从而降低网格质量，影响计算的结果，因此综合考虑网格质量及计算时间的影响，经过反复试验，本文的研究模型网格的总数量为210 000，这样可以得到较好的网格质量和足够的精度，计算时间相对较短。轴承网格结构如图3 所示［9-10］。

从Gambit中输出网格，并导入FLUENT求解器中进行迭代求解。分别得出了n=1和n=3时油膜压力的分布，如图4、图5所示。

图3 Fluent建模的轴承结构网格图

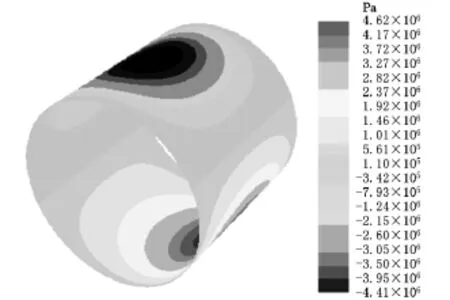
图4 Fluent计算n=1油膜压力分布图

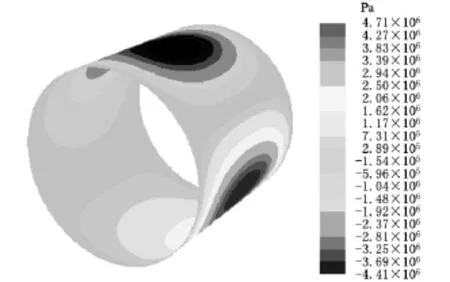
图5 Fluent计算n=3油膜压力分布图

从图4、图5可以看出，最小油膜厚度附近油膜压力最大;在整个上半圆周区域内，出现深色负压区;整个下半圆周区域内，出现深色正压区，这是由于轴颈偏心旋转和挤压作用所引起的。在负压区内，油膜会破裂，实际压力为0。

通过FLUENT后处理功能分别导出压力，用MATLAB编写雷诺边界条件下的油膜承载力的程序。将导出的压力数据带入编写的程序中进行运算求解，分别得出雷诺边界条件下的油膜承载力，具体方法是从FLUENT中输出油膜的压力及坐标数据，然后导入到MTALAB中进行处理，先把三维坐标转化成二维坐标，即把曲面转化为平面。采用负压归零法，压力为负数的即赋值为零，再对平面进行积分，变换公式为

式中，x'为产生的平面新坐标值;r为位置半径;(x，y)为轴承截面的坐标。

最后用FLUENT计算出轴承的油泄、功率损失相关参数，如表3所示。

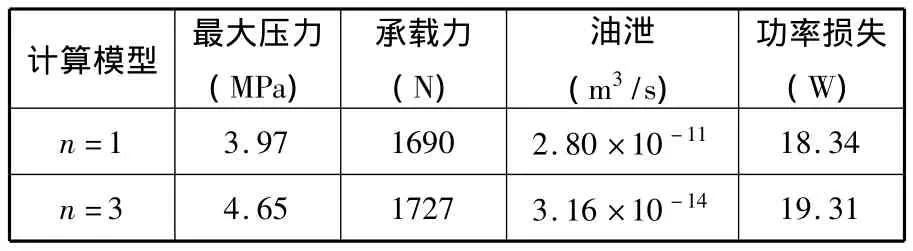
表3 Fluent计算不同模型的结果比较

从表3可以看出，n=3时的非圆轴承雷诺边界条件下的承载力比n=1时的圆轴承的承载力大，得到的其他数据与基于泛函的动压轴承型线集成理论所得到的数据趋势一致。因此，用FLUENT软件得到的结果验证了基于泛函的动压轴承型线集成理论的正确性。

2.2 COMSOL Multiphysics数学模型的建立与结果比较

COMSOL Multiphysics是专为同时描述和模拟多种物理耦合现象而开发的、基于有限元分析的软件包，可使用其中的润滑壳模块对径向滑动轴承进行求解分析［11］。与其他常用的有限元分析软件不同，COMSOL从MATLAB中的Toolbox发展而来，因而它保留了同MATLAB的完善接口，可以与MATLAB完全兼容，这就为用户建模和仿真优化设计带来了方便，也为进一步的应用提供了更大的灵活性。

在COMSOL Multiphysics中，首先建立简化之后的几何数学模型，COMSOL采用的是参数化交互式建模，通过输入式(6)或式(7)，建立数学模型，然后划分网格，如图6所示。参数化交互式建模只需修改基本参数和通用膜厚方程即可修改模型，大大节省了研究时间，提高了工作效率。最后求解得到轴承n=1和n=3的压力分布，如图7、图8所示。

图6 COMSOL建模轴承网格结构图

采用与Fluent软件相同的处理方法，计算出轴承的相关参数，如表4所示。

图7 COMSOL计算n=1油膜压力分布图

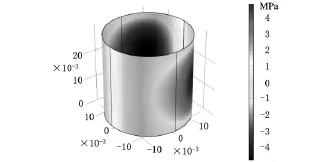
图8 COMSOL计算n=3油膜压力分布图

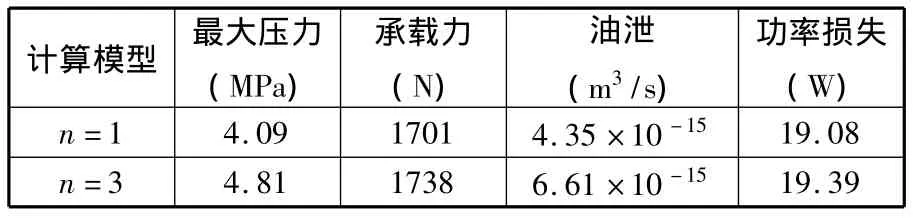
表4 COMSOL计算不同模型的结果比较

从表4可以看出，n=3时的非圆轴承雷诺边界条件下的承载力比n=1时的圆轴承的承载力大，得到的其他数据与基于泛函的动压轴承型线集成理论所得到的数据趋势一致。因此，用COMSOL Multiphysics软件得到的结果也验证了基于泛函的动压轴承型线集成理论的正确性。

从表3和表4中的数据可看到，两种软件计算出的轴承承载力几乎相等，但同表2中由数值分析得到的数据存在一定差异，这是因为在数值分析时为了编程计算简单，以等温、层流、不考虑惯性力等条件下的理想雷诺方程为基础分析压力分布，存在一定误差，但是，无论是数值分析还是软件分析都得到同样的结论，即非圆弧轴承的承载力大于圆弧轴承的承载力。

3 结语

利用CFD软件FLUENT与COMSOL Multiphysics分别建立了径向滑动轴承动力特性计算分析模型，并进行数值仿真，将计算所得到的油膜压力场以三维云图的形式直观地表现出来，揭示了滑动轴承润滑油膜的压力分布规律。通过两种软件对文献［5］优化得到的圆弧轴承和非圆弧轴承进行分析，结果显示:非圆弧型轴承的承载力大于圆弧型轴承的承载力，进一步论证了基于泛函的动压轴承型线集成理论的正确性，为今后分析滑动轴承动力特性提供了借鉴。此外COMSOL Multiphysics具有参数化建模功能，更适合对基于通用型线方程的径向轴承进行流体动力学分析。采用CFD软件分析计算，可大大缩短计算时间，减小误差，充分显示了人机协作的优越性。

［1］Rasheed H E.Efects of Surface Waviness on the Hydrodynamic Lubrication of a Plain Cylindrical Sliding Element Bearing［J］.Wear，1998，223(8):1-6.

［2］Mohsin M E，Seif A A，Shaheen M.The Dynamic Behavior of Fluid Bearings with Grooved Lands［J］.Tribology International，1986，19(3):133-140.

［3］McKenna J M.Journal Bearing with High Stiffness:US，4971459［P］.1990-11-20.

［4］Huang Y，Chen D G.Effects of Partial－grooving on the Performance of Spirl Groove Bearings:Analysis U-sing a Perturbation Method［J］.Tribology International，1996，29(4):281-290.

［5］Pang Xiaoping，Qin Ning，Dwyer－ Joyce R S，et al.A General Profile Parameterization of Hydrodynamic Journal Bearings for Efficient Shape Optimization［J］.Tribology Transactions，2010，53(1):117-126.

［6］张直明，张言羊，谢友柏，等.滑动轴承的流体动力润滑理论［M］.北京:高等教育出版社，1986.

［7］庞晓平，陈进，王家序.采用通用膜厚方程的动压径向轴承形状优化［J］.西安交通大学学报，2009，43(1):57-61.

［8］庞晓平，陈进.基于泛函的动压轴承型线集成理论研究［J］.润滑与密封，2008，33(2):71-74.

［9］高庆水，杨建刚.基于CFD方法的液体动压滑动轴承动特性研究［J］.润滑与密封，2008，33(9):65-67.

［10］马涛，戴惠良，刘思仁.基于FLUENT的液体动静压轴承数值模拟［J］.东华大学学报(自然科学版)，2010，36(3):279-282.

［11］张骅毅，范启富.基于COMSOL和iSIGHT的磁悬浮轴承优化设计［J］.开发应用，2010，26(3):36-38.