金属带式无级变速器钢带环弹性特性及其造成的能量损失
2012-12-03崔亚辉
张 武 刘 凯 崔亚辉 原 园 赵 桐
1.西安理工大学,西安,710048 2.西安科技大学,西安,710054
0 引言
金属带式无级变速器(MB-CVT)作为最成功的无级变速器之一,具有节省燃料、操控简单、驾驶平顺舒适和低排放等优点。最新研究显示:在相同的工作状态下,装备MB-CVT的汽车较装备自动挡的汽车节油7% ~15%[1]。MB-CVT属于摩擦传动系统,因此其传递动力的能力受到一定限制。
Kong等[1]以单个钢带环为基础建立了MBCVT动力学模型,研究了带轮与最内层钢带环以及钢带环之间的相互作用及每层钢带环在传递动力方面的负载分布状况,并且认为一层或多层钢带环过早断裂是变速器失效的一个重要原因。Kuwabara等[2]在研究中忽略了钢带环之间的相互作用,并将其假设为一个整体。Kim等[3]完全忽略MB-CVT各部件间的相互作用,且进一步认为两组钢带环和数以百计的金属块是一个连续体。Akehurst等[4]假设所有的钢带环都具有相同的圆弧段,且每组钢带环是由数层钢带环组合而成,但是对于每层钢带环承载力矩的能力却没有研究。Sun[5]假设所有钢带环不管在圆弧段还是直线段都平均地分担金属带所承受的张力。Micklem等[6]认为每层钢带环都具有相同的速度和张力,但是其研究结果显示最内层和最外层钢带环对传递动力有贡献,其余的钢带环在动力传递方面均无太大作用。Kuwabara等[7]分析了每层钢带环的负载分布和张力变化情况,但是其模型较简单。
本文主要研究钢带环的弹性特性及其造成的变形能损失,建立了MB-CVT和钢带环模型,研究了钢带环应力应变、位移、变形能和功率损失等问题。
1 MB-CVT
1.1MB-CVT 模型
图1所示是由两个带轮和钢带环组成的MB-CVT简化模型。由于研究重点在钢带环上,因此模型对带轮进行了简化处理,并略去了金属块,其中每组钢带环由10层钢带环叠加而成。图1中,Tbc指bc段上钢带环张力,Tad指ad段上钢带环张力。
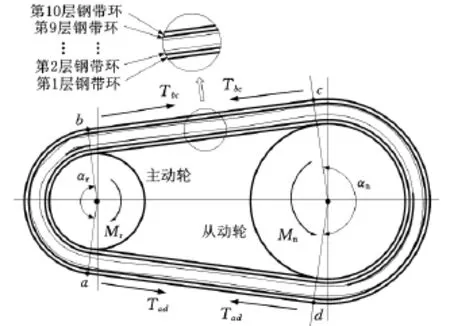
图1 MB-CVT模型
1.2 钢带环模型
在钢带环模型中,主动轮上作用恒定的转速和输入扭矩,从动轮上作用有固定的负载,且均不超过MB-CVT的承载能力。模型的建立还包含以下假设:① 钢带环之间既无间隙也无过盈;②钢带环仅发生弹性变形;③在圆弧段上,作用在钢带环上的压力是均匀的,直线段上钢带环之间无压力;④忽略钢带环工作过程中的离心力。
相关参数如下:弹性模量E=206GPa,泊松比ν=0.25,带轮半楔角θ=11°。带轮轴向推力为F,均匀分布在最内层钢带环上的作用力为F0,其表达式为

1.3 圆弧段上钢带环应力应变、位移和应变能分析
在圆弧段上,通过主从动轮轴向推力计算钢带环受到的均匀压力,由于钢带环横向自由(无约束),因此属于平面应力问题,所以可以将钢带环简化为组合薄壁圆筒模型,如图2所示。
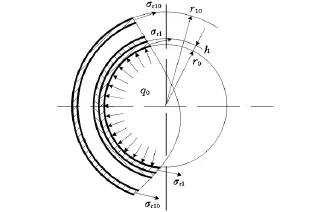
图2 钢带环的组合薄壁圆筒模型
作用在最内层钢带环上的均布压力为

式中,α、r0分别为钢带环在带轮上的包角和带轮节圆半径;wr为钢带环的宽度。
钢带环的应力应变、位移方程如下:
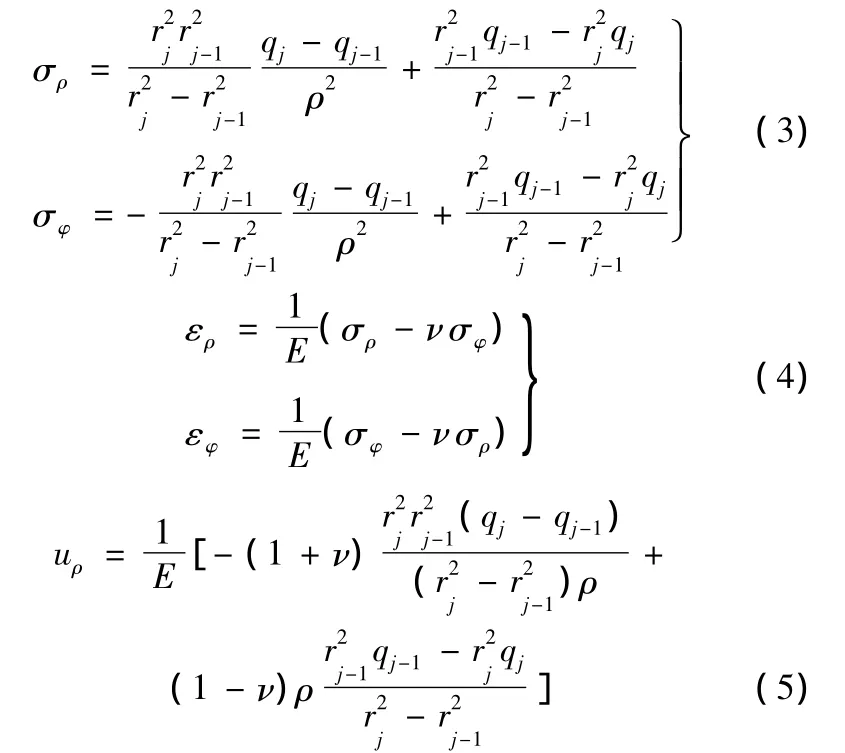
式中,σ为应力;ε为应变;u为位移;ρ为钢带环半径。
其中,角标ρ和φ分别表示径向方向和切向方向,j表示第j层钢带环,取值范围是1≤j≤10。其中:
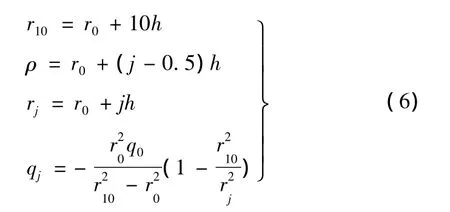
式中,h为单层钢带环厚度。
钢带环应变能密度δ表达式如下:
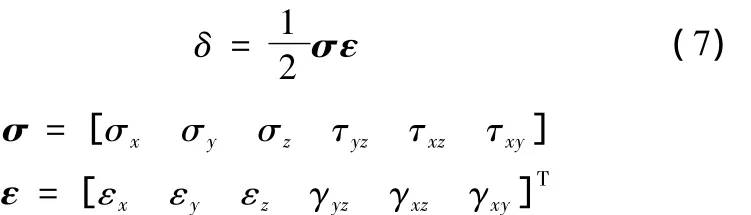
其中,x、y、z为直角坐标系的坐标轴。
结合模型的边界条件,将式(3)和式(4)代入式(7)可得
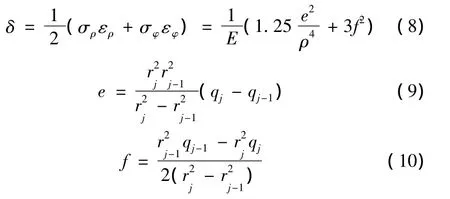
对式(8)进行积分运算可得圆弧段上钢带环的应变能UYH的计算公式:
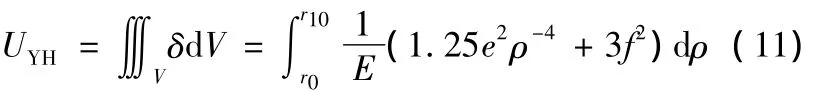
1.4 直线段上钢带环应力应变,位移和应变能分析
在直线段上,与纵向变形相比,钢带环的横向变形可以忽略。因此直线段上的钢带环被简化为单向拉伸问题。相关公式如下:
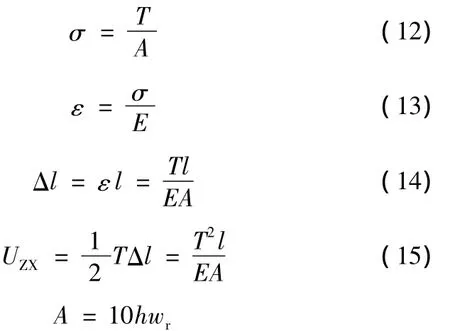
式中,T为钢带环张力,T为Tbc时是指“bc”段上钢带环张力,T为Tad时是指“ad”段上钢带环张力;A为一组钢带环的横截面面积;l为直线段钢带环的原始长度;Δl为各部分钢带环的伸长量。
1.5 钢带环功率损失
金属带的工作区域可以划分为四部分,因此钢带环的伸长量也包含四部分,即为两个圆弧段和两个直线段:主动轮、从动轮圆弧包角范围内钢带环伸长量为Δlr和Δln,bc和ad段钢带环伸长量为Δlbc和Δlad。因此,钢带环总的伸长量
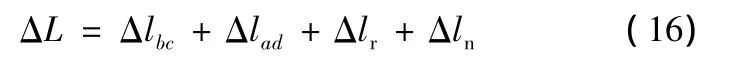

钢带环总的应变能损失
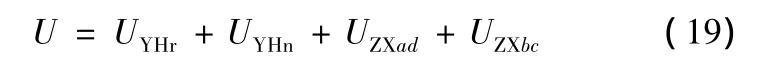
由应变能造成的功率损失

式中,t为应变能损失所用的时间。
2 算例分析与讨论
2.1 计算参数
本节参数取值主要参照参考文献[9]:额定功率P=70kW,最大输入转矩M1=160 N·m,最大输入转速n1=6000r/min,由试验可得其他相关参数,如表1所示。
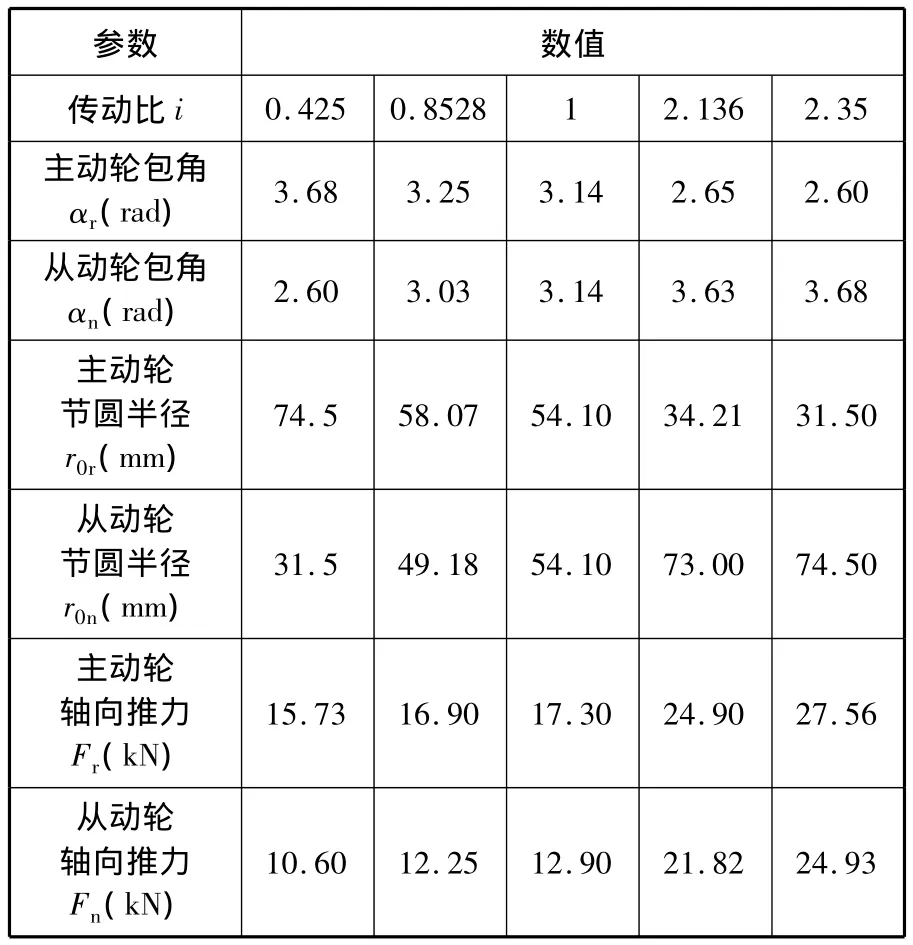
表1 由试验所得参数
2.2 应力应变、位移结果分析与讨论
图3和图4所示为主动轮、从动轮上钢带环的径向和切向应力变化规律。径向应力为负值,所以是压应力。当传动比一定时,径向压应力从最内层钢带环到最外层逐渐减小,并趋近于零。最外层钢带环的外侧无论在主动轮还是从动轮上都是自由面,因此应力为零。随着传动比的增大,钢带环的压应力在主动轮上逐渐增大,在从动轮上先减小后增大。图4所示的切应力属于拉应力。随着传动比的增大,钢带环在主动轮上的切向拉应力也增大,从动轮先减小后增大。由于最内层钢带环的半径是最小的,所以最内层钢带环的切向拉应力最大。因此,当传动比一定时,半径对钢带环切向拉应力的影响较大,且当传动比较小时,切向拉应力变化趋势较平缓。最内层和最外层钢带环切向拉应力是两个疲劳极限值,它们的差值不能太大,否则会缩短变速器的使用寿命。当传动比为2.35时,主动轮上最大差值为1.053(129.3/122.8=1.053,1.0539=1.59)。这个数值已经影响了切向拉应力的均衡性。因此,对各层钢带环进行相应的预置压应力可以在一定程度上解决这一问题。

图3 钢带环的径向应力
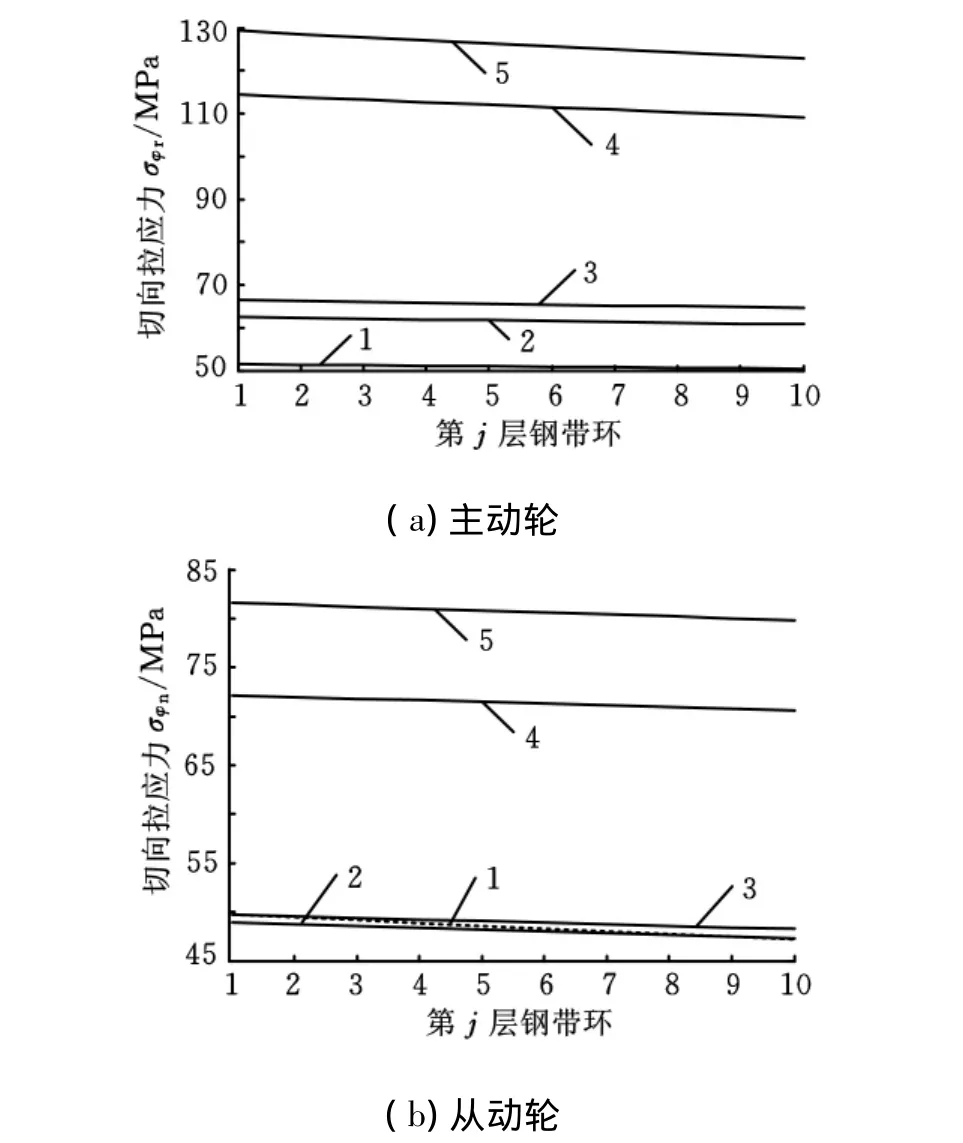
图4 钢带环切向应力
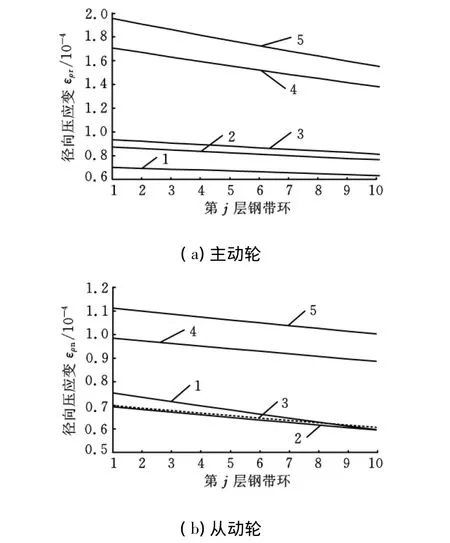
图5 钢带环径向应变
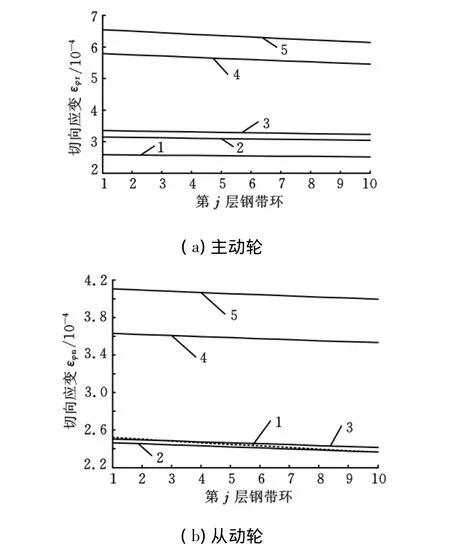
图6 钢带环切向应变
图5和图6所示为主动轮、从动轮上钢带环的径向和切向应变变化趋势。径向压应变从钢带环最内层到最外层依次减小。随着传动比的增大,主动轮上的径向压应变增大,从动轮上则是先减小后增大。最内层和最外层钢带环径向压应变的最大差值发生在传动比为2.35时的主动轮上,因此半径对径向压应变的变化有很大影响。随着传动比的增大,切向拉应变在主动轮上增大,从动轮上先减小后增大。图7所示为主动轮、从动轮轴向推力和节圆半径随传动比的变化趋势[10]。主动轮上的轴向推力是单调下凹上升曲线,节圆半径是单调下凹下降曲线,因此主动轮上的钢带环应力应变表现出严格的单调性。但是在从动轮上,轴向推力是单调下凹上升曲线,节圆半径是单调上凸上升曲线。又因为应力应变和轴向推力为近似正比关系,与节圆半径为反比关系,所以当轴向推力曲线上最凹的部分与节圆半径曲线上最凸的部分相遇时,从动轮上钢带环的应力应变曲线就发生了突变。
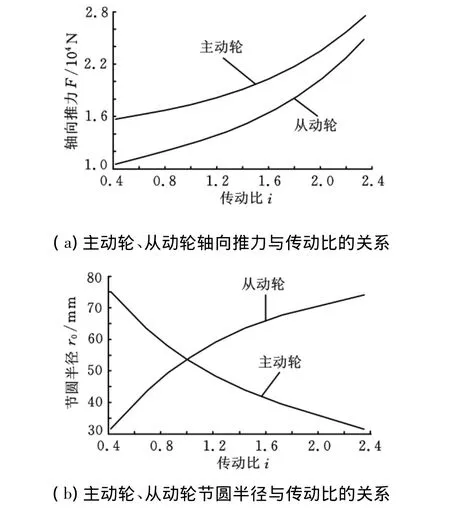
图7 主动轮、从动轮轴向推力、节圆半径与传动比的关系
切向压应变直接影响着径向位移的改变,径向位移又与钢带环的伸长量在圆弧段有一定的对应关系。与应力应变和传动比的关系相反,图8所示为主动轮和从动轮上钢带环的径向位移。随着传动比的增大,主动轮上钢带环的径向位移先减小后增大,从动轮则是一直增大。造成这一现象的主要原因是切向压应变和节圆半径的变化。当传动比i=2.35时,钢带环层间隙最大,主动轮上层间隙最大为0.03μm,从动轮上层间隙最大为0.02μm。虽然这是层间最大间隙,但其数值仍然很小,因此可以忽略。与1.2节中关于“钢带环之间既无间隙也无过盈”的假设相符。
图9所示为主动轮、从动轮包角范围内钢带环的伸长规律,由于随着传动比的增大,节圆半径和径向位移不断增大,从动轮上钢带环的伸长量也随之增大,伸长量范围是0.02~0.113mm。在主动轮上,随着传动比的增大,节圆半径的变化趋势是不断减小,径向位移是先减小后增大,且增大较多,因此,其钢带环伸长量的变化规律是先减小后增大,但增大的较少,主动轮上钢带环伸长量的变化范围为0.053~0.71mm。
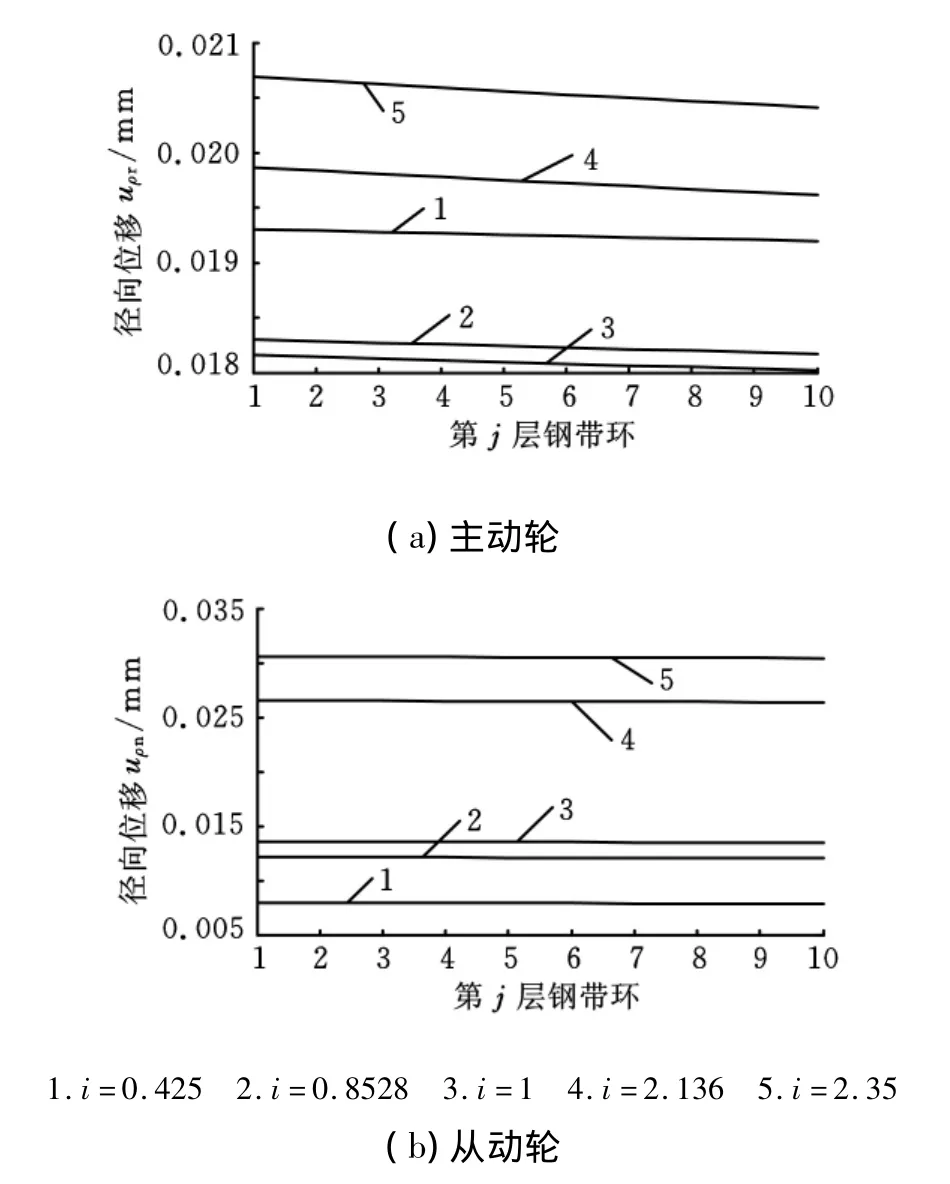
图8 钢带环径向位移
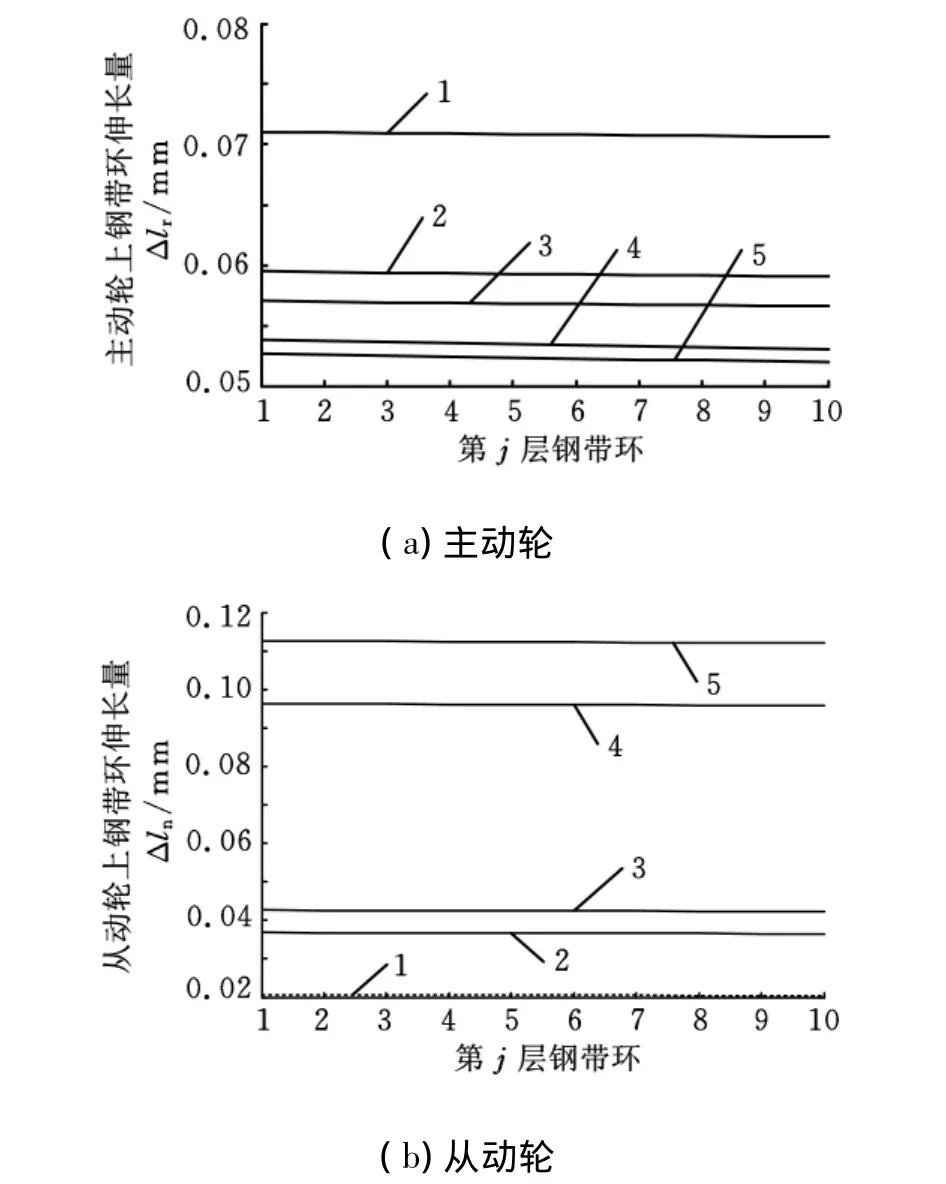
图9 主动轮、从动轮圆弧段上钢带环伸长量
图10所示为直线段上钢带环的伸长量。直线段上的钢带环被简化为单向拉伸模型,由于钢带环横截面面积不变,所以钢带环伸长量变化规律仅由钢带环拉力来决定。结果显示:bc段上钢带环的伸长量变化范围是:传动比 i<1时为0.1~0.144mm,i≥1时为0.11~0.16mm;ad段上钢带环的伸长量变化范围是:传动比i<1时为0.096~0.127mm,i≥1时为0.118~0.183mm。
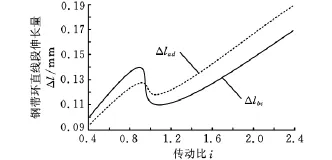
图10 直线段上钢带环的伸长量
将钢带环在直线段和圆弧段的伸长量相加,便可得钢带环总的伸长量。如图11所示:当传动比一定时,最内层钢带环的伸长量最大,最外层的最小,其最大差值为0.0013mm。变化范围是0.19%~0.25%。虽然此差值较小,但是它造成了各层钢带环受载不均匀。由于轴向推力的不断增大,钢带环的伸长量总体上随着传动比的增大而增大。但是当传动比为1时,钢带环的伸长量有所下降。究其原因是:对钢带环伸长程度有较大影响的是钢带环在直线段上的张力,但是当传动比为1时直线段上的张力减小了,因此钢带环的伸长量也有所减小。此时主动轮、从动轮节圆半径相同,金属块鞍面与最内层钢带环以及钢带环之间的相对速度为零,摩擦功率损失为零,所以此时变速器的效率在整个传动比变化过程中是最大的[10]。本研究中钢带环最小伸长量为0.2882mm,最大为 0.5136mm,线应变范围是0.04% ~0.08%,钢带环的弹性极限是1.1%。
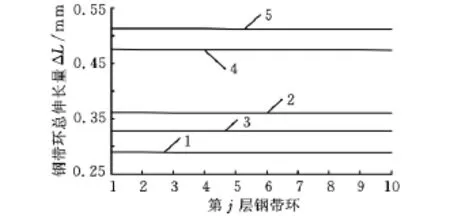
图11 各层钢带环总的伸长量
2.3 应变能损失分析与讨论
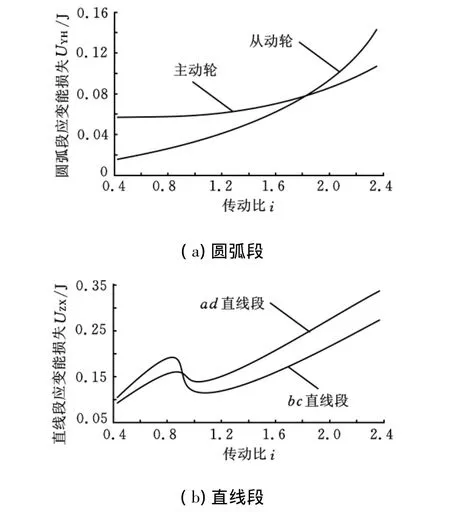
图12 钢带环应变能损失
图12a所示为主动轮、从动轮包角上钢带环的能量损失。由图可以看出,无论是主动轮还是从动轮,应变能损失都是随着传动比的增大而增大,且当传动比越来越大时,从动轮的应变能损失程度较主动轮的更剧烈。两曲线的交点不存在任何意义。图12b为直线段上钢带环的能量损失,由图可以看出,上部钢带环和下部钢带环的应变能损失都随着传动比的增大而增大。无论传动比为何值,上部钢带环和下部钢带环的长度是一样的,并且横截面面积也一样。但是,传动比不同时,主动轮、从动轮的节圆半径不一样,这样就导致了上部钢带环和下部钢带环紧边和松边属性的变换。当传动比i<1时,Tbc>Tad,bc段钢带环应变能损失较大。当传动比i≥1时,Tbc<Tad,ad段钢带环应变能损失较大。与此同时,传动比i=1还具有以下特性:由于主动轮、从动轮节圆半径相同,变速器各组件间的摩擦力瞬间降低,导致bc段和ad段钢带环张力同时下降,所以,此时钢带环应变能损失有所减小。图13所示为钢带环总应变能损失,其范围为0.3~0.9J。
3 功率损失分析与讨论
在变速器运动过程中,对于钢带环上任意一个微小的截面来讲,它都会在“主动轮圆弧段-bc直线段-从动轮圆弧段-ad直线段”上循环运行,因此,任意微段截面应变能是不断变化的。但是钢带环在任意时刻的总应变能都在图13所示的范围内。按照主动轮6000r/min的转速,应变能每秒最大变化100次。这种变化不全部是从钢带环原始长度开始的,也有可能是从某变形较小状态到某变形较大状态,或者是从某变形较大状态到某变形较小状态(这种情况下钢带环不会消耗能量,反而是在释放应变能)。
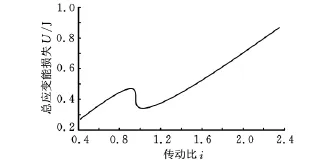
图13 钢带环总应变能损失
由式(20)可得与总应变能损失曲线(图13曲线)类似的应变能功率损失曲线,其功率损失结果如表2所示。

表2 参数及数值
钢带环应变能功率损失范围为27.15~86.73W,此数值是按变速器最恶劣的工况来计算的。当主动轮转速小于6000r/min,或者钢带环从变形较大的状态向变形较小的状态转变时,相应应变能导致的功率损失会小于以上数据。传动比为1时,总应变能损失有所下降,这从另一个方面证实了业界普遍认同的“传动比为1时变速器效率最高”这一观点。
4 结论
(1)基于弹性力学理论建立了MB-CVT钢带环伸长模型。在圆弧段上,钢带环被简化为组合薄壁圆筒模型;在直线段上,被简化为单向拉伸模型。
(2)钢带环伸长模型计算结果显示:随着传动比的增大,应力应变在主动轮上不断增大,在从动轮上先减小后增大;径向位移在主动轮上先减小后增大,在从动轮上却不断增大。当传动比一定时,无论是在主动轮还是从动轮上,最内层钢带环的应力应变和径向位移都最大,最外层的最小。
(3)钢带环总的伸长量随着传动比的增大而增大。但是当传动比为1时,由于变速器部件的摩擦功率损失下降,所以钢带环总的伸长量有所减小。钢带环最小伸长量为0.2882mm,最大为0.5136mm,线应变范围是0.04% ~0.08%。
(4)应变能损失分析结果显示:总应变能损失随着传动比的增大而增大,由于CVT各部件间的摩擦力减小,当传动比为1时总应变能损失有所减小。总功率损失范围为27.15~86.73W,当传动比为1时,总功率损失为34.85W。本研究可为金属带式CVT结构优化提供参考。
[1]Kong Lingyuan,Parker R G.Steady Mechanics of Layered,Multi-band Belt Drives Used in Continuously Variable Transmissions(CVT)[J].Mechanism and Machine Theory,2008,43(2):171-185.
[2]Kuwabara S,Fushimi Y,Fujii T,et al.Study on a Metal PushingV-beltTypeCVT:Numerical Analysis of Forces Acting on a Belt at Steady State[J].JSAE Review,1998,19(2):117-122.
[3]Kim H,Lee J.Analysis of Belt Behavior and Slip Characteristics for a Metal V -belt CVT[J].Mechanism and Machine Theory,1994,29(6):865-876.
[4]Akehurst V,Vaughan N D,Parker D A,et al.Modeling of Loss Mechanisms in a Pushing Metal V-belt Continuously Variable Transmission[J].Journal of Automotive Engineering,Part D,Proc.Inst.Mech.Eng.,2004,218:1269-1306.
[5]Sun D C.Performance Analysis of a Variable Speedratio Metal V - belt Drive[J].Journal of Mechanisms,Transmissions and Automation in Design,1988,110:472-481.
[6]Micklem J M,Longmore D K,Burrows C R.Modeling of the Steel Pushing V-belt Continuously Variable Transmission[J].Journal of Mechanical Engineering Science Part C,1994,208(1):13-27.
[7]Kuwabara S,Fujii T,Kanehara S.Study on a Metal Pushing V-belt Type CVT:Band Tension and Load Distribution in Steel Rings[J].JSAE Review,1999,20(1):55-60.
[8]Carbone G,Mangialardi L,Bonsen B,et al.CVT Dynamics:Theory and Experiments[J].Mechanism and Machine Theory,2007,42(4):409-428.
[9]张武,周春国,刘凯.金属带式无级变速器带轮变形研究[J].中国机械工程,2010,21(15):1771-1774.
[10]张武,刘凯,周春国,等.金属带式无级变速器摩擦功率损失研究[J].中国机械工程,2010,21(11):1293-1297.
