点接触摆线行星传动齿面构建方法

易文翠 陈兵奎 李海翔

1.重庆大学机械传动国家重点实验室，重庆，400030

2.重庆电子工程职业学院，重庆，401331

0 引言

摆线类行星传动具有传动比大、刚性好、结构紧凑、传动精度高等特性，在国防工业及国民经济建设的各个领域获得了广泛的应用。近年来不少学者在摆线齿轮啮合传动理论方面作了有益的工作。Livtin等［1-2］推导了摆线齿廓的共轭啮合方程，得到了齿廓的生成方法，并对齿面接触特性进行了研究。Lai等［3-5］根据曲面单参数的包络方法建立了摆线针轮传动的啮合方程，并对摆线行星轮的设计方法和加工方法进行了研究。文献［6-9］推导了移距修形、等距修形及转角修形的摆线轮齿形通用方程式。文献［10-11］根据齿轮啮合原理，建立了行星轮共轭齿廓的通用方程和锥形摆线齿廓方程，并对啮合特性进行了系统分析。上述研究中的摆线针轮共轭啮合齿面接触为线接触，线接触轮齿通常有摩擦和滑动，而滑动是齿面磨损、产生热量和功率损耗、降低效率、缩短寿命的重要因素。

本文根据齿轮啮合原理，在摆线针轮行星传动曲面共轭的基础上，研究曲面与曲线的接触问题;对点接触摆线行星传动的概念作出了定义，提出了点接触摆线行星传动的产生方法，建立了相应的几何学理论，构建了管状啮合齿面;推导了针齿啮合管齿面与摆线轮的点接触啮合副的齿面方程和接触线方程，给出了针齿啮合管的位置参数和啮合管半径的选择方法，分析讨论了点接触摆线行星传动的特性。

1 点接触摆线行星传动的形成方法

图1中，曲面Σ1和曲面Σ2分别为齿轮1和齿轮2上已知的两个相互共轭的摆线针轮齿面，曲线Γ1为曲面Σ1上选取的一条光滑曲线，曲线Γ2为曲面Σ2上与曲线Γ1相共轭的曲线。

在保持曲面Σ2不变的情况下，在曲面Σ1上选定曲线Γ1。Γ1应同时满足以下4个条件:①Γ1上任一点的主法矢方向和原齿面上同一位置点的法线方向相同;②Γ1∈Σ1，即所选曲线在曲面Σ1上;③Γ1在自变量的定义域内是关于自变量的无穷可导函数，即Γ1是一条光滑曲线;④Γ1在原共轭齿面整个啮合区都有取值。

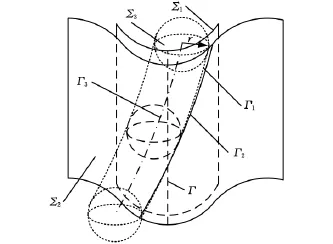
图1 摆线行星传动点接触示意图

满足上述4个条件的曲线Γ1与曲面Σ2按原给定方式运动时，可保持在各接触点连续相切接触，因此为曲线与曲面接触，故称Γ1和Σ2构成点接触啮合。

因现实中曲线不能单独存在，且不具备传递运动和动力的能力，故需构造一个新的曲面∑3，该曲面应包含曲线Γ1，且在啮合过程中只有曲线Γ1参与接触，如图1所示，即形成点接触啮合。

2 点接触摆线行星传动的基本理论

2.1 摆线针轮行星传动共轭齿廓方程

图2所示的坐标系中，在针轮与行星轮的中心分别建立与之固连的动坐标系S1(O1X1Y1Z1)和S2(O2X2Y2Z2)，在针齿中心建立动坐标系Sz(OzXzYzZz)，在针轮中心建立整体固定坐标系S(OXYZ)。在初始位置，X轴和X1轴重合，X2轴、Xz轴与X轴平行。针齿中心分布圆半径为Rz，针齿的半径为rz，针轮、行星轮的齿数分别为zb和zg，两轮中心距(输入转臂轴承的偏心距)为e。为简化问题，采用转臂(曲柄)O1O2固定法。将行星轮绕Z2轴逆时针旋转α角，根据相对运动关系，针轮将随行星轮绕Z1轴逆时针旋转β角。

根据文献［11］，可写出针齿齿廓在S1中的方程:

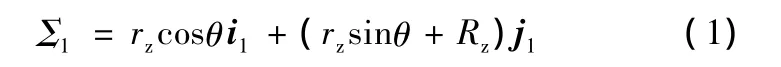
式中，θ为在任何位置均对轮齿形状无影响的角参量。

摆线轮齿廓在S2中的方程为

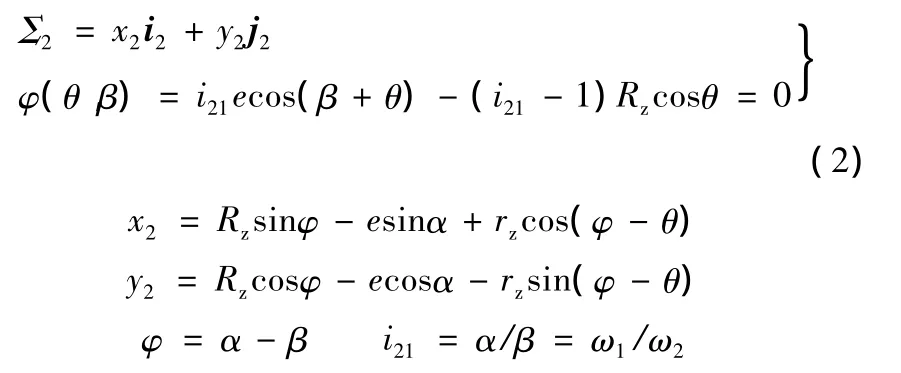
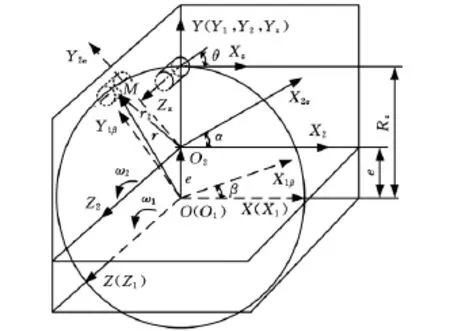
图2 固定坐标系与动坐标系

2.2 针齿面上光滑曲线的选取

为便于描述，在摆线针轮行星传动针齿齿面上选取曲线Γ1，构造新的曲面Σ3来代替针齿齿面，如图1所示。

如图3所示，按前述4个条件在针齿上选定曲线Γ1，由式(1)可得Γ1在S1坐标系中的方程:

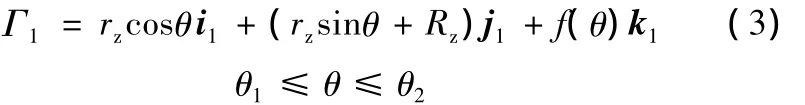
式中，θ1、θ2分别为针齿参与啮合的最小转角和最大转角;f(θ)为曲线在轴向的变化函数，f(θ)可以是螺旋线、正弦曲线、余弦曲线等。

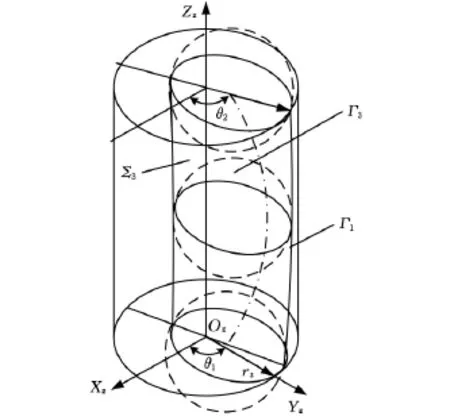
图3 针齿啮合管示意图

2.3 针齿啮合管齿面的构建

如图3所示，Γ3为Γ1的等距线，等距量为r，由式(3)可得Γ3在S1坐标系中的方程:

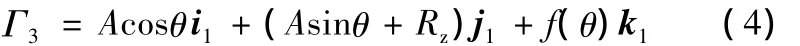
式中，A为原针齿圆柱面半径与等距量之差，A=rz－r。

根据微分几何［11］，以等距线Γ3为球心轨迹线，等距量r为半径的球族方程为

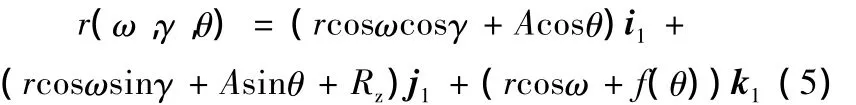
式中，ω、γ为球面参数，0≤ω≤2π，0≤γ≤2π。

根据单参数曲面族的包络理论［10］，球族包络面的啮合方程为

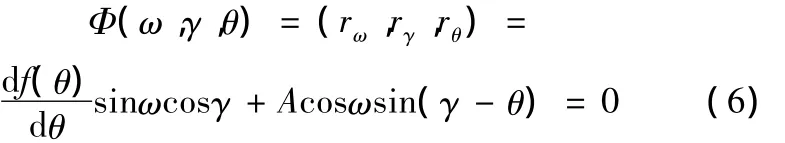
式中，rω、rγ、rθ为曲面族 r(ω，γ，θ)对参数 ω、γ、θ的偏微导。

联立式(5)、式(6)可得球族管状包络面方程Σ3在S1坐标系中的方程:

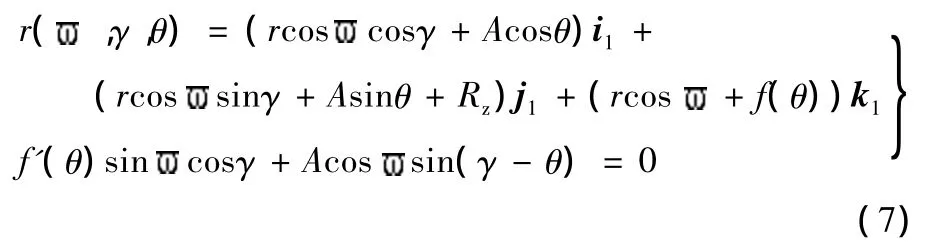
此时，球族管状包络面Σ3与原针齿面Σ1恒定相切于曲线Γ1，曲线Γ1是包络面Σ3上的一条脊线;啮合过程中，包络面Σ3上只有曲线Γ1参与啮合，即球族管状包络面Σ3与曲面Σ2构成点接触共轭啮合，将球族管状包络面Σ3称为啮合管齿面。

2.4 摆线轮上的接触线

根据齿轮啮合原理，Γ1的共轭曲线Γ2在S2中的方程为

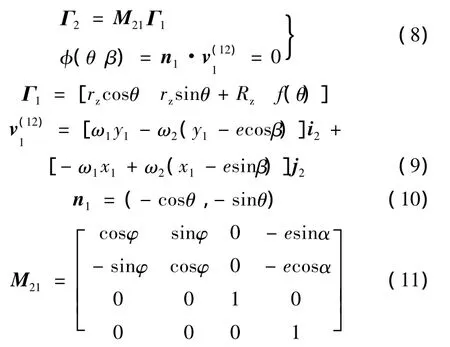
式中，M21为坐标系 O1βX1βY1βZ1β到坐标系 O2αX2αY2αZ2α的变换矩阵。

将式(9)～式(11)代入式(8)，得到Γ1在S2中的共轭曲线Γ2的方程:

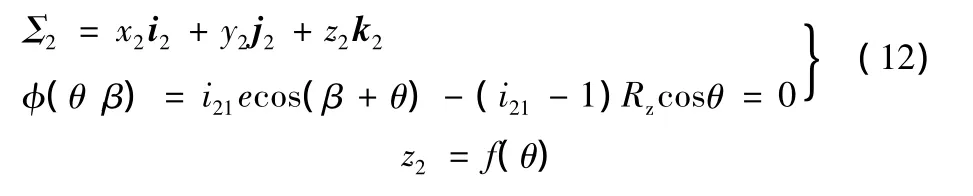
3 点接触摆线行星传动设计实例

3.1 光滑曲线的选取

圆柱螺旋线是圆柱面上的光滑曲线，且具有曲率和挠率都是常数但不为零的性质，因此将原针齿圆柱面上一条圆柱螺旋线作为曲线Γ1。此时，由式(3)可得Γ1在S1中的方程:

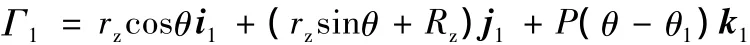
式中，P为螺旋线节距，P=B/(θ2－θ1);B为齿宽。

根据式(7)，针齿啮合管齿面在S1中的方程为

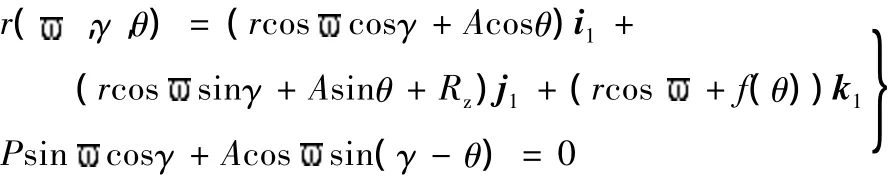
根据式(12)，摆线内齿轮上的接触线Γ2在S2方程为

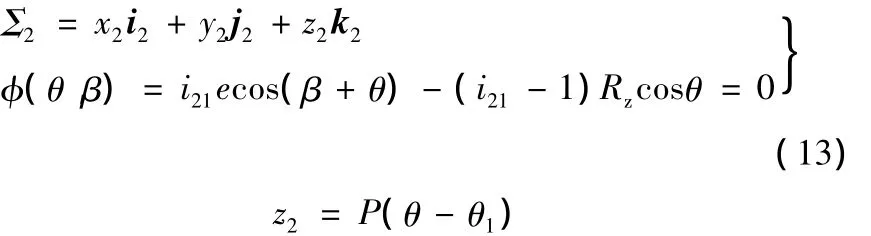
3.2 针齿啮合管齿面参数

3.2.1 位置参数

根据文献［12］可知，摆线针轮啮合时，针齿只是部分参与运动，并且摆线针轮行星运动过程中，针齿存在两次接触。如图4所示，针齿在啮合过程中只有K1K'n部分齿廓参与啮合，所以针齿始终重复着由K1转至K'n，再反向转回K1的运动。K'n处是针齿与摆线轮的凸齿、凹齿接触转换点，在K1处，针齿上的这点分别与摆线轮的凸齿、凹齿接触。用啮合管齿面代替针齿齿面后，为了不改变原来的啮合特性，将螺旋线Γ1的起点选择在K1点，终点选择在Kn点，Kn在端面上的投影为K'n。那么在啮合过程中，啮合管齿面就重复着K1→Kn→K1的转动，在端面上就是K1→K'n→K1的转动。这样可继承原摆线针轮行星传动的啮合特性。

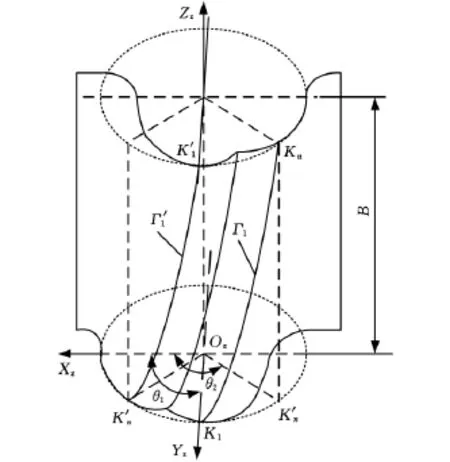
图4 针齿啮合管齿面示意图

本例将K1点放在Yz轴上，则此时θ1=π/2，θ2可以根据文献［12］中的公式计算出来。因传动过程有正反转，在针齿的另一侧按上述方法选择一条Γ1的等距线Γ'1就是针齿反转接触线。

3.2.2 啮合管半径

为保证啮合管齿面Σ3上只有曲线Γ2参与啮合，啮合管半径必须满足r＜rz。同时，为保证用啮合管齿面代替原针齿齿面时啮合特性改变量较小，啮合管的半径r又不能取太小。图4为针齿啮合管齿面单齿齿形示意图。

3.3 点接触摆线行星传动特性分析

将式(2)和式(13)进行比较可知，两式中的x坐标、y坐标的表达式相同，因此针齿上给定的光滑曲线Γ1的共轭曲线Γ2在摆线轮上，并且该曲线沿Z轴方向按P(θ－θ1)变化，是一条摆线柱面螺线。

啮合副中的摆线轮齿廓没有任何的变化，只是用啮合管齿面代替了原来的针齿齿廓。啮合管齿面和针齿圆柱面相切于曲线Γ1处，Γ1为啮合管齿面上的一条脊线，如图4所示，其余各点的曲率半径小于原针齿半径，所以在啮合过程中均不与摆线齿面接触，即啮合管齿面上只有曲线Γ1参与啮合，从而具有点接触的性质。

啮合管齿面和摆线轮齿面的端面投影与传统的摆线针轮行星传动相同。如图4所示，啮合管齿面上的接触曲线就是原针齿上的一条曲线，由前述曲线的选取条件可知，这条曲线在整个针齿啮合区域内都有取值，因此点接触的摆线行星传动可继承传统摆线针轮行星传动的啮合齿数多、重合度大、啮入啮出平稳、误差平均效应显著等优点。

3.4 实体模型

本文所研究的点接触摆线针轮行星传动装置，是在针齿上选择一条圆柱螺旋线为光滑曲线构造啮合管齿面，以啮合管齿面为针轮新齿面同摆线轮相啮合。点接触摆线行星传动基本参数如表1所示。

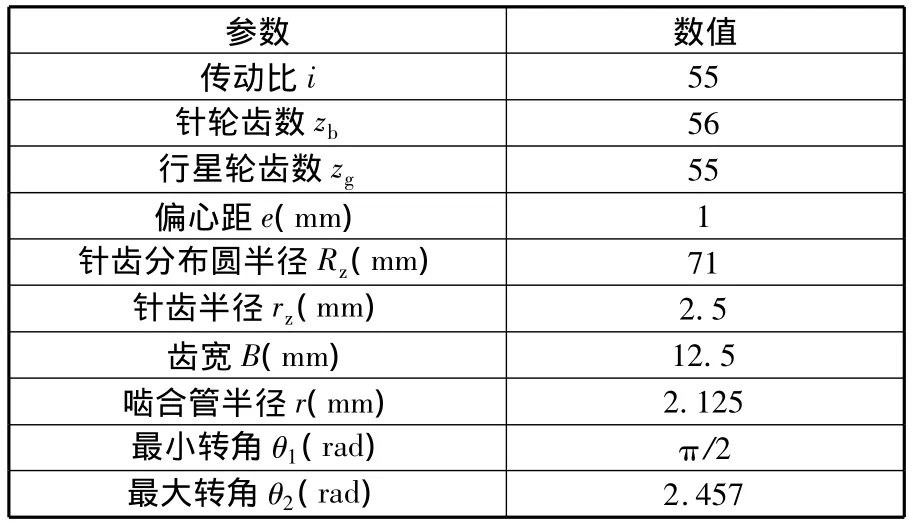
表1 点接触摆线行星传动参数表

根据表1中点接触摆线行星传动的几何参数，利用三维建模软件创建内齿轮三维实体模型(图5)，其啮合管齿面实体模型如图6所示。

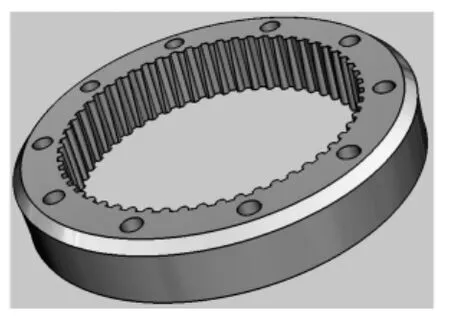
图5 针轮实体模型

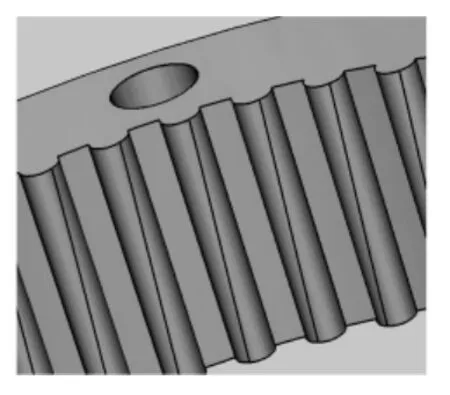
图6 啮合管齿面模型

4 结论

(1)提出了点接触摆线行星传动的定义，并给出由摆线针轮共轭啮合副齿面形成点接触共轭啮合的一般方法。

(2)推导了点接触摆线行星传动的啮合管齿面方程及与其共轭的齿面接触线方程。

(3)以摆线行星传动为基础，在针齿上选择一条圆柱螺旋线为光滑曲线来构造针齿啮合管齿面，以啮合管齿面同摆线轮齿面相啮合所形成的点接触摆线行星传动为设计实例，确定其转角参数和啮合管半径，讨论了点接触摆线行星传动的特性。

(4)给出了点接触摆线行星传动装置的设计参数，构建了针轮及啮合管齿面实体模型。

［1］Ltivin F L，Fuentes A.Gear Geometry and Applied Theory［M］.New York:Cambridge University Press，2004.

［2］Ltivin F L，Feng P H.Computerized Design and Generation of Cycloidal Gearings［J］.Mechanism and Machine Theory，1996，31(7):891-911.

［3］Lai T S.Design and Machining of the Epicycloid Planet Gear of Cycloid Drives［J］.International Journal of Advanced Manufacturing Technology，2006，28(7/8):665-670.

［4］Lai T S.Geometric Design of Roller Drives with Cylindrical Meshing Elements［J］.Mechanism and Machine Theory，2005，40(1):55-67.

［5］Yan H S，Lai T S.Geometry Design of an Elementary Planetary Gear Train with Cylindrical Tooth－profiles［J］.Mechanism and Machine Theory，2002，37(8):757-767.

［6］李力行.摆线针轮行星传动的齿形修正及受力分析［J］.大连铁道学院学报，1984(4):40-49.

［7］李力行，洪淳赫.摆线针轮行星传动中摆线轮齿形通用方程式的研究［J］.大连铁道学院学报，1992，13(1):7-122.

［8］关天民.摆线针轮行星传动中摆线轮最佳修型量的确定方法［J］.中国机械工程，2002，13(10):811-813.

［9］鲍君华，何卫东，卢琦，等.针轮输出摆线针轮行星传动研究［J］.中国机械工程，2010，21(19):2339-2344.

［10］陈兵奎，蒋旭君，王淑妍.新型锥形摆线轮行星传动初步研究［J］.现代制造工程，2005(2):14-15.

［11］李瑰贤.空间几何建模及工程应用［M］.北京:高等教育出版社，2007.

［12］Chen B K，Fang T T，Li C Y.Gear Geometry of Cycloid Drives［J］.Science in China Series E:Technological Sciences，2008，51(5):598-610.