叶轮流道非正交四轴加工的刀轴控制方法

吴宝海 韩飞燕 杨建华 秦 涛

1.西北工业大学现代设计与集成制造技术教育部重点实验室，西安，710072

2.西安航空发动机(集团)有限公司，西安，710021

0 引言

自由曲面叶轮广泛应用于航空、航天等领域，它工作转速高、形状复杂、加工精度高，而叶轮流道型面的加工精度对整机性能有着重要的影响。目前国内外自由曲面叶轮大多采用五轴联动的加工方式进行加工［1］，但五轴机床价格昂贵，而且我国许多叶轮生产厂家仍有大量四轴设备，从加工成本和生产实际情况考虑，研究叶轮的四轴数控加工方法对于开发现有设备的加工潜力、降低叶轮加工成本有着重要的现实意义。

在流道加工中，由于刀具伸入叶轮长度最大，同时还要避免刀具与叶片压力面和吸力面的干涉，因此，流道加工的刀轴控制是自由曲面叶轮加工中最为关键的内容。与五轴加工中刀轴为一自由矢量相比，四轴加工的刀轴被约束在其摆刀平面上，因此，叶轮流道四轴加工中刀轴控制更加困难，刀轴控制直接决定了叶轮四轴加工的可能性、加工质量和效率。许多学者针对自由曲面［2-4］的刀轴控制方法开展了大量研究，而针对自由曲面叶轮流道加工刀轴控制方法的研究甚少。文献［5］通过对流道两侧叶片压力面和吸力面相应的精加工刀轴矢量进行线性插值得到流道粗加工的刀轴矢量，但该方法无法保证刀轴在整个流道加工切削轨迹上光滑过渡。文献［6］提出了一种新的侧刃铣削五轴加工叶轮流道刀轨生成算法，该算法通过设置刀轴矢量变化的阈值并采用集合碰撞体，实现了刀轴的全局碰撞快速检查，但该方法并未涉及干涉后刀轴的修正问题。文献［7］借鉴动画制作中设置关键帧的思想，提出了一种新的全局过渡光滑的刀轴矢量生成方法，该方法需要在干涉位置重复插入关键刀轴来修正干涉，降低了算法速度。上述刀轴控制方法仅适用于五轴加工，对于四轴加工，文献［8-9］开展了相关研究，但都是基于曲面的局部信息，计算出每一个切触点处无干涉的刀轴，没有考虑相邻刀轴矢量之间的光滑过渡问题。文献［8］在一组锥形面矢量组中，求取与由曲面局部信息计算出的刀轴矢量最相近的矢量作为最终刀轴，该方法可能会出现修正后仍无法避免干涉的刀轴。文献［9］利用两个圆锥面求交集并结合叶轮加工的特点给出了非正交四轴加工刀轴矢量的确定方法，该方法的缺点是初始后跟角的取值对算法收敛性影响较大。

本文针对自由曲面叶轮流道非正交四轴加工的刀轴控制，提出在约束刀轴的单位圆锥面上，由流道两侧相应的清根刀轴来旋转插值流道加工的刀轴矢量的方法。

1 非正交四轴加工刀轴约束面的建立

在自由曲面叶轮的四轴加工中，为了增加叶轮的加工开敞性、减小刀具深入流道的长度以降低碰撞干涉发生的可能性，需将工作台倾斜一定的角度，使四轴机床成为非正交四轴机床，如图1所示。

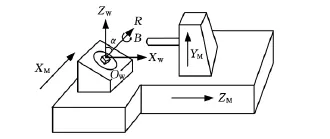
图1 带倾斜回转工作台的四轴加工示意图

图1中，机床的平动坐标轴为 XM、YM、ZM，旋转运动为绕工作台回转轴线的转动。工作台绕XM轴旋转角度α后，工作台的回转轴线变为R轴，不再与机床的平动坐标轴重合。在刀具轨迹规划中，工作台的旋转可看作是刀轴绕回转轴R的摆动，因此，刀轴矢量不再被约束在常规四轴加工的摆刀平面内，而是被约束在以回转轴 R为轴，π/2－α为半顶角的圆锥面上，所以满足该四轴机床约束条件的所有刀轴就位于一系列回转轴线平行于R，半顶角为π/2－α的圆锥面上。研究该非正交四轴加工的核心问题即是如何在这一系列圆锥面上确定合适的刀轴矢量以实现对给定曲面的加工。

基于此，在工件坐标系下建立以原点OW为顶点，回转轴线R为轴，π/2－α为半顶角的单位圆锥作为刀轴约束面，如图2所示，使满足约束条件的刀轴矢量经过平移后都位于该单位圆锥面上，从而将四轴机床加工的核心问题转化为如何在单位圆锥面上确定合适刀轴的问题。

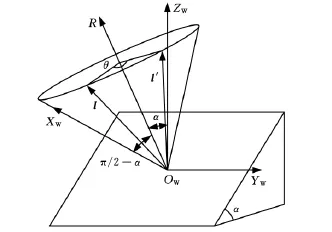
图2 单位圆锥母线绕回转轴旋转示意图

在工件坐标系OWXWYWZW中，回转轴线R的初始矢量为(0，0，1)，绕YW轴旋转角度α后回转轴矢量R的表达式为

单位圆锥面S的表达式为

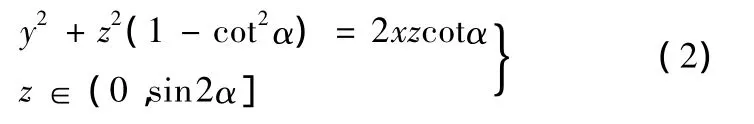
2 清根刀轴的确定

从几何构造的角度考虑，离心叶轮流道是由叶片叶根曲线绕轴线旋转一周得到的曲面，因此，流道加工的轨迹分布及刀轴也可由清根轨迹及刀轴通过插值的方式获得。本文首先计算清根切触点的初始刀轴，然后将初始刀轴向单位圆锥面投影，再将投影矢量在圆锥表面上旋转修正来计算各个切触点处无干涉的清根刀轴。

2.1 清根初始刀轴的计算

在流道加工中，初始刀轴的选取应尽量保证实际加工中刀具深入流道的长度最短，且在切削轨迹上尽量均匀变化。根据上述原则，清根初始刀轴的确定如图3所示。假设清根切触轨迹C1已知，C1i为C1上第i个切触点，L为叶片压力面Sp的叶顶线，在流道进出口位置，为了保证仍能得到合适的初始刀轴，将L沿其切向延长一段距离，按照点到曲线的距离计算出垂足pc，连接垂足pc与切触点C1i作为初始刀轴。本文定义切触点C1i处的初始刀轴为l0i=pc－ C1i，l01、l0n分别为流道进出口切触点处的初始刀轴矢量。

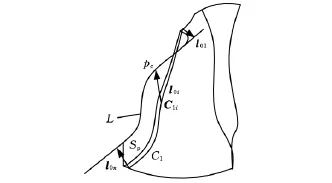
图3 初始刀轴示意图

2.2 无干涉清根刀轴的计算

流道清根初始刀轴可能不满足非正交四轴加工的刀轴约束条件，即不在刀轴约束面上，因此，需将初始刀轴平移至单位圆锥顶点后向圆锥表面S投影，并在圆锥面上进行碰撞干涉的检测与修正，使投影后的初始刀轴满足刀轴约束条件且无干涉。初始刀轴平移至圆锥顶点时会出现三种情况:第一种是平移后的矢量l0在圆锥外部(图4a);第二种是平移后的矢量l0在圆锥内部(图4b);第三种是平移后的矢量在圆锥表面S上，这种情况不需计算。下面计算平移后的初始刀轴在圆锥内部和外部时向圆锥表面投影后得到的刀轴矢量。

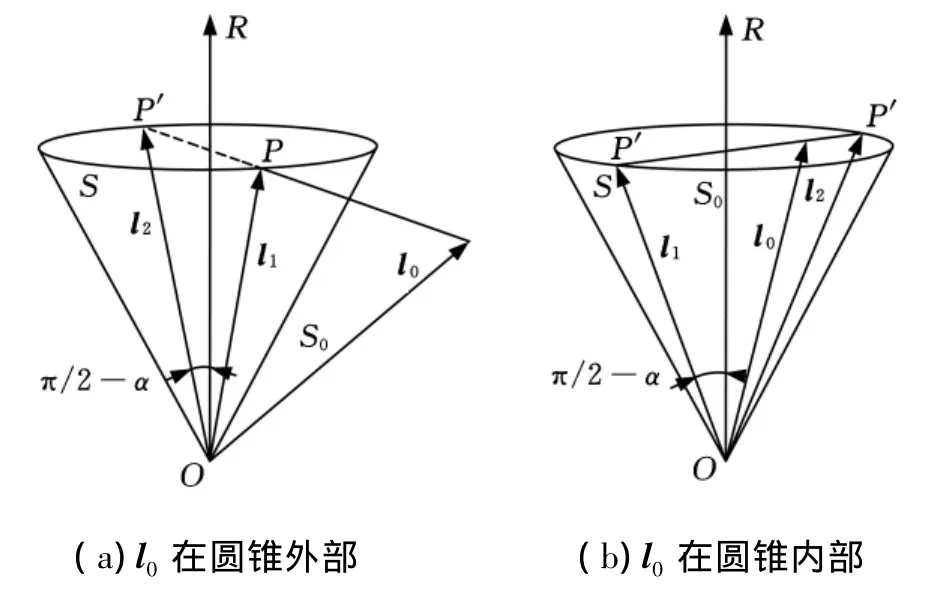
图4 初始刀轴投影示意图

由几何学知识可知，矢量l0在单位圆锥面S上投影的刀轴矢量即为过矢量l0与回转轴R构成的平面S0与单位圆锥面S的交线OP与OP'。由解析几何知识可知:

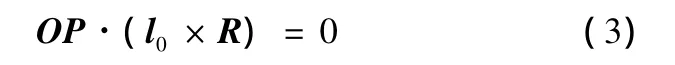
且P点为单位圆锥圆周上的点，因此

假设OP 为(x，y，z)，矢量 l0为(l0x，l0y，l0z)，那么联立式(2)～式(4)，得

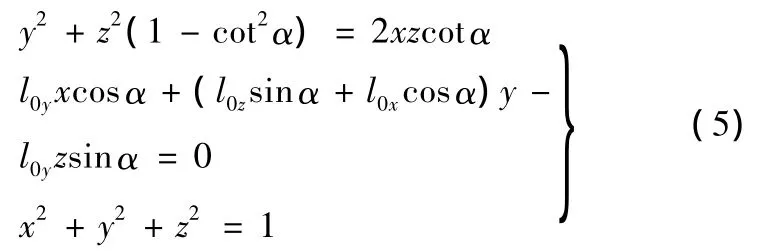
其中，l0、α 已知，且 z∈ (0，sin2α)，由式(5)可求出两个刀轴矢量(x1，y1，z1)和(x2，y2，z2)，记为l1、l2。如图4所示，这种情况下得到两个刀轴矢量l1和l2在数学上均满足四轴加工的条件，而在实际加工中只有一个刀轴矢量是合理的，文献［9］给出了如何在l1、l2中选取合理的刀轴矢量的判断方法。

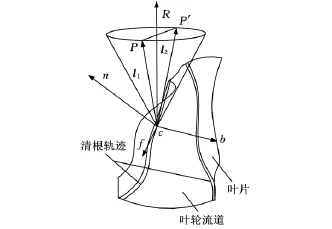
图5 合理刀轴矢量的选取

选取的合理刀轴矢量虽满足刀轴约束条件，但仍可能会与流道两侧叶片发生碰撞干涉，因此需对其进行干涉检查及修正。干涉检查可采用基于距离监视的方法［10］，而刀轴的修正可通过调整刀轴在单位圆锥面上的位置来实现(如图5所示，若选取的合理刀轴矢量l1发生干涉，可以将l1绕单位圆锥回转轴R朝向远离干涉曲面的方向旋转一个合适的角度)。

3 流道加工刀轴的确定

在叶轮流道两侧清根刀轴确定的情况下，流道加工刀轴的计算可采用矢量插值的方法。为满足非正交四轴机床的刀轴约束条件，本文采用在刀轴约束面上旋转插值清根刀轴矢量的方法来计算流道加工刀轴矢量，并采用机床运动学优化方法对流道加工同一个切削行上的刀轴进行了光顺处理。

3.1 流道清根切触轨迹的对应处理

采用本文方法计算流道加工的刀轴时，首先要保证流道两侧清根轨迹上的切触点数目是相等的，且序列号相同的切触点应该在同一个流道周向回转圆周上，这样两条清根轨迹上的切触点才是一一对应的，才能使插值后的周向刀轴在同一个回转圆周上连续变化。而在流道加工中，由于流道曲面不是规则曲面，因此流道两侧清根轨迹线上切触点数目可能不相同。按照切触点序列依次旋转插值流道周向刀轴时，序列号相同的切触点在流道曲面上的位置就可能不在同一个圆周上，而在数控加工中，不同切触点处的刀轴矢量是不同的。在这种情况下，需对清根轨迹上的切触点进行对应处理，使清根轨迹具有相同的切触点数目，且序列号相同的切触点位于同一个回转圆周上。

假设流道清根切触轨迹分别为C1、C2，在C1、C2中选取切触点较多的那条作为基准线，并计算与之一一对应的另一条清根切触轨迹。若C1为基准线，延长C2。计算C1上某一点C1i到叶轮回转轴R 的距离为 di，建立 di、nt、C2、R 与曲线 C2对应的参数ui的映射关系:

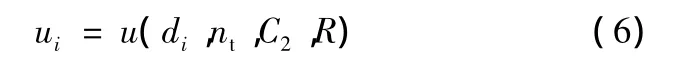
其中，nt是C2的切触点数目，R是叶轮回转轴。得到ui后可以在C2中找到一个与C1i具有相同回转半径di的切触点C2i，依次重新计算出一条与C1一一对应的清根轨迹C2，如图6所示。则由对应处理后的C1、C2计算的清根刀轴，经过旋转插值后得到的流道周向刀轴是在同一个流道回转圆周上连续变化的。

图6 对应清根轨迹计算示意图

3.2 旋转插值方法

为满足非正交四轴机床的刀轴约束条件，可采用旋转插值的方法根据清跟刀轴和流道加工轨迹线确定流道加工的刀轴分布。旋转插值方法的原理是将刀轴矢量绕单位圆锥回转轴R沿插值方向旋转，插值区域是清根刀轴在圆锥面上确定的扇形曲面区域，旋转插值的方向和角度根据清根轨迹上对应切触点处的刀轴矢量在单位圆锥面上的位置来计算。因此，旋转插值方法可以保证插值后的矢量都位于刀轴约束面上，且均匀变化。

由上述方法计算出的清根刀轴矢量满足刀轴约束条件，平移到单位圆锥顶点后仍位于圆锥表面上，相当于一条圆锥母线。平移后的刀轴绕圆锥回转轴R的旋转过程，可看作矢量绕过原点的空间任意轴线的旋转过程。如图2所示，根据计算机图形学中的旋转变换方法，矢量l绕R轴旋转θ角后的矢量为

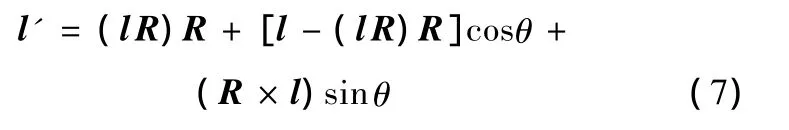
这种插值方法不仅保证了流道加工的刀轴矢量位于非正交四轴机床的刀轴控制面上，而且能保证插值后的刀轴完全位于流道压力面、吸力面清根刀轴所围成的空间内。因此，只要流道两侧清根刀轴无干涉，就能保证插值获得的流道加工刀轴不会与相邻叶片发生碰撞干涉，从而避免了对流道加工刀具碰撞干涉的检查及修正。

3.3 旋转角度及插值方向的确定

如图 7 所示，Ti，1、Ti，n分别为流道两侧清根轨迹C1、Cn上第i个切触点对应的清根刀轴，M、N分别为 Ti，1、Ti，n与单位圆锥圆周线的交点。清根刀轴Ti，1与Ti，n在单位圆锥面S上确定的曲面区域为S1，曲面S1在圆锥圆周线上对应的曲线段为MN，MN在圆锥顶面上确定了一个圆心角θi，θi就是 Ti，1和 Ti，n在圆锥上确定的圆心角，也就是清根刀轴 Ti，1和Ti，n之间旋转插值的总角度。

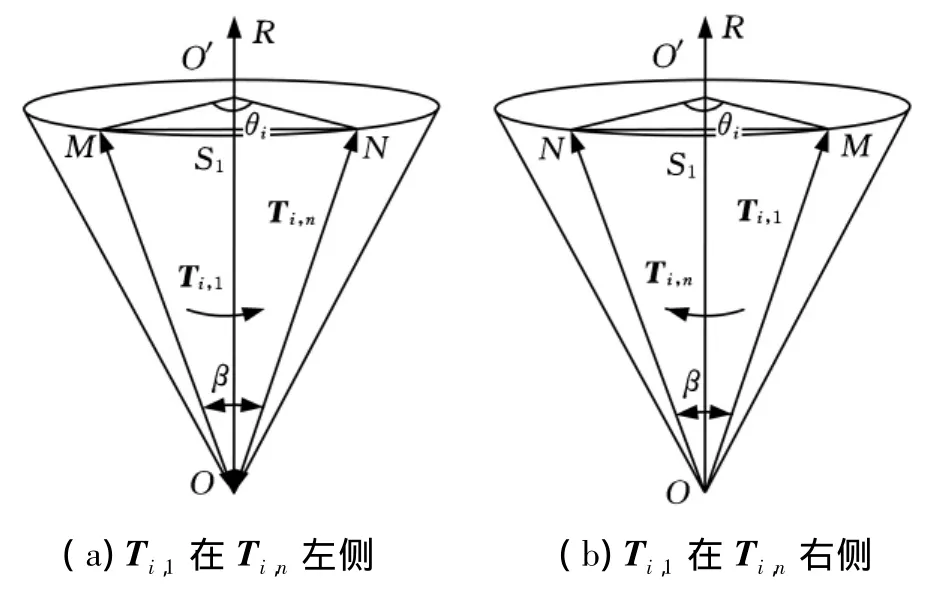
图7 插值方向示意图

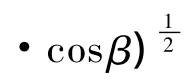
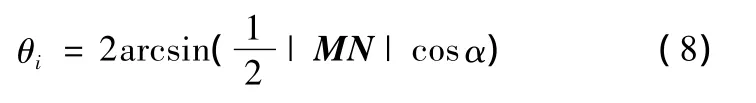
第i行第j列的叶轮周向刀轴Ti，j对应的旋转插值角度为

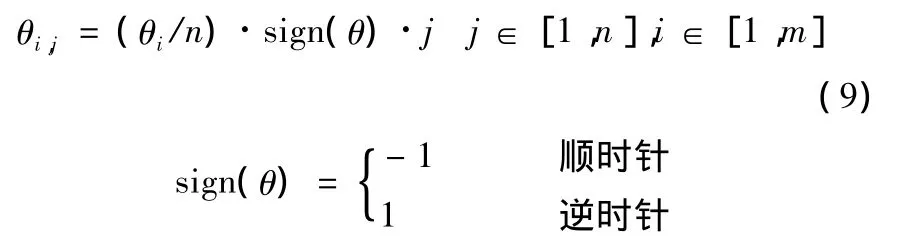
其中，sign(θ)是与刀轴旋转方向有关的系数，n是流道加工切削行数目，m是一条切削行轨迹上的切触点数目。

在叶轮流道加工中，本文定义清根刀轴Ti，1、Ti，n之间的插值方向为由 Ti，1变换到 Ti，n时的旋转方向。因此，如果(Ti，1× Ti，n)·R ＞ 0，说明 Ti，1在 Ti，n左侧(图 7a)，插值方向为由 Ti，1逆时针旋转到 Ti，n;如果(Ti，1× Ti，n)·R ＜ 0，说明 Ti，1在Ti，n右侧(图 7b)，插值方向为由 Ti，1顺时针旋转到 Ti，n。

因此，在确定旋转角度及插值方向后，流道第i 行第 j列的刀轴矢量 Ti，j可以由 Ti，1、Ti，n、θi，j代入式(10)来计算。由于流道周向的旋转插值角度θi，j是均匀变化的，所以对应切触点处的刀轴旋转插值后得到的周向刀轴矢量 Ti，j也是连续变化的。

3.4 流道加工切削行内相邻刀轴的光顺

采用上述方法计算的刀轴矢量，只能保证在每一个切触点处流道周向刀轴是无干涉且连续变化的，而不能保证同一个切削行内相邻刀轴矢量之间是光滑过渡的。因此，需要对同一个切削行内的刀轴再进行光顺处理。

对于图1所示非正交四轴机床，刀轴只有一个绕回转轴R的转动自由度，当刀轴绕R相对初始刀轴位置(如图1所示，在该四轴机床中，初始刀轴位置为主轴位置(0，0，1)，其在工件坐标系下为(1，0，0))转动θ后，就与初始刀轴在约束刀轴的圆锥上确定一个圆心角θ，因此对相邻刀轴的光顺可以通过约束相邻刀轴之间的圆心角来实现，即

其中，δθ表示刀具由切触点Ci运动到切触点Ci+1时，刀轴由Ti(θi)变换到Ti+1(θi+1)的转动速度，λθ为图1所示机床工作台转动时的速度约束值，vi为当前切触点的进给速度，本文中假定加工时刀具的进给速度恒定。

4 算例分析

为验证本文方法的正确性与有效性，以图8所示自由曲面叶轮为研究对象进行了验证。该叶轮高度为 250mm，内径为 372mm，外径为1130mm，具有22个等长叶片，流道最窄处宽度为49.775mm，叶片型面为空间扭曲自由曲面且最大高度为275mm。与直纹面三元叶轮相比，自由曲面叶轮沿叶片高度方向扭曲更为严重，且在叶片压力面侧存在内凹现象，导致刀轴控制更加困难。

图9、图10分别为采用本文方法生成的清根轨迹与流道一条切削轨迹上的刀轴分布图，图11所示为流道周向插值的刀轴分布。由图9～图11可知，本文方法获得的流道加工切削行轨迹上的刀轴及其周向插值的刀轴都是连续变化的。

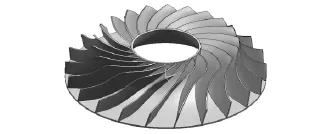
图8 叶轮示意图

图9 流道清根刀轴示意图

图10 流道一条切削轨迹刀轴示意图

图11 流道周向刀轴示意图

对于非正交四轴加工来说，每个切触点处的刀轴矢量唯一对应一个绕单位圆锥回转轴的旋转角度。如果切削行轨迹上刀轴矢量是平滑变化的，那么它绕回转轴的旋转角度应该是连续变化的。由此可知，流道加工中刀轴对应的旋转角度在一个切削行内是连续变化的。在非正交四轴机床实际加工过程中，刀轴矢量绕回转轴R的旋转是通过机床工作台的旋转来完成的。相邻刀轴矢量之间旋转角度的增量变化情况会影响机床工作台转动的平稳性。在一个切削行轨迹上刀轴的旋转角度连续变化并不能说明相邻刀轴的旋转角度就不会产生剧烈变化。

图12、图13分别为清根刀轴和流道一条切削轨迹上相邻刀轴之间的旋转角度增量变化图。由图可知，这两条切削行轨迹上相邻刀轴对应的旋转角度最大变化量分别为3.512°和1.569°。由此可见，流道切削行轨迹上相邻刀轴的旋转角度无剧烈变化，这意味着在流道加工过程中机床工作台的转动较为平稳，在一定程度上确保了机床运行的稳定性，从而保证了加工的精度。

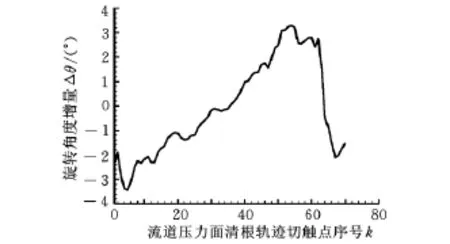
图12 流道压力面清根刀轴旋转角度增量变化图

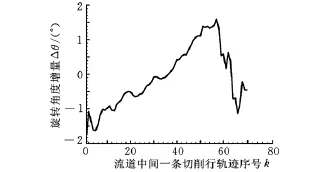
图13 流道一条切削轨迹上刀轴旋转角度增量变化图

本文方法适用于流道开敞性相对较好的自由曲面、直纹面类型的三元离心叶轮的加工，包括长叶片和长短叶片两种形式。对于流道开敞性较差的离心叶轮，可通过旋转工作台倾斜角度的优化和调整实现其四轴加工，也可通过增加分度机构进一步增强四轴机床加工离心叶轮的能力。对于叶片稠度大且扭曲严重的离心叶轮，仍然需要五轴联动加工设备进行加工。

5 结论

(1)依据非正交四轴机床特性，建立满足刀轴约束条件的单位圆锥，在该单位圆锥面上旋转插值刀轴的控制方法简单易行。

(2)本文通过对一个等长叶片形式的自由曲面叶轮流道加工的刀轴控制进行具体计算，算例分析结果表明，本文方法可以获得叶轮流道非正交四轴加工既无干涉又较为均匀变化的刀轴矢量，并且能够保证加工过程中机床的运行较为平稳。

(3)本文方法可以准确、有效地解决等长叶片形式的自由曲面叶轮流道非正交四轴加工中刀轴矢量的控制问题，同样也适用于长短叶片形式的自由曲面叶轮加工。与五轴加工相比，本文方法更具实用性和经济性。

(4)通过对工作台倾斜角度的优化选取，可以进一步发掘四轴机床加工自由曲面叶轮的能力。

［1］Tsay D M，Chen H C，Her M J.A Study on Five－ flank Machining of Centrifugal Compressor Impellers［J］.Journal of Engineering for Gas Turbines and Power，2002，124(1):177-181.

［2］Lu J，Cheatham R，Jensen C G，et al.A Three － dimensional Configuration－space Method for 5－axis Tessellated Surface Machining［J］.International Journal of Computer Integrated Manufacturing，2008，21(5):550-680.

［3］Luo Ming，Zhang Dinghua，Wu Baohai，et al.ToolOrientation Control Using Quaternion Interpolation in Multi－ axis Milling of Blade［C］//International Conference on Manufacturing Automation.Hong Kong，2010，128-132.

［4］Balasubramaniam M，Sarma S E，Marciniak K.Collision－ free Finishing Toolpaths from Visibility Data［J］.Computer－ Aided Design，2003，35(4):359-374.

［5］陈良骥，王永章.整体叶轮五轴侧铣数控加工方法的研究［J］.计算机集成制造技术，2007，13(1):141-146.

［6］孙全平，廖文和.叶轮曲面5轴高速铣加工刀轨生成算法［J］.东南大学学报，2005，35(3):386-390.

［7］姬俊锋，周来水，安鲁陵，等.一类开式整体叶轮五坐标数控加工刀轴矢量生成及其光顺方法的研究［J］.中国机械工程，2009，20(2):79-83.

［8］蔡永林，查建中，孙卫青.叶轮四坐标数控加工中刀轴矢量的计算［J］.推进技术，2004，25(2):88-91.

［9］吴宝海，王尚锦.自由曲面叶轮的四坐标数控加工研究［J］.航空学报，2007，28(4):993-998.

［10］南长峰，吴宝海，张定华.复杂通道类零件五坐标加工全局干涉处理方法［J］.航空学报，2010，31(10):2103-2108.