基于小波分析的漏钢预报温度数据处理

张本国 李 强 王 葛 孙丽凤 张志克

1.燕山大学，秦皇岛，066004 2.河北科技大学，石家庄，050018

3.邯郸钢铁集团公司，邯郸，056015

0 引言

漏钢是连铸过程中最具危害性的事故。开发实时、准确的漏钢预报系统，对漏钢趋势提前预警，是防止漏钢事故发生的主要手段［1-2］。热电偶测温法凭借其极强的实时性与可操作性成为目前普遍采用的漏钢预报方法［3-4］。热电偶测温法的预报原理是依靠结晶器铜板内所埋设的热电偶测得温度，实时地对铸坯表面状况进行监测，热电偶测温实质上是一种动态温度波形的模式识别问题，即从热电偶监测的温度波形中识别出具有漏钢征兆的波形。

由于连铸现场工况复杂，干扰很多，热电偶所采集的温度数据中不可避免地存在一定的噪声信号及异常值，而这些噪声及异常值的存在严重制约着漏钢预报系统的准确度。笔者在对连铸现场所采集的大量温度数据做了详细分析后，把小波分析理论引入到板坯连铸漏钢预报系统中，对温度信号进行噪声消除处理，在很大程度上提高了系统的反应速度及预报准确度。

1 小波分析降噪原理

由于在正交小波中，正交基的选择比传统方法更接近实际信号本身，所以通过小波变换可以更容易地分离出噪声或其他不需要的信息，因此小波分析在信号降噪中有着传统方法无可比拟的优势［5-7］。

一般情况下，所采集的信号s(n)由目标信号f(n)和噪声e(n)组成:

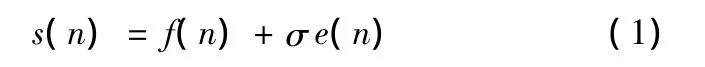
式中，n为信号长度;σ为噪声强度。

小波变换的目的就是要抑制e(n)以恢复f(n)。采用

小波分析进行信号降噪的过程如图1所示。

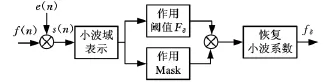
图1 小波分析信号降噪过程

图1中，Fδ为阈值算子，作用阈值算子后，模值小的系数被置为零，模值大的系数项被保留，即

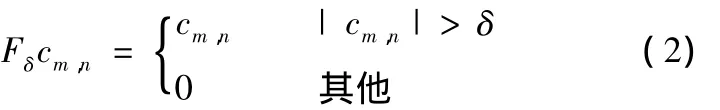
式中，cm，n、Fδcm，n分别为阈值处理前后的小波系数值;δ为设定参数。

Mask为掩码算子，其作用是保留特定系数并把其他系数置零，即

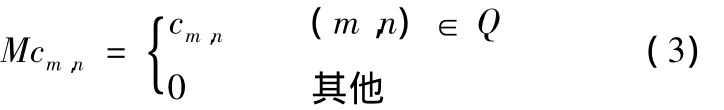
式中，Mcm，n为阈值处理后的小波系数值;Q为系数条件。

掩码算子是阈值算子的推广，可以通过引入系数模值的掩码算子来实现阈值算子。

由图1可以看出，采用小波分析进行信号降噪的过程可分为以下3个步骤:

(1)小波分解。用选定的小波函数对信号进行N层小波分解。

(2)作用阈值。为小波分解的各层系数选择阈值，并对各层系数作相应的阈值处理。

(3)信号重建。将阈值处理后的系数通过小波重建得到降噪后的目标信号。

在小波分解系数上作用阈值，是小波分析用于信号降噪过程中最为核心的步骤。将信号进行多层小波分解后，通过对各层分解系数做相应的阈值处理来抑制信号中的噪声成分，从而达到信号降噪的目的。

2 小波分析在漏钢预报中的应用

2.1 数据前处理

热电偶实时采集的温度数据是一组动态的时间序列，为了将这组动态数据转化为静态数据，本文采用了延时网络技术(TDNN)，见图2。

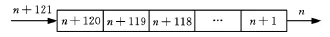
图2 TDNN示意图

在仿真程序中，先定义一个移位寄存器，将单个热电偶所采集的时间序列温度数据输入该寄存器，形成一个“先进先出，后进后出”的队列。利用该寄存器便可以从动态的时间序列温度数据中截取相应长度的静态温度数据序列。

通过对某板坯连铸厂漏钢温度记录进行分析，发现典型的漏钢事故发生前热电偶所测温度的波动过程所需时间约为25s;为包含温度波动的整个过程，取单个热电偶温度波动模式识别的时间为30s，热电偶的采样间隔为0.25s。文中给出了一组粘结漏钢发生前30s所监测的温度波形，见图3。

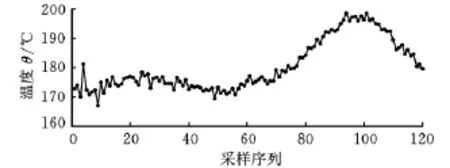
图3 粘结漏钢温度样本序列

由图3可以看出，连铸现场所采集的温度信号中包含了高频的噪声信号和低频的目标信号。

2.2 温度信号的小波分解

笔者用多种小波分解方法做了尝试，通过分析比较分解结果，最终选择了db3小波函数对温度信号进行5尺度小波分解，分解结果如图4所示。

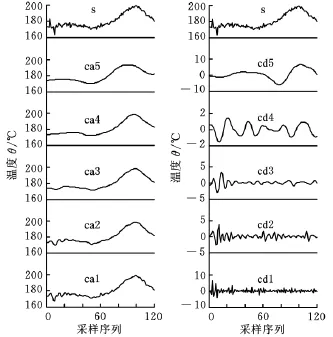
图4 温度信号的5尺度小波分解

从图4可以看出，前4层的细节系数幅值范围多在4℃内;在分解到第5层时，细节系数的幅值发生了很大变化，高达20℃，近似部分也变得过于平滑，降低了对温度变化趋势的描述。因此在对温度信号做多尺度小波分解时，只分解到第4层。

2.3 各级阈值的确定

在各层小波分解系数上作用阈值是应用小波分析进行信号降噪过程中最为关键的步骤，阈值的选取结果会直接影响到信号的降噪效果。在小波变换中，各层系数降噪所需的阈值一般是根据原信号的信噪比，即式(1)中的σ来选取的。从s(n)中提取σ的方法有多种，本文选用原信号各层小波分解系数的标准差来对噪声强度进行估计。

虽然目前存在几种阈值确定理论及其对应的经验模型，但是这些理论或模型都有一定的局限性和使用范围，没有一种阈值确定模型是可以通用的。因此，本文分别采用缺省阈值确定模型、Birge－Massart策略确定的阈值模型和小波包变换中的Penalty阈值模型对小波系数进行处理，并将各阈值作用结果进行比较。

(1)缺省的阈值确定模型为

式中，λ为阈值。

(2)Birge－Massart策略确定的阈值可以通过以下规则求得。

给定一个分解层数j，对于j+1以及更高层，所有系数保留;对于第i层(1≤i≤j)，保留系数绝对值较大的ni个系数，ni的表达式为

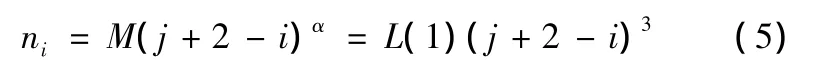
其中，M和α为经验系数，降噪情况下取α=3;M满足L(1)≤M≤2L(1)，L(1)为第一层小波分解后的系数长度。

(3)小波包变换中的Penalty阈值确定。

假设当分解层数t为满足条件的特定值t*时，函数

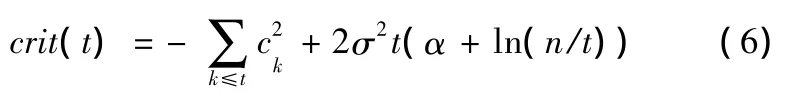
式中，ck为小波包分解系数中第k大的系数。

取得最小值，则阈值:

2.4 温度信号的小波重建

分别采用以上3种阈值确定模型确定小波分解各级系数的阈值，并分别将其作用在各层系数上，最后进行温度信号的小波重建。通过分别作用不同阈值得到的降噪结果，如图5所示。

图5 小波重建结果

通过以上3种阈值模型所获得的目标信号的能量均占原信号能量的90%以上。从图5可以看出，Penalty阈值和Birge－Massart阈值降噪结果比较理想，而缺省阈值降噪结果在第0～10个采样点之间存在较大的局部跳动，有悖于信号降噪的光滑性准则，进而排除了缺省阈值降噪方法。Penalty阈值和Birge－Massart阈值降噪结果与原信号的标准差分别为19.87和17.51;因为信号降噪的相似性准则是降噪后的信号和原信号的方差估计应该是最坏情况下的最小值，所以Birge－Massart阈值降噪结果是最好的。

因此，在将小波分析降噪方法应用于漏钢预报系统进行温度数据处理过程中选用了Birge－Massart阈值确定方法。

3 结语

文中采用db3小波函数，对热电偶所采集的温度数据进行4尺度的小波分解，然后采用Birge－Massart阈值对小波分解系数进行处理，最后重建温度信号，去除了温度信号中由于现场干扰所引起的噪声。去除噪声后的温度信号包含了原信号96%的能量，并且符合信号降噪的光滑性及相似性准则，能够更好地反应出热电偶所采集温度的变化趋势，为漏钢特征的识别提供了更为准确的数据。

［1］何涛焘，田陆，黎锋果，等.基于热电偶测温的漏钢预报系统［J］.传感器世界，2010(11):29-33.

［2］Lee D，Moon C H，Moon S C，et al.Development of Healing Control Technology for Reducing Breakout in Thin Slab Casters［J］.Control Engineering Practice，2009，17(1):3-13.

［3］蔡娥，许军，白居冰，等.漏钢预报新技术研发及应用［J］.钢铁研究，2009，37(4):29-32.

［4］秦旭，朱超甫，高光河，等.板坯漏钢机理及基于热电偶检测的漏钢预报技术研究［J］.钢铁研究学报，2011，23(2):7-11.

［5］袁昌茂，文鸿雁.变形监测数据处理的小波去噪方法［J］.地理空间信息，2009，7(4):136-138.

［6］唐桂文，江恒彪，左建章.基于小波阈值去噪理论的监测数据处理方法［J］.测绘科学，2009，34(1):117-118.

［7］Tang Guiwen，Jiang Hengbiao，Zuo Jianzhang.Application of the Theory of Wavelet Analysis and the Distribution of Noise on the Monitoring Data of Project［J］.Science of Surveying and Mapping，2009，34(1):117-118.