高可靠性工控设备寿命验证试验的方案设计
2012-12-01翁思健
翁思健 何 斌
(上海工业自动化仪表研究院,上海 200233)
0 引言
随着现代工业生产规模的日益扩大,对控制系统的可靠性也提出了严苛的要求。如果系统中某个部件频繁出现故障,不但会影响控制系统的正常运行,还会进一步影响到工业生产的正常进行,造成巨大的损失。近年来,国内外自动化设备生产厂商日益重视高可靠性设备的研发项目。
据预测,最新推出的一些产品的平均无故障工作时间(mean time between failure,MTBF)可以达到百万小时水平。如果依然采用传统方法验证这些高可靠性设备的MTBF,并希望试验数据的置信度维持在较高水平,那么试验周期、样本数量就会大大增加,从而超出设备生产厂商的承受能力。为此,针对这些产品,迫切需要一套具有高度可操作性的MTBF验证方案。本文将传统的MTBF验证方法与加速寿命方法相结合,设计了一套针对高可靠性工控设备的寿命验证方案。与传统方案相比,该方案具有试验周期短、样本数量少等优点,且试验数据的置信度水平不会因此而降低。
1 可靠性相关理论
1.1 产品寿命分布
一台设备的可靠性往往能够通过以下5个函数得到较好的描述,即失效率密度函数、可靠性函数、有条件的可靠性函数、失效率函数和平均寿命函数。表1显示了这些函数的符号、定义以及相互关系。
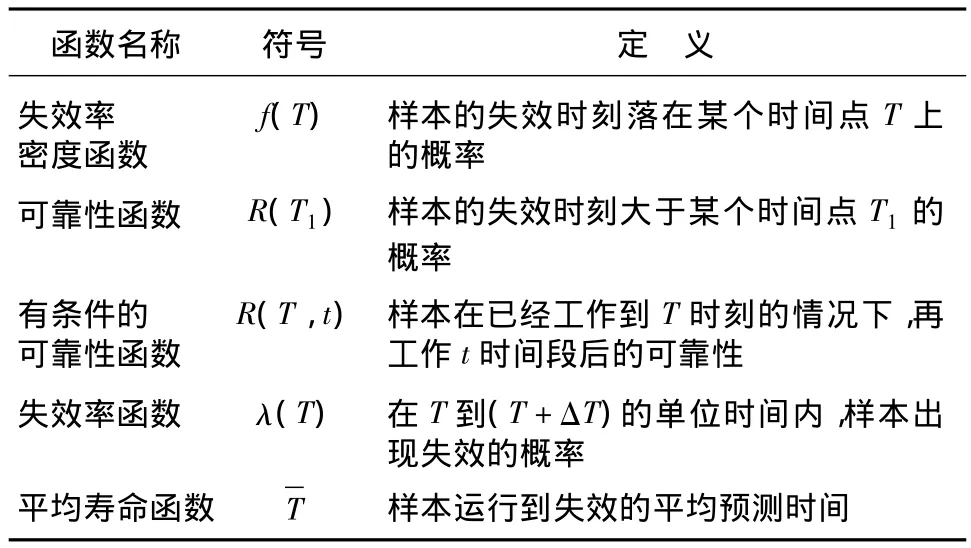
表1 可靠性和寿命试验函数Tab.1 The functions in reliability and lifespan test
研究表明,大多数设备(包括电子产品)的失效率与产品生命周期之间满足Weibull分布,其失效率密度函数和失效率函数如式(1)、式(2)所示[1]。式中:β、η为常数;t为工作时间。如果用作图法表示,可以得到一条两头高、中间低的曲线,称之为“浴盆曲线”,如图1所示。
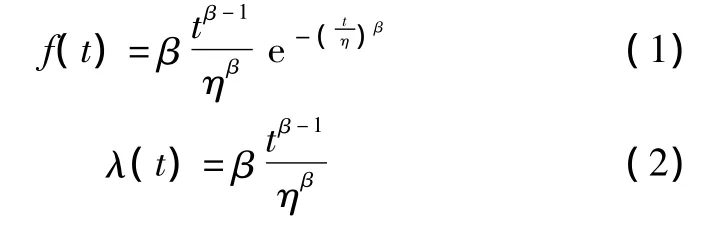

图1 浴盆曲线Fig.1 Bathtub curve
由图1可以看出,产品的生命周期可以被划分为3个阶段,即早期失效阶段、随机失效阶段和疲劳失效阶段。在早期失效阶段,λ(t)随工作时间t的增加而减小,对应β<1的情况。在随机失效阶段,λ(t)基本是一个与工作时间无关的常数,对应β=1的情况。疲劳失效阶段,λ(t)随工作时间的增加而增加,对应β>1的情况。值得关注的是,当β=1时,Weibull分布将会退化为指数分布,式(1)、式(2)则简化为式(3)、式(4)[2]。

指数分布的特点是失效率函数和平均寿命函数均为常数,且两者互为倒数。因此,如果能够假设某个产品只工作在随机失效阶段,就可以用指数分布描述该产品的可靠性。
1.2 可靠性及寿命试验的类型
依据不同的分类原则,可靠性试验可划分成各种类型,不同类型的试验有各自的针对性和目的。根据试验的终止条件,可靠性试验分为失效样本固定型和时间固定型试验。根据试验过程中对失效样本的处理方式,可靠性试验分为失效样本及时替换和不及时替换型试验。同时,还可以根据参与试验的样本数量,将试验分为大批量样本试验和小批量样本试验[3]。大批量样本试验和小批量样本试验的区别在于通过前者能够直接观察到样本的失效率满足的分布形式,而通过后者无法直接看出。
1.3 试验过程及结论的表述形式
在进行可靠性试验之前,应先确定试验类型、样本数量以及样本所满足的失效率分布形式。试验过程中,需要记录的数据包括开始和终止时间、失效样本数目以及失效时刻等。
可靠性试验的结论通常以置信度(confidence level,CL)和置信区间的形式表示。置信度的定义是个体样本的某个参数值落在总体样本该参数统计值附近某一区间内的概率,该区间就是置信区间。如平均无故障工作时间(MTBF)的置信度为某个样本的寿命落在总体样本MTBF附近某一区间(置信区间)内的概率。通过试验验证,得到的MTBF一般采用以下3种表述形式[2]。
第一种是双侧置信区间形式,表达式如式(5)所示。
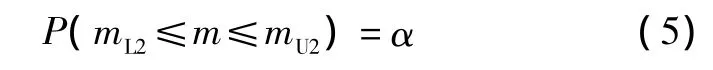
式中:m为MTBF;mL2和mU2为置信区间的下限和上限;α为置信度。这种表述形式的含义是在置信度为α的情况下,样本MTBF的置信区间为[mL2,mU2]。
第二种是低单侧置信区间形式,表达式如式(6)所示。

式中:mL1为置信区间的下限。这种表述形式的含义是在置信度为α的情况下,样本MTBF的置信区间为[mL1,∞]。
第三种是高单侧置信区间形式,表达式如式(7)所示。
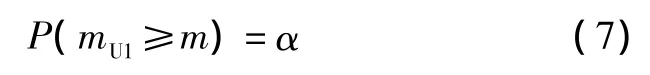
式中:mU1为置信区间的上限。这种表述形式的含义是在置信度为α的情况下,样本MTBF的置信区间为[∞,mU1]。
当样本的失效率满足指数分布时,MTBF的置信区间大小一方面与置信度、试验累计时间、失效样本数量等因素有关,另一方面与试验的类型有关。当试验类型为时间确定型且失效样本不被替换时,低单侧置信区间门限mL1的表达式如式(8)所示。
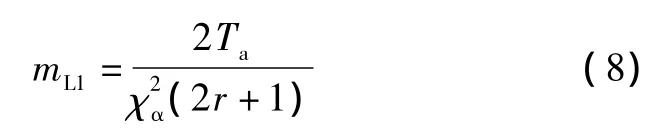
式中:mL1为置信区间的下限;Ta为累计试验时间;r为失效样本数量;α为置信度;χ2为卡方分布函数。不同参数所对应的函数值可以通过查表方法获得。值得注意的是,如果整个试验过程中没有出现样本失效,那么最终的结论只能以低单侧置信区间的形式表示。
在做小批量样本试验时,还可以通过式(9)~式(11)简单计算MTBF的估计值[3]。
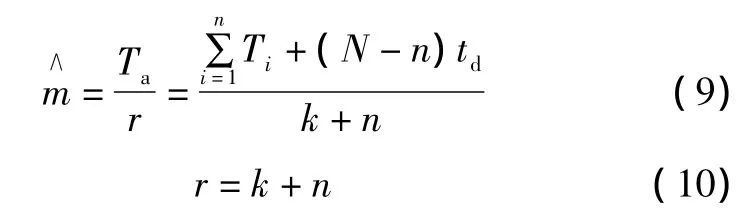
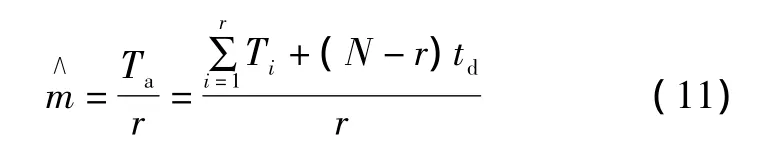
式中:td为试验结束时间;N为试验开始时的样本数;r为试验结束时总失效样本数;k为失效并且被替换的样本数;n为失效但没有被替换的样本数;Ti为这n个样本各自对应的失效时刻。式(11)适用于试验过程中失效样本不被替换的情况。
2 加速寿命验证试验
加速寿命验证试验是一种能够快速获得/验证被测产品可靠性数据的方法。该方法通过对受试样本施加一项或多项强度超过正常应力范围的加速应力来缩短样本的平均无故障工作时间(MTBF),从而达到加速样本使用寿命的目的[4-5]。加速环境下的可靠性数据乘以加速因子(AF)(正常应力下的寿命与加速应力下的寿命之比),就能够得出该产品在常规使用环境下的可靠性数据。与不施加加速应力的常规寿命验证试验相比,加速寿命试验能够缩短试验时间、节省试验花费。
加速寿命试验的关键在于选择合适的加速应力源、加速应力强度并确定相应的加速因子。相关研究人员经过大量试验,已总结出多种加速寿命模型,其中较为常用的有Arrhenius模型、Inverse Power Law模型和 Combination 模型等[6]。
Arrhenius模型适用于指数分布、加速应力为温度且高于设备的正常工作温度的情况,其加速因子表达式如式(12)所示。

式中:AF为加速因子;mU为样本在正常应力下的寿命;mA为样本在加速应力下的寿命;T*U为正常使用时的温度(绝对温度);T*A为加速温度(绝对温度);B为常数。
Inverse Power Law模型适用于Weibull分布、加速应力为非热能应力的情况,其加速因子表达式如式(13)所示。

式中:VU为正常使用时的非热能应力;VA为非热能加速应力;n为常数。
Combination模型将Arrhenius模型与Inverse Power Law模型相结合,适用于指数分布、一个温度应力与一个非热能应力同时作为加速应力的情况,其加速因子表达式如式(14)所示。

对工控设备而言,可能的加速应力源有温度、温度循环、湿度、振动应力和电应力等[7]。由于这些设备基本都是由多种类型的元器件和部件综合构成的,设备中任何一个或一类组件失效都可能导致整体失效,因此,在加速应力选择上,必须确保不超出设备中所有组件的工作极限,避免设备开始工作后短时间内即失效,超出所选模型的适用情况。
3 寿命验证试验方案设计
依据可靠性与寿命分布的相关理论,可以设计出一套采用加速寿命方法验证高可靠性工控设备MTBF的方案。该方案的目标是验证MTBF预测值超过百万小时的工控设备的可靠性。方案中假设设备的失效率满足指数形式,并要求试验结论的置信度达到90%。试验采用时间确定型与失效样本数量确定型相结合、小批量样本与大批量样本相结合的形式,试验过程中的失效样本均不作替换。参与试验的设备样本总数拟定为200台左右,试验总时间拟定为2000~5000 h。试验过程中的加速应力首选热应力(温度),在条件允许的情况下可以采用热应力与另一个非热能应力(振动、电应力等)复合的形式,以便达到较好的加速效果,对应的加速模型为Arrhenius和Combination模型。
试验分两个阶段进行,第一阶段的主要目标是确定不同应力强度对样本所产生的加速因子。
试验过程中,首先将10个样本放置在加速应力环境下,应力强度以阶梯形式逐步向上提升,直至某个强度下样本在短时间内即出现失效为止。这一应力强度就是试验样本的工作极限。试验过程中必须保证施加的应力强度低于样本工作极限。如果同时采用两种及以上的加速应力,那么具体操作时,每次只提升一种应力的强度,其他应力保持不变,直至出现失效。当各种应力相互之间的关联不明显时,可以认为样本的工作极限就是这些应力在单独变化时所能达到的最大值的叠加。
接着,在工作极限以下选取若干个加速应力点,分别对10个样本作加速试验。如果同时将两种加速应力作用于样本,那么为了给下一步的数据拟合提供便利,加速应力点的选择应参考样本MTBF估计值表。条件允许时,应尽量选择比较大的应力强度,以缩短试验时间。试验过程中,记录各个样品的失效时刻Ti,若观察到3台样本(可根据实际情况作调整)失效,则立刻中止试验。试验结束后,利用式(11)估计样本的MTBF),并将数据填写到相应的位置。

表2 不同强度加速应力下的样本MTBF估计值Tab.2 The evaluated MTBF of samples under different accelerating stress level
试验第二阶段的目标是在合适的加速应力条件下,验证样本的可靠性(MTBF)是否达到了预期水平。这一阶段试验的样本数量拟定为100台,试验类型为时间确定型。试验过程中,仍然需要记录每台失效设备的失效时间。试验结束后,可以利用式(8)计算试验样本MTBF的低单侧置信区间门限,从而验证设备的MTBF是否达到预测水平。
举例而言,假设受试设备MTBF预测值为1000000 h,试验环境产生的加速因子为100(AF=100),试验所要求的置信水平为90%(α=90%),试验时间为1000 h,试验过程中不对失效样本进行替换。在式(8)中,mL1等于MTBF预测时间除以加速因子(10000 h),累计试验时间Ta等于试验时间乘以样本数量(100000 h),由此可得(2r+1)=20。当 α=90%时,查表可得r≈6。这一结论表示,如果在1000 h的试验时间内失效样本数量≤6台,那么能够证明受试设备的MTBF>1000000 h;反之,如果失效样本数量>6台,那么无法证明MTBF达到了1000000 h。出现后一种情况时,可以考虑更改试验条件再次进行验证试验。
目前,本方案已经用于验证一款金属电容式压力/差压变送器的MTBF。试验过程按照上述设计方案执行,采用高温作为加速应力,试验结果显示这款变送器的MTBF能够达到1000000 h。
4 结束语
本文提供了一种验证工控设备平均无故障工作时间(MTBF)的试验方案。该方案将传统的MTBF验证试验方法与加速寿命方法相结合。当设备的MTBF较大时(>1000000 h),该方案能够在花费较少时间和较少样本数量的情况下,依然得到置信度水平较高的试验数据,是一种能够较准确验证产品MTBF实际水平的可行方案。该方案不仅适用于工控设备,在验证其他类型的电子、机械设备的可靠性方面同样具有参考借鉴价值。
[1]IEC.IEC 61649 Weibull analysis[S].International Electrotechnical Commission,2008.
[2]IEC.IEC 60605-4 Equipment reliability testing-Part4:Statistical procedures for exponential distribution-point estimates,confidence intervals,prediction intervals and tolerance intervals[S].International Electrotechnical Commission,2001.
[3]Kececioglu D.Reliability and life testing handbook volume 1[M].Englewood Cliffs,New Jersey:PTR Prentice Hall,1993:133 -150.
[4]Kececioglu D.Reliability and life testing handbook volume 2[M].Englewood Cliffs,New Jersey:PTR Prentice Hall,1993:605 -660.
[5]张政.浅谈加速寿命试验[J].机械,2003,30(s1):135 -136.
[6]Caruso H.A fundamental overview of accelerated-testing analytic models[C]∥ Proceedings of Reliability and Maintainability Symposium,1998:389 -393.
[7]温熙森,陈循,张春华,等.可靠性强化试验理论与应用[M].北京:科学出版社,2007:4-6.
