非参数回归算法在短时交通流预测中的应用
2012-12-01梁秀霞胡姗姗李伟斌
梁秀霞 胡姗姗 李伟斌
(河北工业大学控制科学与工程学院,天津 300130)
0 引言
随着社会经济的发展,城市化、汽车化速度加快,交通拥挤、交通事故频发、能源短缺等问题越来越突出[1]。智能交通系统(intelligent transportation system,ITS)被视为解决交通拥堵问题的重要手段[2]。它的广泛应用能够帮助人们理性地选择出行路线,能够更有效地减少环境污染,避免交通拥挤,大大减少了出行时间。
道路交通系统是一个有人参与的、时变的、复杂的非线性大系统,其显著特点是具有高度的不确定性[3]。如果我们能准确地预测出未来交通状态,就能防止交通阻塞和其他消极因素的影响。为此,本文首先研究了基于K近邻的非参数回归算法。同时,为了进一步提高算法预测的精度,从两方面对原有的算法进行了改进。首先采用主成分分析方法选取状态向量,不仅达到了降维的目的,而且体现了变量之间的综合作用;然后增加闭环回路,使模式匹配过程增加预测误差因素,使匹配过程更趋向合理。
1 算法
1.1 算法框架
为了研究交通流量Y的变化规律,通常寻找一种回归表达式Y=f(x)+u,其中x为相关变量,u为随机误差项[4],但是要找到一个固定的f(x)不容易。在非参数估计中,不需要假定这个函数f(x)的形式,也不需要设定参数。非参数估计是一种数据驱动的启发式预测机制,通过搜索历史数据库中与当前观测值相似的数据来预测未来值,它的数学模型是从历史数据中得到的。通常非参数估计可以划分为三部分:历史数据、搜索机制和预测函数[5]。
首先我们需要足够的历史数据,历史数据越多,越能完整地反应交通状况,越有利于准确地预报。然后通过主成分分析得到的状态向量和距离度量准则,在历史数据库中进行搜索,寻找K个近邻与实时数据进行匹配。最终带入预测函数中,得到下一个时刻的交通流量预测值,同时考虑误差来调节参数。
1.2 历史数据库的生成
历史数据库也可称为源范例库,预测效果的好坏直接取决于历史数据库的完整性[6]。随着交通信息采集技术的发展,信息采集范围越来越广,信息采集精度越来越高,使得获取足够高质量的历史数据成为可能。数据越完整,包含的交通流状态越多,越能够找到最接近的近邻,得到的预测效果越好[7]。然而数据量过大不利于K近邻寻找,且耗费时间过长,所以要精简冗余的数据。本文采用聚类算法,找到聚类中心和K个近邻作为代表点,提高了搜索速度。
1.3 状态向量的定义与选择
在交通领域上,状态向量是指与研究路段当前时刻流量相关联的影响因素组成的向量,影响流量的因素很多,如车辆速度、天气情况、道路状况、上下游的交通流量等都会影响本路段下一时刻流量。传统的非参数回归方法运用相关系数法,由相关系数的大小从N个变量中选择出几个比较重要的因素。但是相关系数法得到的是单个变量与被测变量直接的相关系数,而没有考虑变量之间的组合关系,这是相关系数法最大的缺点。
本文将采用主成分分析法进行状态向量的选取,它体现了变量之间的综合作用。对于短时流量预测,压缩之后的因素就是各种影响流量因素的线性组合。本文采用社会科学统计软件包(statistical package for the social sciences,SPSS)进行主成分分析。
1.4 距离度量准则
距离度量衡量了实时数据与样本数据的匹配程度。这里采用加权的欧氏距离来度量,即实时数据状态向量中各分量和历史数据库中对应点差的平分和。由于数据进行了主成分分析和聚类,所以这里的权值定义为各个主成分的贡献率。
假设当前欲匹配的模式向量为X=(V1,V2,…,VL),它与数据库中点 Pi=(V1i,V2i,…,VLi)的距离为d( X,P)i,采用加权的欧氏距离,计算公式如下。

1.5 数据匹配—K近邻法则
K近邻搜索是利用已经建立好的状态向量和相似性准则,在历史数据中找到与当前变量值相匹配的K个最近邻[8],将这K个数据代入预测函数中,可得到下一个时刻的预测值。
K值的选取一般取决于样本数据库,不同的数据库K值不同。当为特殊日期(如1月1日、5月1日等)时,K=1最为合理,因为多余的值只会减弱交通流状态本身的不确定性。由于样本数据容量问题,在此省略对特殊日期的考虑。在其余时间里,通过选取不同的K值,得到预测平均绝对误差,从而获得最优值。
1.6 预测函数
由上述近邻机制,在历史数据中找到K个近邻,实际数据与这K个近邻的距离为di(i=1,…,K),那么下一时刻流量V(t+1)可采用带权重的预测算法计算,如式(2)所示。
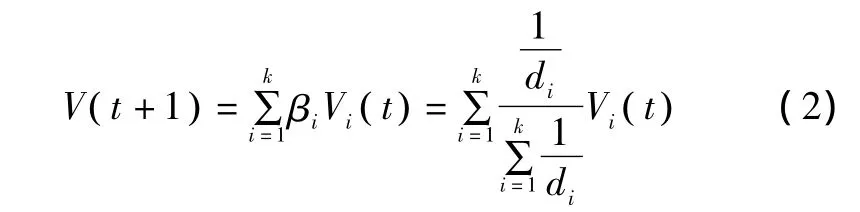
1.7 闭环反馈机制
由于状态向量中变量的不同系数影响了X与数据库里各点的距离,因此本文增加一个反馈环节,由误差e和距离来调节状态向量中变量的系数。调节公式如下。其中i表示第i个变量点,al为数据向量中第l个变量的权值,l=1,2,…,L。

2 试验结果分析
2.1 数据来源
本文对单点交通流数据进行分析,采用的交通流数据来自北京市某公路。以5 min为单位时间间隔输出2009年4月6日到2009年4月26日每天该路段的交通流量。交通流量是道路交通状况的最主要指标,因此,本文将预测下一时刻的交通流量,其中,前5472组数据用来训练,后289组数据用来测试。
2.2 试验设计
2.2.1 状态向量的选择
与预测变量相关的变量有速度、流量和占有率,每个变量保存(t-2)~t个历史数据,变量个数为9个。运用SPSS统计软件得到各主成分的特征值贡献率和累计贡献率[9],如表1 所示。

表1 主成分分析结果Tab.1 Results of principal component analysis
由表1可知,第1个特征值贡献率最高,从第3个特征值开始以后的取值都小于1。因此,选择前两个特征值。每个主成分所对应的各变量系数如表2所示。
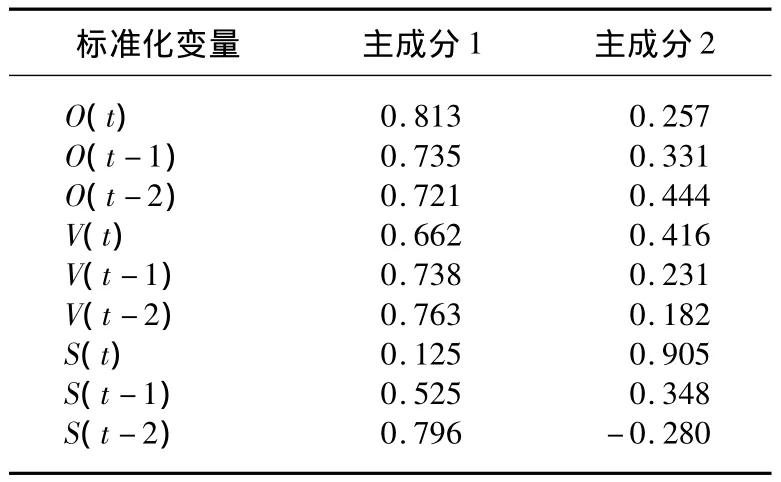
表2 主成分分析所对应的各变量系数Tab.2 Corresponding variable coefficients of principal component analysis
2.2.2 K的选取
在状态向量和预测算法都已经确定的情况下,K值的选取对预测结果很重要,K值一般从1到15。逐渐增加K值,观察K值对平均绝对误差的影响,如图1所示。

图1 K值对预测精度的影响Fig.1 Influerence of the value of K on forcasting accuracy
从图1可以看出,当K值从1增加到5时,预测精度大幅度增加;当K值从5增加到9时,预测精度逐渐降低;当K继续增加时,误差增大。因此,本文选K=9最为合适。
2.3 预测结果
本文将K个近邻值代入预测函数(2)中,得到下一时刻的预测流量,并采用Matlab进行仿真[10],得到的仿真结果如图2所示。

图2 实际交通流量与预测流量比较Fig.2 Comparison of actual traffic flow and forecasting flow
2.4 试验分析
试验结果的好坏可以由误差指标来衡量。误差指标包括平均绝对误差(MAE)、平均相对误差(MAPE)和均方误差(MSE)。其计算公式分别为:


表3 两种方法预测结果的误差比较Tab.3 Comparison of the errors between forecasting results from two algorithms
3 结束语
非参数回归方法是一种不依赖于先验经验来归纳模型的方法,只要存在满足要求的历史数据库,任何路况下都能够进行预测且误差小。对于有异常路况出现的情况,该方法的优势更加明显。
本文在传统的非参数回归算法的基础上进行了两方面的改进,首先在基于聚类的历史数据中运用主成分分析方法得到状态向量,提高了算法的速度和准确性,然后采用增加反馈回路的方法使预测更加合理。
随着计算机技术的发展,当数据量日益增多时,如何更有效地提高算法的效率和准确性变得更为重要。只有不断地改进算法,才能适应交通的实时性和准确性,最终广泛应用于交通诱导等方面。
[1]杨兆升.城市交通流诱导系统理论与模型[M].北京:人民交通出版社,2000.
[2]姜桂艳.道路交通状态判别技术与应用[M].北京:人民交通出版社,2004.
[3]张晓利,贺国光.考虑交通吸纳点的非参数回归组合型短时交通流预测方法[J].系统工程,2006,24(12):21 -26.
[4]张晓利,贺国光,陆化普.基于K邻域非参数回归短时交通流预测方法[J].系统工程学报,2009,24(2):178 -183.
[5]张涛,陈先,谢美萍,等.基于K近邻非参数回归的短时交通流预测方法[J].系统工程理论与实践,2010,30(2):376 -385.
[6]王晓原,吴磊,张开旺,等.非参数小波算法的交通流预测方法[J].系统工程,2005,23(10):44 -48.
[7]刘燕,章洵.组合预测模型在短时交通流预测中的应用研究[J].物流管理,2010,23:15 -19.
[8]宫晓燕,汤淑明.基于非参数回归的短时交通流量预测与事件检测综合算法[J].中国公路学报,2003,16(1):82 -87.
[9]王璐.SPSS统计分析基础应用与实践[M].北京:化学工业出版社,2010.
[10]谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010.
