基于AR模型的磁流变减振系统动态性能研究

陈庆堂 黄宜坚

1.湄洲湾职业技术学院，莆田，351254 2.华侨大学，厦门，361021

0 引言

磁流变液(magnetorheological fluids，MRF)是一种智能软物质，具有强度高、黏度低、耗能小、温度稳定性好及对制造过程中产生的杂质不敏感等特点，在外加磁场作用下，能在毫秒级的时间内从牛顿流体变为高剪切屈服应力的黏塑性体，且这种转变过程是连续的、可逆的和可控的。近几年,磁流变技术显示出了强劲的发展势头，大量应用在阻尼元件、传动元件、精密加工、机械密封、液压系统、智能修复术等场合。采用磁流变技术制成的可调减振器，具有结构简单、响应快、动态范围广、耐久性好、不变质、阻尼大和噪声小等特点[1]。目前，磁流变减振系统的动力学建模主要是通过简化结构的方法建立二阶动力学模型，故其建模精度较低。本文研制了适用于混凝土砌块成形机的磁流变减振器，通过专用的振动测试工作台及振动信号的检测系统，改变了传统的建立系统简化二阶动力学模型的方法，建立了较为精确的减振系统的三阶动力学模型，并利用时间序列AR(autoregressive)模型自回归系数与连续系统分母多项式系数的对应关系推导出了三阶系统动态特性参数的计算公式，分析了系统的动态性能。其结果可为三阶减振系统动力学建模及其动态响应参数的计算提供理论参考[2]。

1 磁流变减振系统的结构组成

1.1 磁流变减振器结构设计

根据混凝土砌块机成形原理研制的磁流变减振器,可以根据不同砌块规格和配方,调节砌块机的阻尼使其与调频、调激励力相结合,实现砌块成形机的半主动控制,提高产品质量和劳动效率，节约能量。设计的磁流变减振器结构如图1所示。其结构由缸筒、活塞杆、线圈、橡胶块、磁流液、盖板等组成，设计中采用Q235A钢加工阻尼器的缸体和活塞等部件。缸体厚度对磁流变阻尼器力学性能无较大影响，如果缸体壁厚过小，会导致磁力线的磁阻过大。磁流变减振器的工作原理为：在工作过程中缸筒和活塞杆产生相对运动，磁流变液在活塞上下两腔产生压力差，在压差作用下磁流变液流动并在间隙处受到剪切作用，同时压力大的一腔还会对其产生挤压作用。本减振器设计时活塞与缸壁间隙h取1mm，活塞最大行程L取3mm。

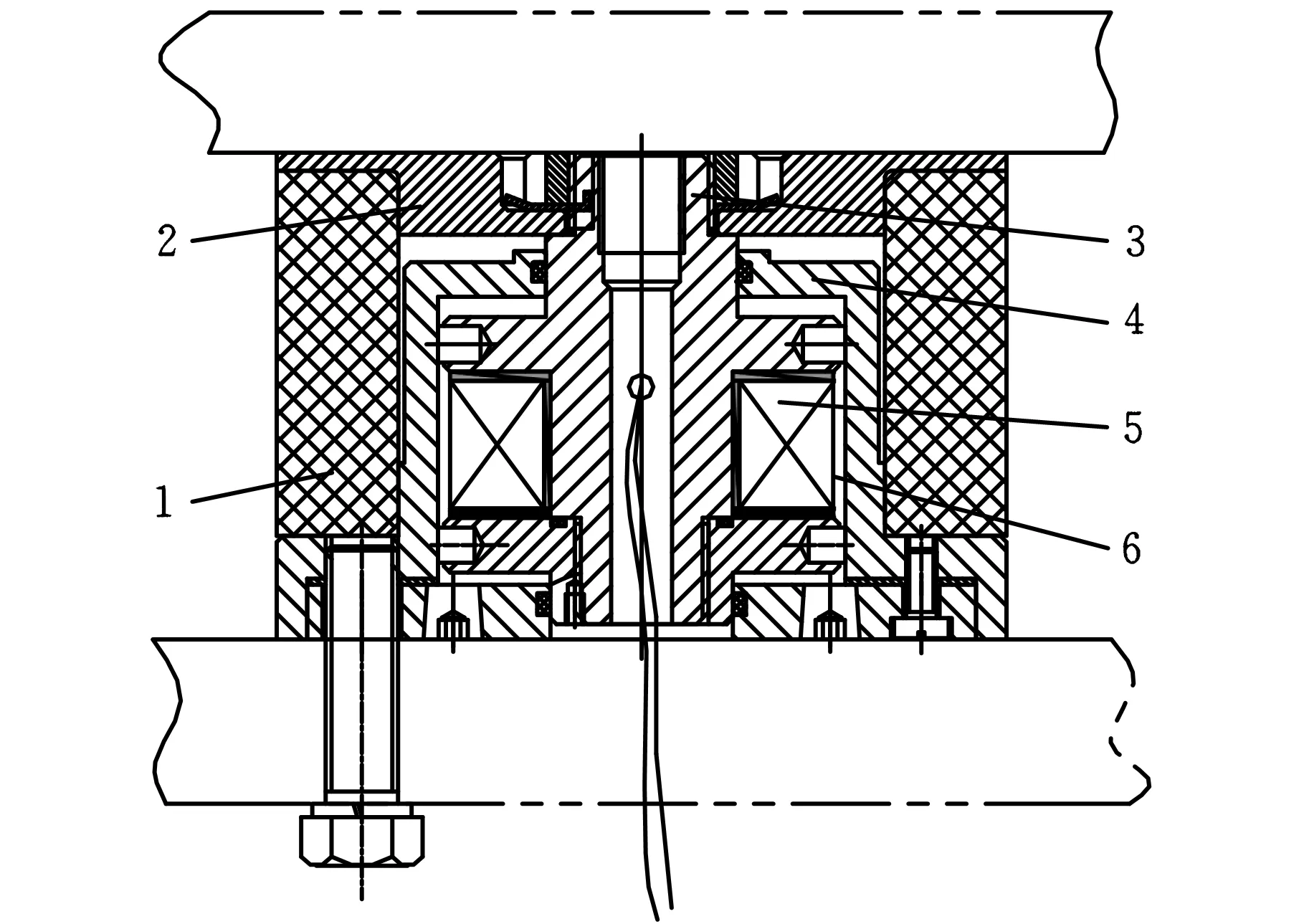
1.橡胶块 2.上盖板 3.活塞杆4.缸体 5.线圈 6.磁流变液图1 磁流变减振器的结构图

1.2 磁流变减振与测试系统组成

磁流变减振与测试系统是为了模拟砌块机的工作状态而设计与制作的，减振系统的结构由振动工作台、减振器组成，测试系统由变频电机、直流电源、变压器、信号采集卡、传感器、变频器、计算机软硬件组成，其原理如图2所示[3]。

图2 磁流变减振与测试系统结构简图

2 磁流变减振系统的动力学模型及动态特性参数的计算公式推导

2.1 减振系统的动力学模型[4]

减振系统通过变频器控制电机带动偏心轮产生减振激振力，在工作台与机座间安装磁流变减振器，减振器在外界电流的控制下产生不同磁流变效应而获得阻尼作用。激振力在减振系统的综合作用下获得位移输出值，根据图2中标注的各部分参数，设偏心轮的偏心距为Le，偏心轮的激振力f(t)=mω2Lesinωt,其中，m为偏心轮质量，ω为偏心轮角速度。振动台面质量为m1,阻尼系数为c1，弹性系数为k1；减振器活塞杆质量为m2，阻尼系数为c2，弹性系数k2。工作台与机座间弹簧的弹性系数为k3，由于活塞杆质量m2相对振动台面质量较小，可忽略不计，则建立系统微分方程如下：

(1)

(2)

式中，D、E、T1为简化后的常系数；ωn为无阻尼自然频率；ξ为阻尼比。

从式(2)可以看出,减振系统为三阶系统,其传递函数的特征根分别为[5]

(3)

式中，T为时间周期。

减振系统结构方块图如图3所示。

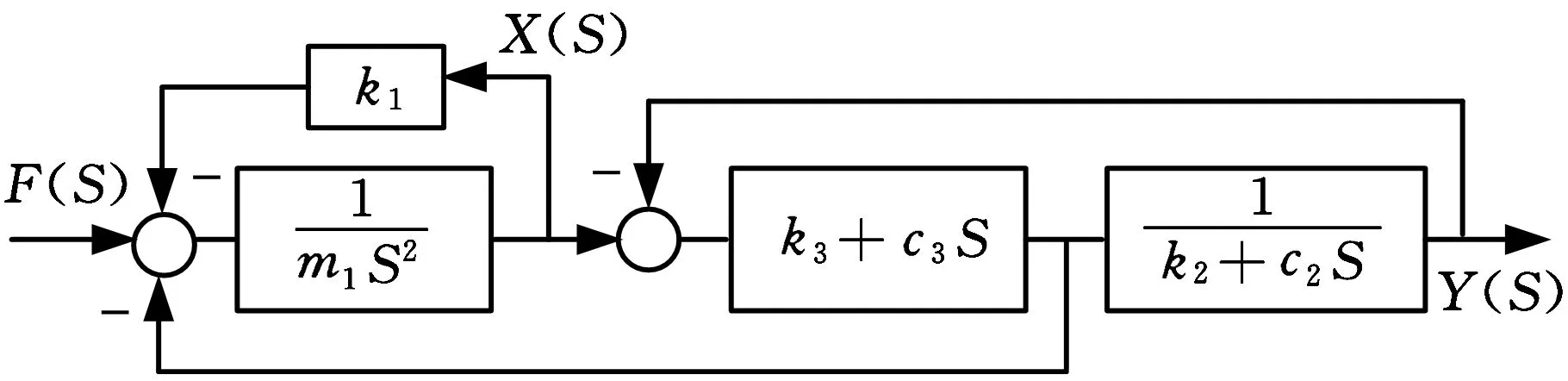
图3 减振系统结构方块图

2.2 振动信号时间序列的AR模型

对于采样获得的振动信号,可以建立三阶离散系统的时间序列AR模型：

xt-φ1xt-1-φ2xt-2-φ3xt-3=at

(4)

式中，at为白噪声；xt(t=1,2,3,…)为时间序列。

式(4)用后移算子B表示的方程为

(1-φ1B-φ2B2-φ3B3)xt=at

(5)

式(5)中的系数φ1、φ2、φ3采用自回归三阶AR(3)模型利用最小二乘(least square)法计算，计算公式为[6]

(6)

离散系统差分方程的分母多项式可表示为

(1-λ1B)(1-λ2B)(1-λ3B)=1-(λ1+λ2+λ3)B+
(λ1λ2+λ2λ3+λ3λ1)B2-λ1λ2λ3B3

(7)

2.3 三阶动态特性参数计算公式的推导

根据分母多项式系数的对应关系可列出以下方程组：

(8)

令

(9)

则式(8)可转化为

(10)

由式(10)可得

a3-φ1a2-φ2a-φ3=0

(11)

根据求解一元三次方程根的盛金公式，可得式(11)的一个实根和两个共轭虚根，因为式(9)中a为实数，则其实根为

(12)

(13)

式(10)中，b、c值分别为

(14)

(15)

(16)

故由式(16)可得出系统的阻尼比计算公式为

(17)

从而得出无阻尼自然频率的计算公式为

(18)

根据振动采样信号，利用式(17)、式(18)，获得系统的无阻尼自然频率ωn和阻尼比ξ，进而得到上升时间tr、峰值时间tp、调整时间ts和振荡次数N的计算公式[6]。

上升时间tr：

各向同性材料：本身具有各向同性属性的原料，多种物料均匀混合，各微小颗粒体虽然具有各向异性属性，但由于大量微小颗粒的随机分布，可以将其均匀混合物近似视为各向同性材料。配合饲料虽然由玉米等大量各向异性原料微粒混合而成，但由于大量微粒的随机分布和排列，可将模孔中的物料颗粒近似视为各项同性材料(武凯等，2013)。各向同性材料其实是横观各向同性材料的特殊情况。

(19)

峰值时间tp：

(20)

误差为2%的调整时间ts：

(21)

振荡次数N：

(22)

上升时间及峰值时间反映了系统响应的快速性，调整时间及振荡次数反映了系统的振荡性。

3 磁流变减振系统的实验检测与动态性能分析

3.1 实验检测

在进行减振系统的振动测试实验时，通过变频器控制振动台的马达转动频率，由此带动偏心轮以得到不同的激振力，激振力通过磁流变减振器在输出端利用传感器检测出位移信号，位移信号经采集卡后由PC机的LabVIEW可视化界面显示并在指定路径下保存。本实验使用PS-3030D直流电源控制电流变化，以研究不同电流下磁流变减振系统的性能，选用ST-1-03电涡流位移传感器检测位移信号，采用NI公司的PCI-601数据采集卡及前置处理器读取数据，选用哈乐滨泰达尔科技有限公司生产的磁流变液进行实验，磁流变液的密度为1.7g/cm3,零场黏度为0.27Pa·s，饱和剪切屈服强度为53.4kPa,质量因含量为81.79%[7-8]。

测试实验分别在频率为20Hz、25Hz、30Hz、35Hz、40Hz、45Hz和50Hz下进行，对应每个频率值检测控制电流分别为0、0.5A、1.0A、1.5A、2.0A和2.5A下的位移。数据采样频率为500Hz，每组采集10 000个数据，通过LabVIEW编写检测程序[9]。为了获得系统稳定的时间序列，在检测过程中每组数据在振动平稳后进行读取，为了防止磁流变液在长时间通电情况下会产生热量而影响其使用性能，在不同工作频率及不同控制电流下采用间断检测，待系统充分散热后进行另一状态的检测。

3.2 实验数据与处理

先对计算机读取稳定的位移信号范围进行零均值处理获得含有确定性信号的时间序列，计算在不同频率、不同控制电流下的方差和功率谱，不同控制电流与无控制电流时的时间序列方差比(即振幅比)列于表1，绘制的功率谱曲线如图4所示。采用中数法和五点平滑法滤去低频的确定性干扰信号成分获得系统分析的稳定的时间序列，建立AR(3)模型，利用推导出的三阶系统动态性能参数计算公式，计算得出减振系统的动态特性参数，绘制出不同控制电流及不同工作频率下动态响应参数变化曲线，结果如图5及图6所示。

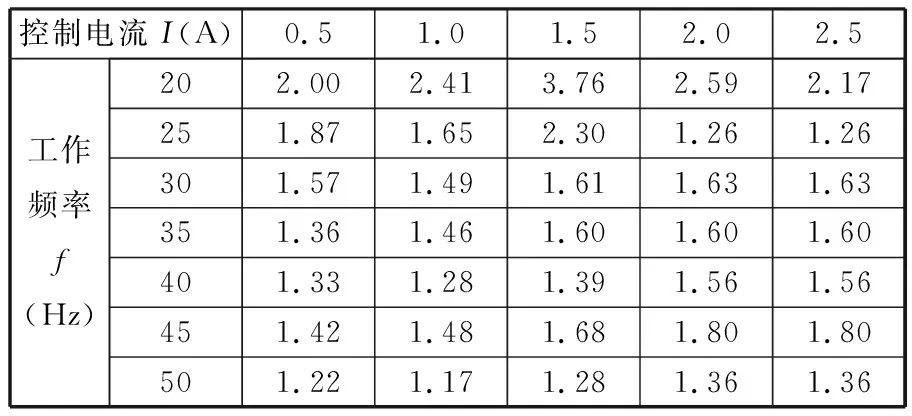
表1 减振系统在不同激振频率及不同控制电流下的方差比(振幅比)

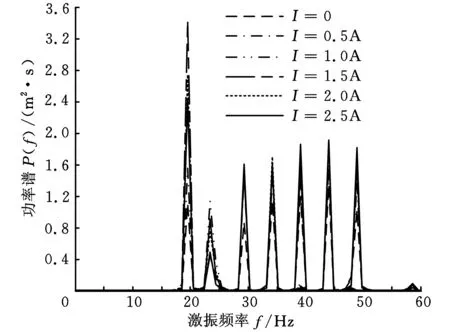
图4 不同控制电流下的振动信号功率谱曲线

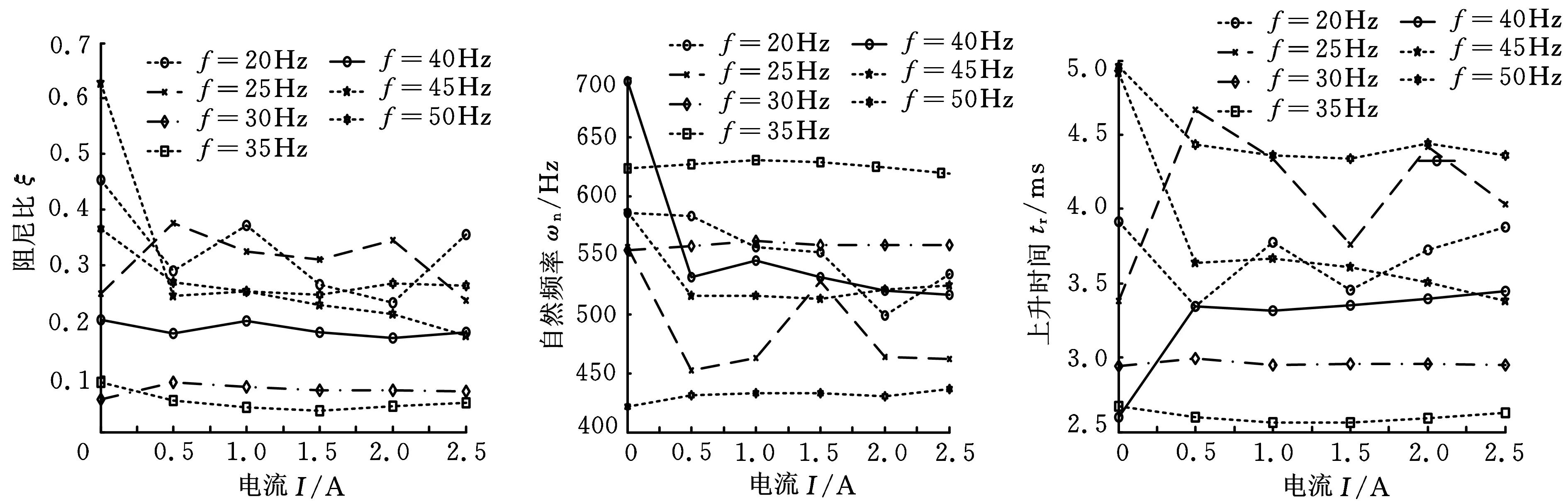
(a)阻尼比与电流值的关系 (b)自然频率与电流值的关系(c)上升时间与电流值的关系

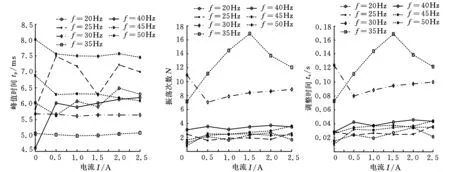
(d)峰值时间与电流值的关系 (e)振荡次数与电流值的关系(f)调整时间与电流值的关系图5 动态响应参数随控制电流变化曲线

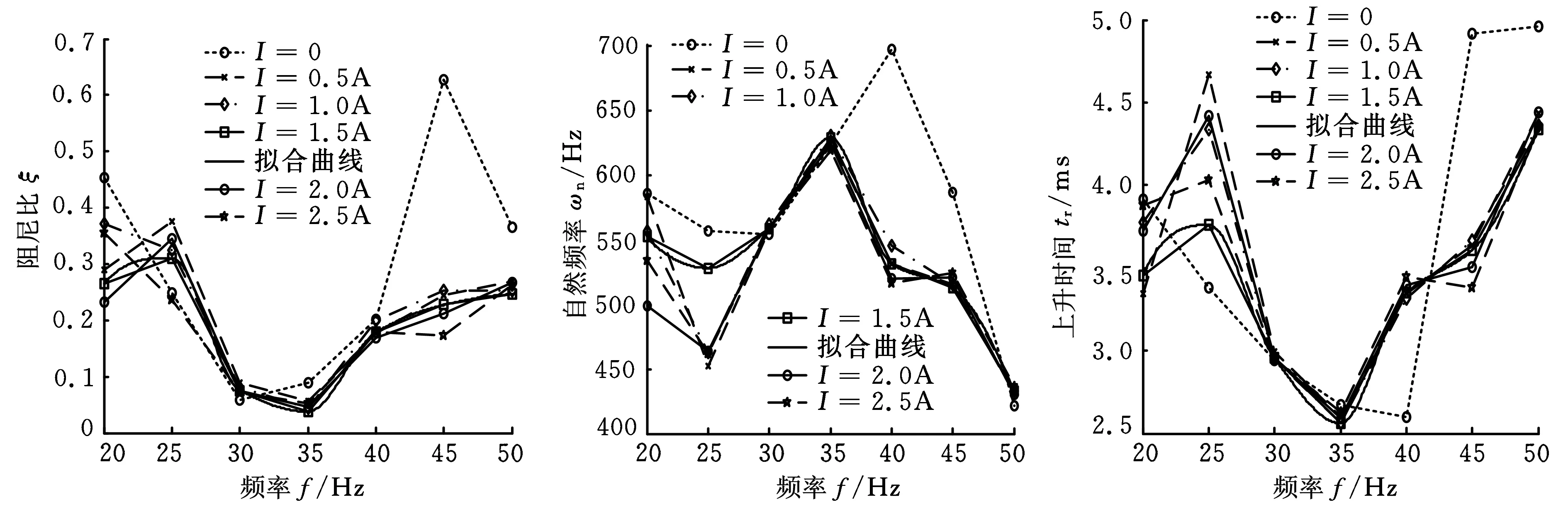
(a)阻尼比与工作频率的关系图 (b)自然频率与工作频率的关系图(c)上升时间与工作频率的关系图

(d)峰值时间与工作频率的关系图 (e)振荡次数与工作频率的关系图(f)调整时间与工作频率的关系图图6 动态响应参数随工作频率变化曲线

从功率谱曲线图4可以算出，曲线在对应工作频率处达到了峰值，系统的能量与工作频率存在明显的对应关系，表明系统的实验数据能够较为准确地反映其动态响应特征。从功率谱曲线还可以看出，不同控制电流下的峰值点高度不同，同一工作频率下无控制电流时的曲线峰值最小，随着工作频率的增大，最大峰值处对应的控制电流也随之增大。

3.3 实验结果分析

3.3.1减振效果

3.3.2动态性能分析

(1)阻尼比和无阻尼自然频率。从图5a可以看出：系统的阻尼比在施加控制电流后随着电流的增大总体上略呈下降趋势，在工作频率为20Hz及25Hz时，曲线波动较大，呈现出明显的非线性特征，在工作频率为30Hz、35Hz、40Hz条件下，电流的变化对阻尼比影响不大，在工作频率为45Hz、50Hz条件下，施加电流使阻尼比明显减小，但随着电流的增大阻尼比变化较小。从阻尼比与工作频率关系曲线(图6a)可明显看出，在相同电流下，系统的阻尼比随着工作频率的增大先减小后增大，在工作频率为35Hz时处于低谷。从图5b可以看出，在工作频率为30Hz、35Hz、50Hz时控制电流的变化对系统无阻尼自然频率影响不大，在工作频率为35Hz时自然频率值较高，在工作频率为40Hz、45Hz时控制电流的增大先使自然频率明显下降，后又趋于平稳，在工作频率为20Hz、25Hz时，无阻尼自然频率随控制电流的增大呈现下降趋势,但当电流大于1A后，曲线出现起伏波动。从图6b可以看出，同一控制电流下，无阻尼自然频率随工作频率的增大先增大后减小，在工作频率为35Hz时达到最大值，在25Hz时出现较小值，在50Hz时达到最小值。综合分析得出，工作频率在20～25Hz或35～50Hz、控制电流在0.5～2.0A条件下系统可获得较大的阻尼比,工作频率在20～40Hz、控制电流在0.5～1.5A条件下系统可获得较大的无阻尼自然频率。

(2)上升时间与峰值时间。从图5c、图5d可以看出，系统的上升时间与峰值时间这两个参数的变化趋势与控制电流变化的趋势一致，在工作频率为20Hz条件下，控制电流的增大使其值总体上呈先减小后增大的趋势；在工作频率为30Hz、35Hz时，控制电流的变化对系统的响应快速性影响不大，在工作频率为25Hz、40Hz时，随着控制电流的施加峰值时间及上升时间明显增大，随着电流的继续增大该两个参数总体上增大趋势减弱；在工作频率为45Hz、50Hz条件下，控制电流的增大使这两个参数先明显减小后基本不变，表明此工作频率下，施加控制电流时系统的响应明显加快但不随电流的增大而继续加快。在相同的控制电流下，上升时间与峰值时间随工作频率的变化曲线(图6c、图6d)呈“U”形，变化趋势与阻尼比变化趋势相近，也在工作频率为35Hz附近出现最低点，表明系统在这一频率附近响应较快。综合以上分析可得出,工作频率在20～40Hz、控制电流在0.5～2.5A时系统响应较快，其中工作频率在30Hz和35Hz时电流的变化对系统响应速度影响不大，工作频率在45～50Hz时系统响应较慢。

(3)调整时间及振荡次数。从系统的调整时间及振荡次数与控制电流的关系曲线图(图5e)可以看出，在同一工作频率下，随着控制电流的增大曲线呈上升趋势，系统的振荡加剧，在工作频率为35Hz且电流超过1.5A时曲线呈下降趋势;相同控制电流下,振荡次数随工作频率变化的曲线(图6e)呈倒“U”形，在工作频率为35Hz时曲线处于峰值，此工作频率下系统振荡加剧，与实验现象相吻合。综合以上分析可得出，工作频率在20～25Hz或40～50Hz、控制电流在0.5～1.5A下，系统的振荡较小。

综合响应快速性和振荡性，在0.5～1.5A低电流及20～25Hz低工作频率下系统具有较好的动态响应性能。

4 结论

(1)在建立磁流变减振系统动力学AR模型基础上，根据连续系统的传递函数与离散系统系数的对应关系推导出了三阶系统动态响应参数的计算公式。该公式能够推广用于三阶系统时间序列模型的动态性能计算与分析。

(2)设计的磁流变减振系统在施加控制电流时能获得明显的减振效果，尤其在低工作频率和1.0～2.0A的控制电流时减振效果较好。

(3)工作频率在20～25Hz或35～50Hz、控制电流在0.5～2.0A条件下，系统可获得较大的阻尼比,工作频率在20～40Hz、控制电流在0.5～1.5A条件下系统可获得较大的无阻尼自然频率。

(4)系统在工作频率为30Hz和35Hz时，控制电流的变化对系统动态性能参数影响不大。

(5)系统的动态性能参数随控制电流及工作频率呈现非线性变化，不同控制电流下各参数随工作频率的变化趋势一致。

(6)综合考虑系统的响应快速性与振荡性，该磁流变减振系统在0.5～1.5A低电流及20～25Hz低工作频率下具有较好的动态响应性能。

[1] 庄劲松，黄宜坚.砌块成型机振动信号的双谱自回归分析[J].机床与液压,2010(4):139-141.

[2] 黄宜坚,田天成,杨光胜.双主动圆盘式电流变传动器的数学模型[J].福州大学学报(自然科学版),2005(6):298-304.

[3] 杨叔子,吴雅.时间序列分析的工程应用[M].武汉:华中理工大学出版社,1994.

[4] 黄宜坚,刘晓梅,陈丙三,等.磁流变减振装置的自回归双谱分析[J].功能材料,2006(5):723-726.

[5] Zhan Yulong, Shi Zhubin, Shwe T. Fault Diagnosis of Marine Main Engine Cylinder Cover Based on Vibration Signal[C]//Proceedings of the Sixth International Conference on Machine Learning and Cybernetics.HongKong, 2007: 1126-1130.

[6] Shi Xiaochun,Hu Hongying.Diesel Engine Fault Diagnosis and Classification[C]//International Conference on Signal Processing Proceedings.Beijing,2006.

[7] Fisch A, Nikitczuk J, Weinberg B. Developmentof an Electro-rheological Actuator and Haptic Systems Forvehicular Instrument Control[C]//2003 ASME International Mechanical Engineering Congress and Exposition. Washington,2003: 15-21.

[8] Tsai Y Y ,Tseng C H,Chang C K. Development of a Combined Machining Method Using Electrorheological Fluids for EDM[J]. Journal of Materials Processing Technology, 2008, 201(1/3):565-569.

[9] Seok H Y, Seung K S, Jung H J, et al. Real-time Observation of Electrorheological Fluids Using Synchrotron X-ray Imaging[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2008,313/314: 557-561.