高阶椭圆锥齿轮齿形设计与加工
2012-11-30侯玉杰
林 超 龚 海 侯玉杰,2 聂 玲
1.重庆大学机械传动国家重点实验室,重庆,4000442.中国人民解放军96263部队,洛阳,471500
0 引言
非圆锥齿轮是用来传递两相交轴之间非匀速比运动的,它结合了非圆齿轮与圆锥齿轮的特点,具有体积小、运动平稳、传动效率高等优点[1]。非圆锥齿轮现在主要用在一些特殊的传动场合,如非圆锥齿轮限滑差速器、非圆锥齿轮变量泵等。随着对非圆锥齿轮研究的深入,这一新型的传动形式必然会应用到更多的场合,这就对非圆锥齿轮的设计、加工制造提出了进一步的要求。
齿形的设计是齿轮传动设计中一个重要的方面,齿形设计的优劣,关系到齿轮副是否可以按照预定的传动比进行传动,以及齿轮副啮合情况的好坏。非圆锥齿轮齿形设计尤为复杂,其中赵玉民等[2]、Xia等[3]根据不同的理论各自提出了非圆锥齿轮齿形设计的方法。本文基于传统的齿轮范成法原理来设计非圆锥齿轮的齿形。
非圆锥齿轮加工是限制其应用的主要瓶颈,目前在国内外,针对非圆锥齿轮的加工尚未提出很好的解决方法,相关研究还处于探索阶段[4-5]。CNC技术的日趋成熟和普及,特别是五轴联动数控机床的出现,很好地解决了复杂曲面的加工问题,且五轴联动数控机床加工精度高,这为非圆锥齿轮的加工制造提供了新的途径。
1 基本原理
椭圆锥齿轮副是一种典型的非圆锥齿轮传动形式,当将椭圆锥齿轮的极角缩小整数倍,就可演变出相应的高阶椭圆锥齿轮副,即对应演变成二阶椭圆锥齿轮副、三阶椭圆锥齿轮副、…、n阶椭圆锥齿轮副[6]。高阶椭圆锥齿轮的节锥面方程如下:
(1)
式中,n为主动轮的阶数;k为主动轮的偏心率;θ为高阶椭圆锥齿轮的周转角。
高阶椭圆锥齿轮实现的传动比为
(2)
1.1 高阶椭圆锥齿轮齿廓形成原理
由齿轮空间啮合原理可知,当高阶椭圆锥齿轮副传动时,两高阶椭圆锥齿轮的节锥面做相切纯滚动,若把其中一个高阶椭圆锥齿轮换成刀具(标准的圆锥齿轮),此时两者的传动表现为高阶椭圆锥齿轮的节锥面与圆锥齿轮刀具的节锥面做相切纯滚动。在啮合过程中,刀具的齿廓将会包络出与其具有相同渐开线形状的齿廓,这样即可获得高阶椭圆锥齿轮的齿形。
由上述原理可得到高阶椭圆锥齿轮在采用范成法进行加工的过程中,各运动参数之间的关系以及高阶椭圆锥齿轮齿形的生成过程。建立范成加工的坐标系,如图1所示,三维笛卡儿坐标系OXYZ的原点位于O点,Z轴竖直向上,Y轴水平向右;高阶椭圆锥齿轮的锥顶与原点O重合,高阶椭圆锥齿轮的回转中心轴与Z轴重合;刀具的自回转中心轴为OO1,在初始位置时,刀具的节曲线与高阶椭圆锥齿轮的节曲线相切于点M,OM与Z轴正方向夹角为ρ0;刀具节曲线相切于高阶椭圆锥齿轮的节曲线并做纯滚动,刀具绕Z轴转过角度θ1时,如图1所示,此时刀具节曲线与高阶椭圆锥齿轮的节曲相切于点M′,刀具的回转中心轴为OO′1,切线OM′与Z轴正方向夹角为ρ1。

1.高阶椭圆锥齿轮的节曲线 2.刀具节曲线3.刀具移动轨迹图1 范成加工的坐标系
图1中,δ为圆锥刀具的节锥角。

(3)
式中,R为高阶椭圆锥齿轮的球面半径。
刀具绕自身旋转轴转过的角度:
(4)
由图1知,ψ0=ρ0+δ,ψ1=ρ1+δ,刀具绕Y轴旋转的角度θy为
θy=ψ1-ψ0=ρ1-ρ0
(5)
综合式(4)、式(5),可以确定范成加工过程中,高阶椭圆锥齿轮与刀具范成运动时的运动变化关系如下:
(6)
根据以上齿廓成形原理,在Solidworks中利用其应用程序接口(API),开发高阶椭圆锥齿轮参数化仿真范成加工程序,运行结果如图2所示。

(a)二阶 (b)三阶(c)四阶图2 高阶椭圆锥齿轮包络齿廓
1.2 高阶椭圆锥齿轮齿面方程
根据上述高阶椭圆锥齿轮齿廓生成原理,由空间几何关系,利用解析法可以推导得到高阶椭圆锥齿轮的齿面方程。
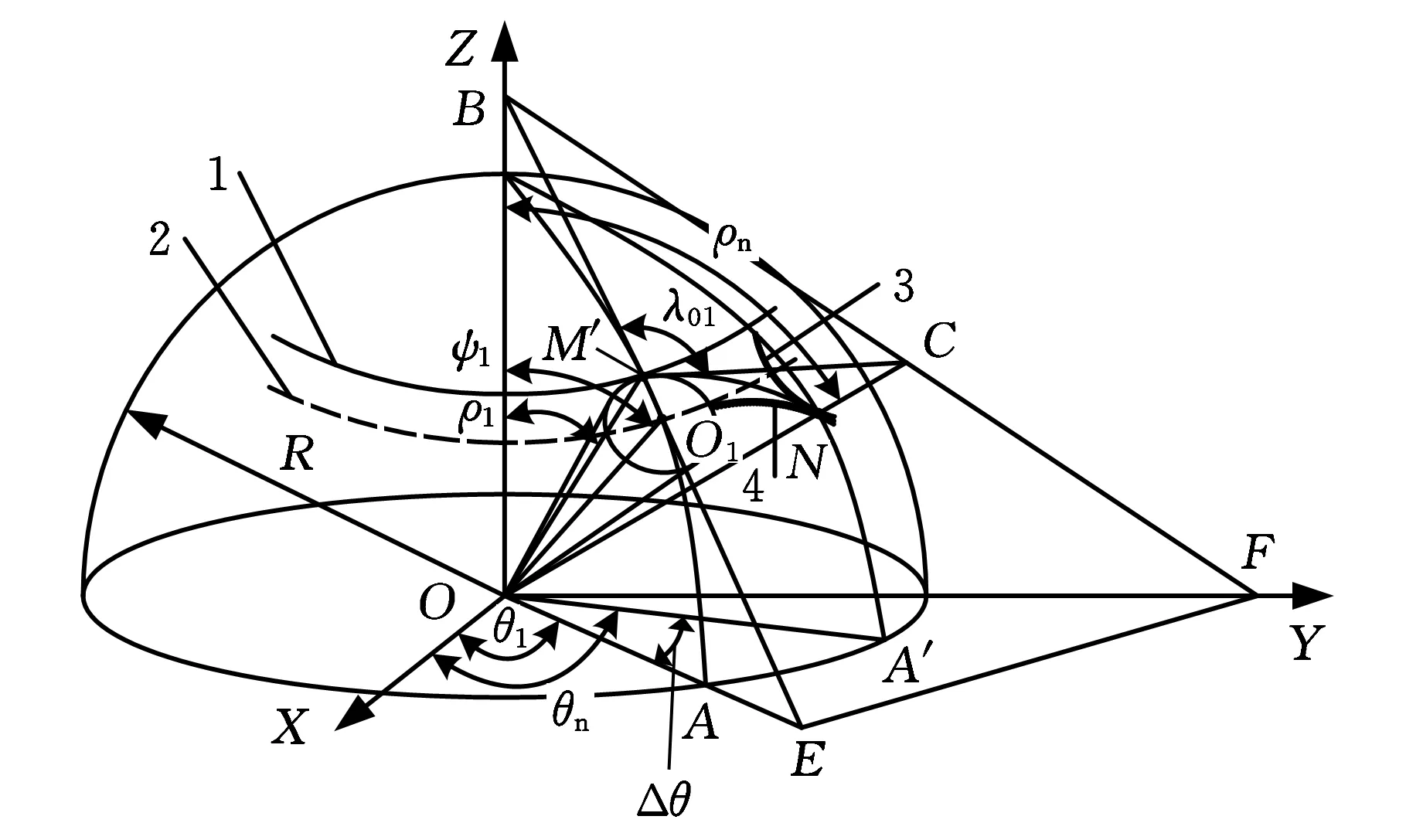
1.高阶椭圆锥齿轮的节曲线 2.刀具移动轨迹3.高阶椭圆锥齿轮齿廓 4.刀具齿廓图3 齿面的形成

在图3所示的位置,刀具节曲线在高阶椭圆锥齿轮节曲线滚过的弧长所对应的圆心角ψ为[7]
(7)
α=arcsin(sinψcosαn)
(8)
M′B与M′C的夹角λ01为
(9)
刀具齿廓与高阶椭圆锥齿轮的齿廓相切于点N,ON与Z轴的夹角ρn为
ρn=arccos(cosρ(θ1)cosα+sinρ(θ1)sinαcosλ01)
(10)
ON在XY平面的投影OA′与OO′1在XY平面的投影OA的夹角Δθ为
(11)
则综合式(10)、式(11),可得到高阶椭圆锥齿轮左上齿廓方程为
(12)
其中,θn为OA′与X轴正向的夹角。
根据齿廓点所在的位置,将高阶椭圆锥齿轮的齿廓分为:左边位于齿顶曲线与节曲线之间的左上齿廓;左边位于齿根曲线与节曲线之间的左下齿廓;右边位于齿顶曲线与节曲线之间的右上齿廓;右边位于齿根曲线与节曲线之间的右下齿廓。M′B与M′C的夹角因齿廓点所在的位置不同取值会有所不同,当齿廓点分别在左上齿廓、左下齿廓、右上齿廓、右下齿廓时,对应M′B与M′C的夹角分别为λ01、λ02、λ11、λ12,且λij(i=0,1;j=1,2)对应取值分别为
(13)
ζ2=arctan(tanαnsecψ)
同理可得高阶椭圆锥齿轮的左下齿廓、右上齿廓、右下齿廓方程,综合得高阶椭圆锥齿轮的齿廓方程
(14)
1.3 高阶椭圆锥齿轮的几何设计
1.3.1高阶椭圆锥齿轮的齿数Z1
在高阶椭圆锥齿轮传动过程中,轮齿的布局通常是将长轴端布置成齿槽,短轴端布置成轮齿。此时一对共轭齿轮的轮齿是对称分布的,轮齿啮合过程的受力状态可得到改善,且方便于设计及加工制造。此时高阶椭圆锥齿轮的齿数Z1须满足如下方程:
Z1=(2ε+1)n
(15)
式中,ε为正整数。
在设计过程中可根据实际的受力情况,确定正整数ε,从而确定高阶椭圆锥齿轮的齿数Z1。
1.4统计学方法采用SPSS21.0统计学软件对数据进行统计分析。计量资料以均数±标准差(±s)表示,采用t检验;计数资料以率(%)表示,采用X2检验。P<0.05表示差异具有统计学意义。
1.3.2高阶椭圆锥齿轮的球面半径R
由上述高阶椭圆锥齿轮的齿廓生成过程可知,高阶椭圆锥齿轮的球面半径R与圆锥刀具的球面半径R′相等,则可由圆锥刀具的基本参数确定高阶椭圆锥齿轮的球面半径R。
由齿轮啮合原理可知,圆锥刀具与高阶椭圆锥齿轮范成时,它们一个齿在节锥面上展开所对应的弧长必须相等,即可以得到方程:
(16)
式中,Z0为圆锥刀具的齿数。
由于式(16)中有Z0、δ两个未知数,则可以取定齿数Z0来求出节锥角δ,也可以取定节锥角δ来求出齿数Z0。同时,由于刀具其自身也要满足不发生根切的条件,其齿数Z0>17cosδ。
确定圆锥刀具的齿数和分锥角后,可由圆锥齿轮的尺寸计算公式得到圆锥刀具的球面半径R′:
(17)
从而可得高阶椭圆锥齿轮的球面半径R:
(18)
1.3.3高阶椭圆锥齿轮的齿宽B
由于高阶椭圆锥齿轮是一种新的锥齿轮传动形式,该种齿轮的齿宽B尚没有通用的计算公式,在此可借鉴圆锥齿轮的齿宽B的计算公式:
(19)
在设计和实际加工过程中,由式(19)求得齿宽B后,进行圆整,再根据实际受力情况进行调整。
1.4 高阶椭圆锥齿轮实体模型建立
在Solidworks中,利用其三维造型功能以及应用程序接口(API),根据上述所提出的高阶椭圆锥齿轮齿形的设计方法,开发出高阶椭圆锥齿轮实体建模的程序,建立高阶椭圆锥齿轮副的虚拟实体及其装配模型,如图4所示。

(a)二阶

(b)三阶

(c)四阶图4 高阶椭圆锥齿轮实体模型及装配体
2 五轴联动数控铣床加工过程
2.1 五轴联动数控铣床
高阶椭圆锥齿轮的加工,选用的是五轴联动数控铣床,铣床型号为SmartCNC500,其工作部分结构如图5所示,基本参数见表1。在铣床上共有5个数控轴实现复杂曲面的加工,可以把其运动轴分为刀具的运动轴和工件的运动轴。刀具运动轴包括沿X轴方向的平移运动Xt、沿Y轴方向的平移运动Yt及沿Z轴方向的平移运动Zt等三个平动轴;工件的运动轴由沿Z轴方向的旋转运动Zr和沿Y轴方向的旋转运动Yr两个旋转轴组成。
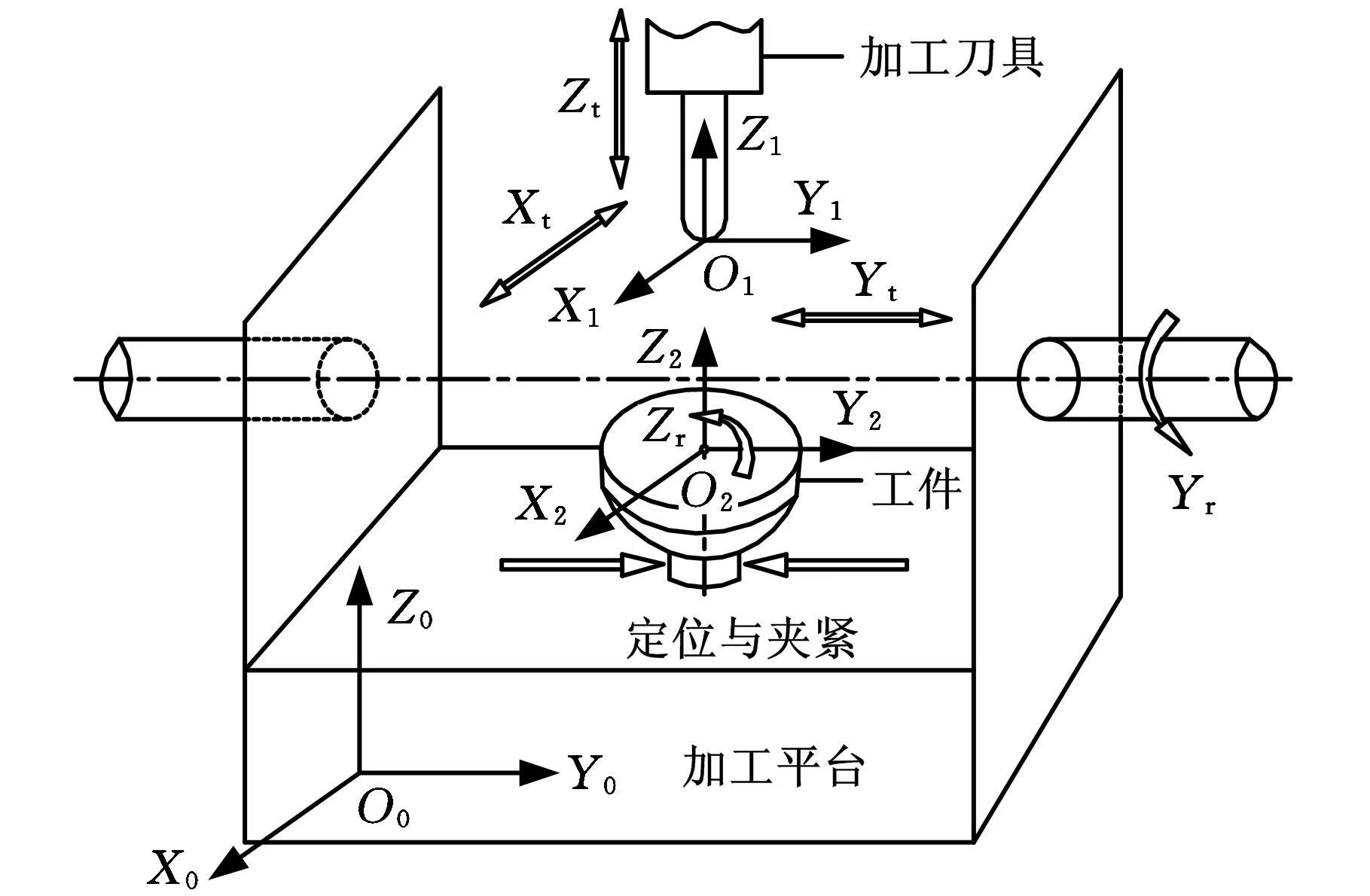
图5 五轴联动铣床结构与加工坐标系
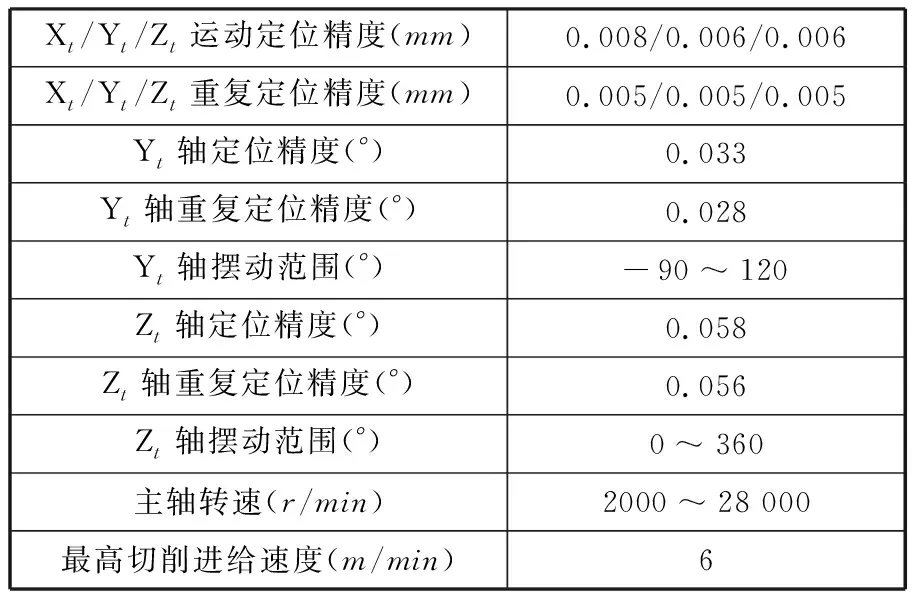
表1 五轴联动数控铣床基本参数表
2.2 五轴联动数控铣床的坐标系
如图5所示,建立铣床的固定全局坐标系O0X0Y0Z0、刀具坐标系O1X1Y1Z1(与刀具固连)、工件坐标系O2X2Y2Z2(与工件固连)。设初始位置时,三坐标系完全重合在铣床坐标系O0X0Y0Z0上。开始加工后,刀具坐标系O1X1Y1Z1在全局坐标系O0X0Y0Z0中沿X轴、Y轴及Z轴移动的距离分别为x、y、z,即刀具在铣床坐标系O0X0Y0Z0中平移的坐标为(x,y,z)。同时,由于工件的旋转,工件坐标系O2X2Y2Z2先绕其Z2轴旋转角度γ,再绕其Y2轴旋转角度η,由于工件坐标系O2X2Y2Z2只做旋转运动,全局坐标系原点O0X0Y0Z0和工件坐标系原点O2X2Y2Z2是完全重合的。
2.3 加工过程
由以上分析可得,刀具坐标系变换到铣床坐标系的变换矩阵为
(20)
即刀具在全局坐标系O0X0Y0Z0下的坐标为
(21)
工件坐标系变换到全局坐标系O0X0Y0Z0的变换矩阵为
(22)
即工件在全局坐标系O0X0Y0Z0下的坐标为
(23)
由式(21)~式(23)可得,刀具坐标系变换到工件坐标系的变换矩阵为
(24)
由以上的坐标变换关系,即可建立起数控加工时刀具与工件之间的位置变化关系。
毛坯加工完成后,依据以上提出的加工铣床及其坐标变换分析,编制加工所需的数控程序,即可进行高阶椭圆锥齿轮的加工。本次加工包括粗加工、半精加工和精加工三个程序。图6所示为各个齿轮加工过程图及获得的二阶、三阶、四阶椭圆锥齿轮样件,粗加工只需三轴联动即可完成,所以加工过程中只有刀具坐标系相对于机床坐标系的平移运动坐标变换。半精加工和精加工则必须采用五轴联动加工,此时除了刀具坐标系相对于铣床坐标系有平移坐标变换外 ,还包括工件坐标系相对于铣床坐标系的旋转坐标变换。

(a)二阶

(b)三阶

(c)四阶图6 加工过程与高阶椭圆锥齿轮
2.4 对滚检查
高阶椭圆锥齿轮运动检查,是将加工所得到的二阶、三阶、四阶椭圆锥齿轮,在对滚检查机上进行对滚检查试验,如图7所示。检查试验结果表明,采用本文方法加工出来的高阶椭圆锥齿轮副的啮合接触线轨迹接触良好,能够在全齿厚方向上全接触滚动。验证了范成法生成高阶椭圆锥齿轮齿廓模型的正确性,以及五轴数控精铣加工方法的可行性。

图7 对滚试验
2.5 啮合试验
高阶椭圆锥齿轮传动的试验台由一台变频直流电动机、变频控制器、转速扭矩传感器、位移传感器、联轴器、高阶椭圆锥齿轮传动箱、试验台架、计算机及数据采集处理软件等仪器及设备组成。二阶椭圆锥齿轮传动试验台如图8所示。

图8 二阶椭圆锥齿轮传动试验台
为测试转速,在输入/输出轴上分别安装了转速扭矩传感器。通过转速扭矩传感器测出输入/输出轴的转速,其比值即为所测传动比。依据搭建好的试验平台和制订的试验方案进行试验数据的测量和采集。将采集得到的数据经数据处理,即可获得二阶椭圆锥齿轮的试验传动比与理论传动比的对比结果,如图9所示。
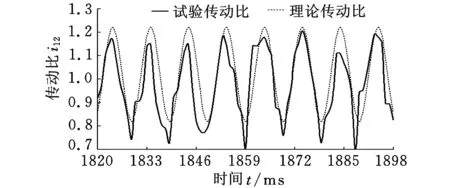
图9 传动比试验值与理论值对比
由图9可知,忽略加工制造误差、试验台的安装误差以及测量环境中一些不确定因素的影响,试验传动比曲线与理论传动比曲线相当吻合,表明了本文建立的高阶椭圆锥齿轮副的设计计算方法、齿廓生成方法及加工制造方法的正确性。
3 结论
本文基于齿轮空间啮合原理,分析了范成法生成高阶椭圆锥齿轮齿廓时,范成刀具的空间走刀位置,推导出了高阶椭圆锥齿轮的齿面方程;结合三维软件的二次开发,得到了高阶椭圆锥齿轮实体模型及虚拟装配体;建立了五轴联动数控铣床的坐标系,分别加工出了二阶、三阶、四阶椭圆锥齿轮,并通过对滚检查试验及啮合传动试验,验证了范成法生成高阶椭圆锥齿轮齿廓模型的正确性,以及五轴联动数控加工高阶椭圆锥齿轮制造方法的可行性。
[1] 谭伟明,梁燕飞,安军,等.渐开线非圆齿轮的齿廓曲线数学模型[J].机械工程学报,2002,38(5):75-79.
[2] 赵玉民,马延会,华林,等.非圆锥齿轮节曲线的平面展开算法研究[J].中国机械工程,2008,19(17):2046-2049.
[3] Xia Jiqiang, Liu Yuanyuan, Geng Chunming, et al. Noncircular Bevel Gear Transmission with Intersecting Axes[J]. Journal of Mechanical Design, Transactions of the ASME, 2008, 130(5): 1-6.
[4] 姜虹,王小椿.三周节变传动比限滑差速器设计与试验[J].农业机械学报,2007,38(4):31-34.
[5] 刘继胜, 罗姜.非圆齿轮的滚齿加工数控技术研究[J]. 机床与液压,2009,37(9): 62-65.
[6] 吴序堂,王海贵.非圆齿轮及非匀速比传动[M].北京:机械工业出版社,1997.
[7] 夏继强,耿春明,宋江滨,等.变传动比相交轴直齿锥齿轮副几何设计方法:中国,200410009582.6[P]. 2006-03-29.
