一种四自由度并联机构的性能指标分析
2012-11-30刘宏昭原大宁王庚祥
季 晔 刘宏昭 原大宁 王庚祥
西安理工大学,西安,710048
0 引言
机构的性能评价是机器人研究的重要内容之一,它对结构参数的选取和控制策略的拟定具有决定性作用。为了量化机构动力学性能,很多学者都曾做过相关研究。早在1982年,Salisbury等[1]采用Jacobian矩阵条件数研究了机构运动性能。1983年,Asada[2]采用广义惯性椭球研究了机器人动态性能特性。文献[3]将机构的Jacobian矩阵分离,分别研究了机构的移动性能和转动性能。文献[4]研究了一种8PSS冗余并联机构的动力学特性。近年来很多学者都曾对不同机构的运动特性进行过较为深入的研究[5-8]。
少自由度并联机构具有驱动元件少、成本低、结构紧凑和性价比高等优点,是近年来研究的热点[9]。为了更好地控制高速精密机器人,多角度研究机构的运动学和动力学性能具有十分重要的意义。本文通过改变4UPU机构中某个支链的运动副的布置方式,得到了一种变拓扑结构的具有四自由度的并联机构。根据机构结构特点和运动特性,建立了机构位置反解方程。利用求导法得到了机构一阶、二阶影响系数矩阵,分析了机构的运动学和动力学评价指标,得到了各指标与一阶、二阶影响系数矩阵之间的关系。考虑速度与角速度的量纲不同、力和力矩的量纲亦不同,将雅克比矩阵分离,单独研究机构的转动性能和移动性能。最后采用“分层”研究的方式,得到了机构各运动支链的加速度和惯性力性能评价结果。
1 机构结构及自由度分析
1.1 机构结构描述
图1所示的并联机构由4个UPU支链连接上下平台构成,其中3个支链的U副布置方式一致,通过改变另一支链U副的空间位置,得到了一种变拓扑结构的并联机构。与运动平台相连的U副用Ai(i=1,2,3,4)表示,与固定平台相连的U副用Bi(i=1,2,3,4)表示。为了便于描述,Ai和Bi还表示动平台和固定平台与支链的连接点。固定平台几何中心O为惯性坐标系原点,其中x轴平行于B1B2,y轴平行于B2B3;运动平台几何中心O′为动坐标系原点,初始位置时x′轴平行于x轴,y′轴平行于y轴,利用右手定则确定z轴。A1B1、A2B2和A3B3支链的U副转动轴线平行于x轴和z轴;另外一条支链的U副转动轴线平行于y轴和z轴。机构动平台边长为2a和2d,固定平台边长为2b和2c。
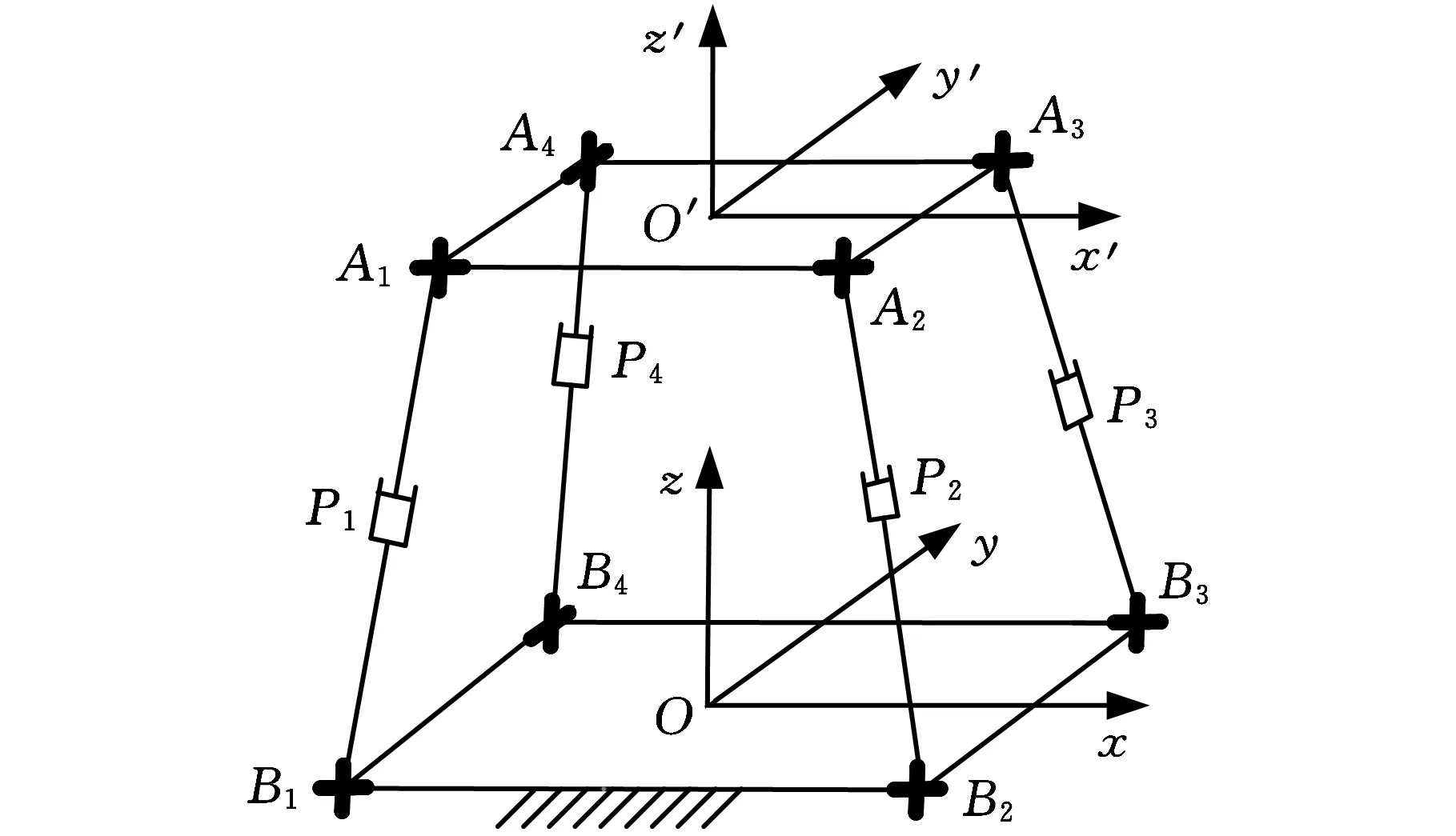
图1 变拓扑UPU并联机构结构简图
1.2 机构的结构演绎与自由度分析
原始机构为各支链结构相同的4-UPU机构。以B1为原点,各坐标轴方向与固定坐标系各轴方向相同建立螺旋坐标系,则A1B1支链运动螺旋为
反螺旋为
θx、θy、θz为支链与固定坐标系相应坐标轴的夹角。每个支链具有相同的反螺旋,因此机构自由度为5。由于机构只有4个驱动支链,此构型下机构不可控。
对机构中某条支链的U副进行调整。将A4B4支链的U副变为图1所示,其运动螺旋为
反螺旋为
此时机构动平台具有4个自由度,2个转动自由度被限制(绕x轴和y轴转动)。如果锁住AiBi支链的4个移动副,动平台自由度为0,机构输入合理。
2 机构位置关系方程的建立
经分析可知,机构具有空间3个移动和1个绕x轴转动的自由度,因此机构的动平台自由度用广义坐标可表示为X=(x,y,z,α)T。
各支链的矢量为
Ii=TxA′i+(x,y,z)T-Bi
(1)
i=1,2,3,4
其中,A′i为动平台各铰点在动坐标系下的向量;Bi为固定平台各铰点在惯性坐标系下的向量;(x,y,z)为动坐标系原点在固定坐标系下的矢量;Tz为动坐标系到惯性坐标系的旋转变换矩阵,即
式中,α为动平台绕z轴转动的欧拉角。
以各支链移动副作为输入,通过改变支链的长度来控制动平台的位姿,各支链长度为
(2)
式中,Ii(1)、Ii(2)、Ii(3)分别为各支链矢量的第一行、第二行、第三行元素。
3 运动影响系数的建立
并联机构的一阶、二阶影响系数求解方法主要有两种:封闭向量求导法和旋量法。由于已知机构的位置关系方程,因此采用前者进行求解。
3.1 一阶影响系数矩阵
机构的输入与输出速度关系满足:
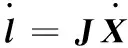
(3)
当J非奇异时,则
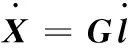
(4)
G=J-1
式中,J为各支链输入速度对动平台位姿速度的一阶影响系数矩阵;G为动平台位姿速度对各支链输入速度的一阶影响系数矩阵,即通常所说的Jacobian矩阵。
3.2 二阶影响系数矩阵
机构的输入和输出之间存在解析关系,J和G中各元素可表示为
Jij=f(x,y,z,γ)
Gij=f(l1,l2,l3,l4)
i,j=1,2,3,4
根据机构输入、输出速度关系方程式(式(3)、式(4)),分别对时间求导得
(5)
(6)
K和H可表示为
式(6)和式(5)为机构加速度正逆解方程。K和H分别为支链输入加速度对动平台位姿加速度的二阶影响系数矩阵和动平台位姿加速度对各支链输入加速度的二阶影响系数矩阵。Ki和Hi可作为第i条支链的二阶影响系数矩阵。
4 机构性能评价指标分析
机构的运动性能评价指标主要包括速度、加速度、承载力、驱动力和惯性力等。其中,速度、承载力、驱动力等由机构的一阶影响系数决定,而加速度和惯性力不仅与一阶影响系数有关,还与二阶影响系数有关,各性能指标分析如下。
4.1 速度性能指标
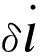
(7)
其中,‖G‖‖G-1‖是Jacobian矩阵的条件数,表示矩阵计算对误差的敏感性,是机构运动精度的度量,记为kG。kG越小,机构的速度偏差越小。
4.2 承载力、驱动力性能指标
机构的承载力是机构动平台承受的广义力,驱动力为各支链在动平台位于不同位姿时所承受的轴向力。定义支链输入的驱动力为f,动平台广义力为F。由于机构速度映射与力映射之间存在明显的对偶关系,则存在
F=GTf
因此机构的承载力和驱动力出现扰动,其性能评价与速度性能指标分析类似。
4.3 加速度性能指标
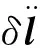
(8)
令
则有
存在
(9)
由于
即
存在
(10)
由式(9)和式(10)可知,加速度的扰动与‖G‖‖G-1‖和‖H‖‖H-‖有关,而‖H‖·‖H-‖为H的条件数,记为kH。kG和kH越小,机构的加速度偏差相对越小。
4.4 惯性力性能指标
惯性力F为质量与加速度的乘积,质量是不变量,不受扰动的影响。根据前述分析,性能指标需同时包含G和H,文献[10]采用g=‖G‖+‖H‖作为评价指标。为了得到各支链扰动对惯性力敏感程度,对机构的惯性力性能研究进行改进,采用如下评价方法:
gi=‖Gi‖+‖Hi‖
(11)
5 机构性能分析结果
图1所示机构的结构参数选取如下:a=0.23m,b=0.95m,c=0.36m,d=0.22m。根据实际任务空间,机构动平台中心点运动范围为x,y∈[-0.2m,0.2m],为了提高计算效率,分析性能指标时,均取z等于0.9m、1.0m和1.1m三个运动层为研究对象。机构的Jacobian矩阵G∈R4×4,其中前三行组成3×4矩阵,记为GT;最后一行为1×4矩阵,记为GR。GT和GR具有不同的量纲,分别作为速度和力、角速度和力矩的性能评定指标,因此kG的图谱由两部分组成,结果如图2所示。
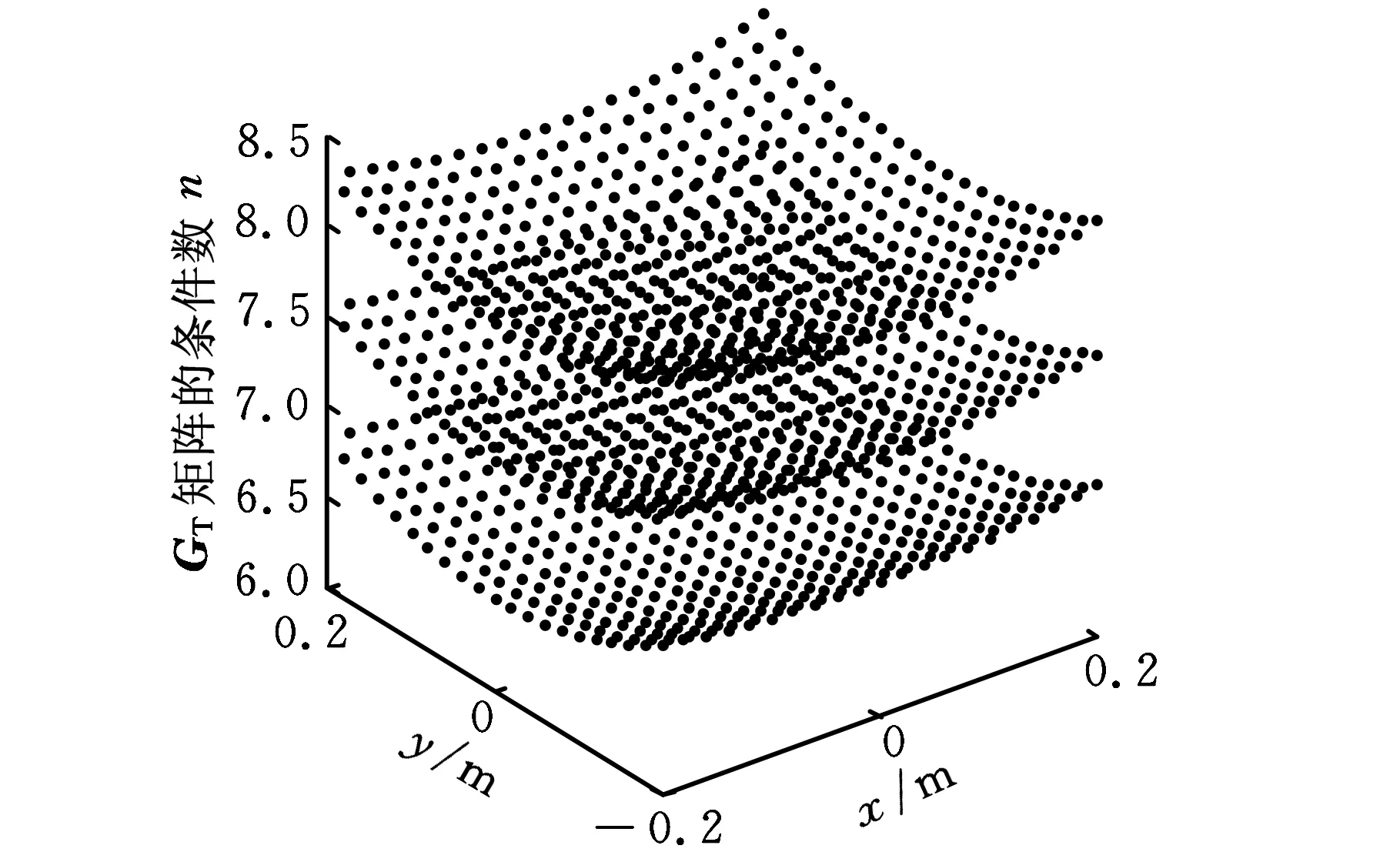
(a)对应GT的性能指标
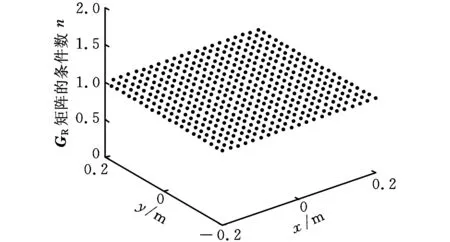
(b)对应GR的性能指标图2 kG性能指标图谱
GT的条件数性能图谱空间分布均匀,包含3层连续的曲面,从上到下各层分别对应于z等于1.1m、1.0m和0.9m。当动平台位于z=0.9~1.1m任务空间内时,GT条件数分布于z=0.9m和z=1.1m性能图谱构成的曲面之间;不管机构的动平台位于任务空间的任何位置,GR的条件数均为1。
为了更为细致地评定加速度性能指标,采用“分层”研究的方式,说明机构的加速度性能。根据上述分析可知,加速度性能由两部分决定,即输入扰动对M1和M2的影响。M1部分的指标分析如图2所示,M2部分的指标分析如图3所示。
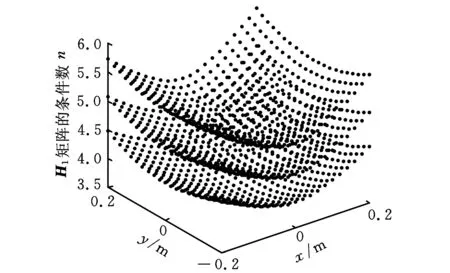
(a)A1B1支链的二阶影响系数性能指标

(b)A2B2支链的二阶影响系数性能指标
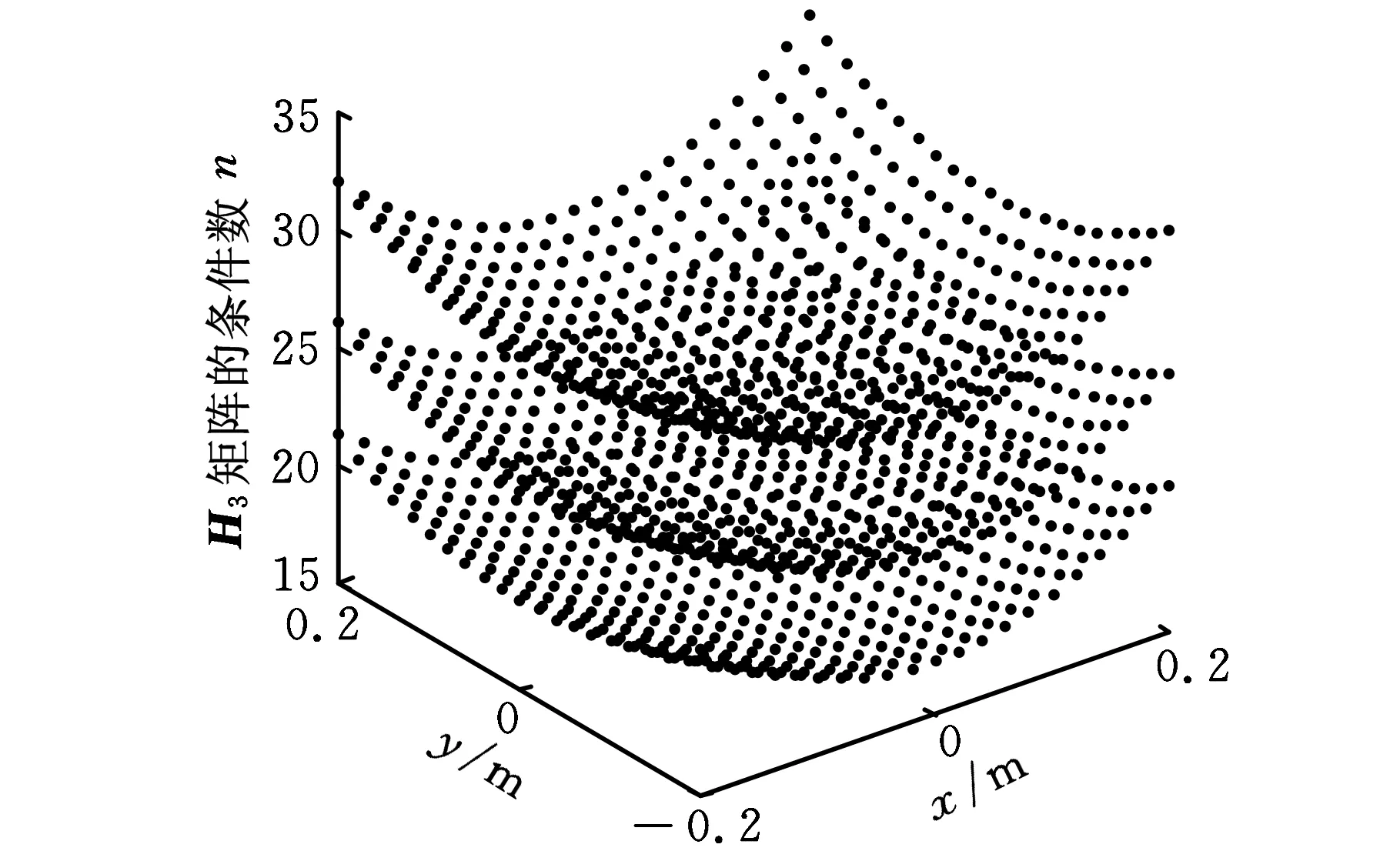
(c)A3B3支链的二阶影响系数性能指标
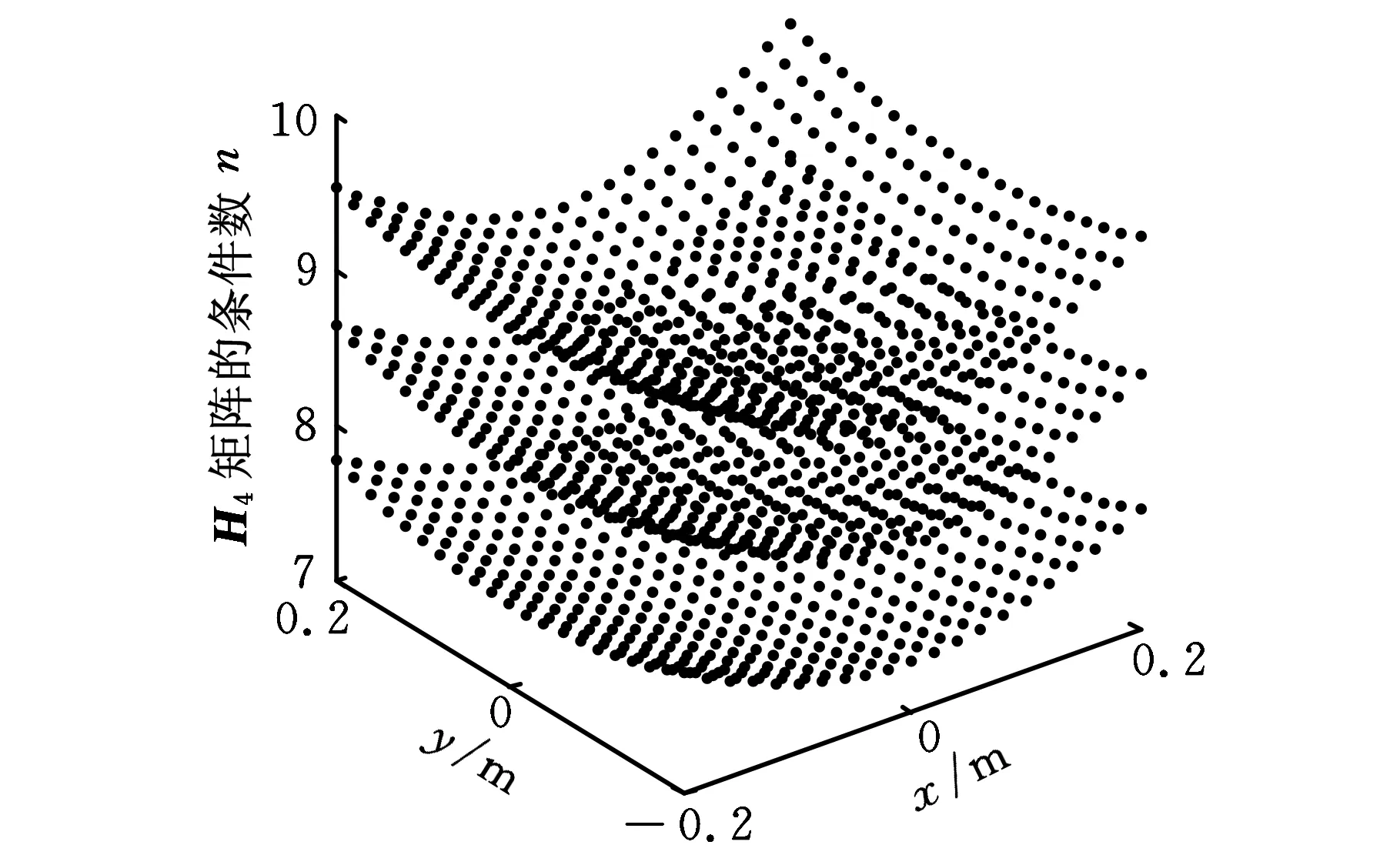
(d)A4B4支链的二阶影响系数性能指标图3 kHi性能指标图谱
kHi表示机构的第i条支链存在扰动时对M2的影响程度。第一、第四条支链对应Hessian矩阵的第一和第四层,从图3可以看出,这两条支链存在扰动时对动平台的影响相对较小,而第二、第三条支链存在扰动时,动平台受到的影响相对较大。
对机构惯性力的性能分析依然采用“分层”研究的方法,各支链的惯性力性能由g决定,计算结果如图4所示。
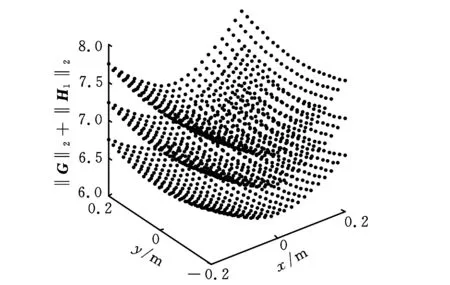
(a)A1B1支链的惯性力性能指标
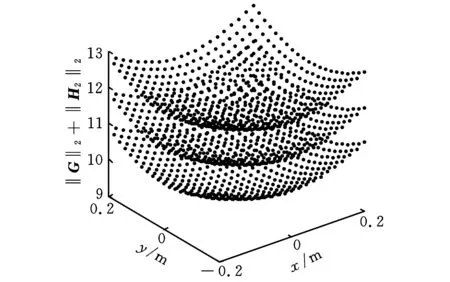
(b)A2B2支链的惯性力性能指标
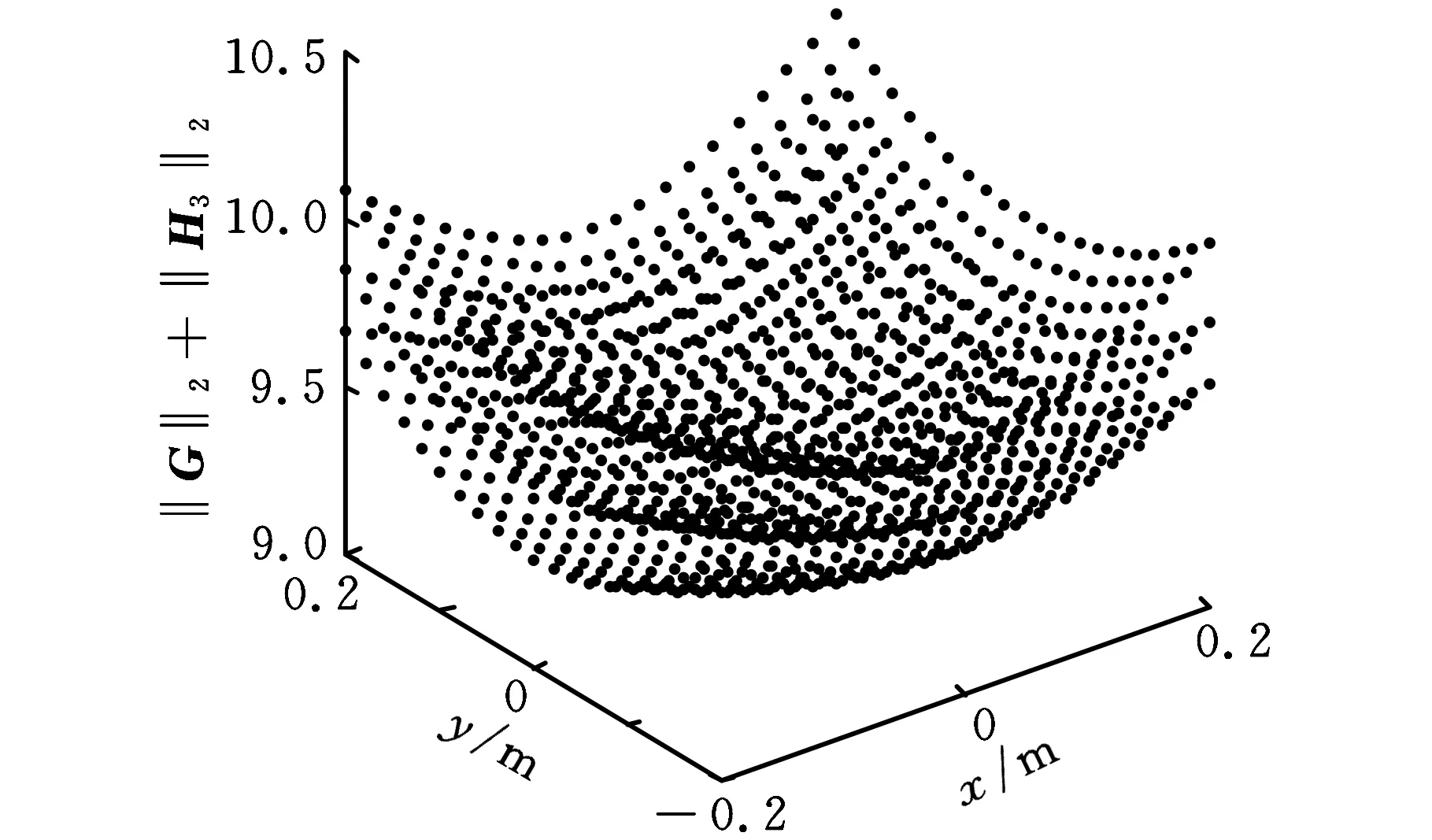
(c)A3B3支链的惯性力性能指标

(d)A4B4支链的惯性力性能指标图4 惯性力性能指标图谱
与加速度性能指标类似,第一、第四条支链的惯性力性能较好,其灵敏度和灵巧性好于第二、第三条支链。
在任务空间内,上述各性能指标计算结果范围如表1所示。
当运动平台和固定平台结构尺寸b、c和d恒定,a分别取0.2m和0.3m时,机构的GR的条件数不变,GT的条件数变化很小,Hi和gi的条件数随a的增大而增大;当运动平台和固定平台结构尺寸a、b和c恒定,d取0.2m和0.28m时,机构的GR的条件数不变,GT的条件数逐渐增大,而Hi和gi的条件数变化复杂,对应条件数均大于d=0.23m时的计算结果,尤其是H3的条件数发生“跳动”,最大值超过468;当运动平台和固定平台结构尺寸a、c和d恒定,b取0.9m和1m时,机构的GR的条件数不变,GT的条件数均大于b=0.95m时的值,同时Hi和gi的条件数也有所增大,其中H3的条件数也出现“跳动”,数值较大;当运动平台和固定平台结构尺寸a、b和d恒定,c取0.3m和0.4m时,机构的GR的条件数不变,GT的条件数均大于b=0.95m时的值,同时Hi和gi的条件数也有所增大,其中H3的条件数依然出现“跳动”,数值较大。
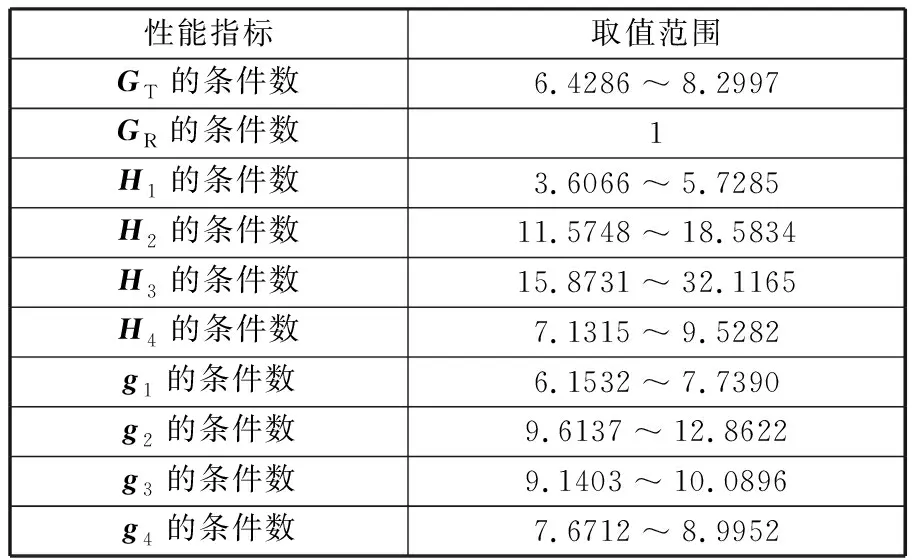
表1 性能指标范围
6 结语
通过改变机构一条五自由度并联机构支链的结构,得到了一种具有3个移动和1个转动自由度的并联机构。根据该变拓扑结构机构的位置关系方程,利用求导法得到了机构的正逆Jacobian矩阵和Hessian矩阵。由于机构的性能指标与两矩阵有直接关系,针对不同的性能指标,得到了各指标与两矩阵之间的映射关系。根据不同量纲,将Jacobian矩阵分离,分析了机构速度、承载力和驱动力性能,得到了任务空间内一阶性能图谱;利用“分层”研究的策略,得到了机构各支链与动平台之间的加速度性能和惯性力性能,得到了二阶性能图谱。
计算结果表明,按照文中的尺寸参数选取,机构各性能指标在任务空间内变化较小且分布均匀,具有良好的对称性,运动学和动力学性能较好。如果改变上平台或下平台的某个结构参数可能会使机构某些性能严重下降,如H3的条件数过大,造成输入和输出之间加速度关系失真。上述分析为机构的结构参数确定提供了依据。
[1] Salisbury J K, Craig J J. Articulated Hands Force Control and Kinematics Issues[J]. International Journal of Robot Research, 1982, 1(1): 4-17.
[2] Asada H. A Geometrical Representation of Manipulators Dynamics and Its Application to Arm Design[J]. Transaction of ASME Journal of Dynamic Systems, Measurement and Control, 1983, 105(3): 131-142.
[3] Philippe C, Samuel B, Clement G. Kinematic-sensitivity Indices for Dimensionally Nonhomogeneous Jacobian Matrices[J]. IEEE Transaction on Robotics, 2010, 26(1): 166-173.
[4] Zhao Yongjie, Gao Feng. Dynamic Performance Comparison of the 8PSS Redundant Parallel Manipulator and Its Non-redundant Counterpart—the 6PSS Parallel Manipulator[J]. Mechanism and Machine Theory, 2009,44:991-1008.
[5] Liu Xinjun, Wang Jinsong, Pritschow G. Performance Atlases and Optimum Design of Planar 5R Symmetrical Parallel Mechanisms[J]. Mechanism and Machine Theory, 2006,41(2):119-144.
[6] Imed M, Mohammed O. The Power Manipulability-a New Homogeneous Performance Index of Robot Manipulators[J]. Robotics and Computer-integrated Manufacturing, 2011, 27(2):434-449.
[7] Georg N. New Performance Indices for 6-dof UPS and 3-dof RPR Parallel Manipulator[J]. Mechanism and Machine Theory, 2009, 44(1):208-221.
[8] Wu Jun, Wang Jinsong, Wang Liping, et al. Performance Comparison of Three Planar 3-DOF Parallel Manipulators with 4-RRR, 3-RRR and 2-RRR Structures[J]. Mechatronics, 2010, 20(4): 510-517.
[9] Xu Qingsong, Li Yangmin. An Investigation on Mobility and Stiffness of a 3-DOF Translational Parallel Manipulator Via Screw Theory[J]. Robotics and Computer-integrated Manufacturing,2008,24(3): 402-414.
[10] 刘爽,郭希娟,刘彬.4-RR(RR)R并联机构的动力学性能指标分析[J]. 机械工程学报,2008,44(7):63-68.
