京新高速上地斜拉桥抗震设计分析

辛 兵 王克海 徐升桥

(1.中铁工程设计咨询集团有限公司，北京 100055;2.交通运输部公路科学研究所，北京 100088)

斜拉桥由于跨越能力大，造型优美流畅，布局较容易与周围环境相协调统一，近年来在城市桥梁建设中被广泛采用。斜拉桥既能满足结构要求，又具有景观效果，往往成为城市具有标志性的建筑。大跨径斜拉桥作为城市交通路线上的枢纽工程和生命线工程，若遭受地震灾害破坏，无论重建还是改线绕行都较为困难，并影响救灾工作的顺利进行，造成重大的经济损失。因此，对大跨径斜拉桥进行合理、有效的抗震设计，以确保其在大震中的安全性，具有十分重要的社会和经济意义。

1 工程概况

京包高速公路工程上地铁路分离式立交公路大桥位于京包高速公路(北京市五环路—六环路)上，本桥采用(46+46+230+98+90)m五跨连续独塔单索面预应力混凝土半漂浮体系斜拉桥，全桥长510m。主塔为倒Y形塔，采用塔、墩固结体系，主梁支承于塔墩上，塔高99m，索塔高度与中跨比为0.38，主梁主跨的跨高比为1/68(如图1所示)。

本桥需跨越城铁13号线、既有京包铁路以及京张城际铁路，抗震安全问题显得尤为重要。根据《中国地震参数区划图》(GB 18306—2001)，本区地震动峰值加速度为0.20g，地震基本烈度为Ⅷ度，按Ⅸ度设防。按照现行《公路桥梁抗震设计细则》(JTG/TB02—01—2008)，其抗震设防类别为A类，抗震设防目标既要保证桥梁的抗震安全性，又不致使造价增加太多，需要在经济性与安全性之间进行合理平衡，这是桥梁抗震设防的合理原则。

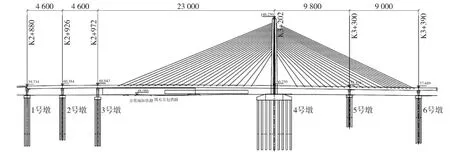
图1 全桥结构形式(单位:cm)

根据本桥桥梁结构各部分的重要性，以及地震破坏后桥梁结构的性能要求、修复(抢修)的难易程度，主桥采用50年超越概率10%(E1)、2%(E2)地震作用输入作为设防标准，见表1。

表1 桥梁抗震校核准则

2 全桥空间有限元模型

采用MIDAS有限元程序，建立三维有限元动力计算模型进行抗震性能分析，计算模型均以顺桥向为X轴，横桥向为Y轴，竖向为Z轴;主梁采用单梁模拟，拉索采用桁架单元模拟，主塔采用三维梁单元模拟，承台按梁单元模拟;进入土体的桩基础部分考虑桩—土—结构相互作用，采用六自由度土弹簧进行模拟，土弹簧刚度采用“m”法确定(如图2所示)。

本桥在所有桥墩墩顶及桥塔处分别设置了纵向或多向活动盆式橡胶支座，根据《公路桥梁抗震设计细则》(JTG/T B02—01—2008)，有限元建模时应考虑活动盆式支座的影响，活动盆式支座可用双线性理想弹塑性弹簧单元模拟，其初始刚度k按下式计算

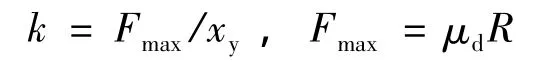
式中，μd为滑动摩擦系数，一般取0.02;R为支座承担的上部结构重力;xy为活动盆式支座屈服位移，一般取0.002～0.005m。

图2 斜拉桥动力计算有限元模型示意

3 自由振动特性分析

分析和认识桥梁的动力特性是进行桥梁抗震性能分析的基础。在小震作用下考虑盆式支座水平摩擦力提供的初始刚度，对本桥(模型一)进行模态分析得到全桥前100阶周期与振型，取前10阶模态的频率与振型，如表2所示，前4阶振型图如图3～图6所示。在大震作用下主梁与盆式支座在活动方向发生滑动，支座不能提供水平刚度约束，按不考虑支座的影响(模型二)对本桥进行模态分析得到全桥前100阶周期与振型，取前10阶模态的频率与振型，如表2所示，前4阶振型图如图3～图6所示。

从以上斜拉桥自振特性分析可知，对于模型一，考虑盆式支座的影响，在振动时对主梁提供水平约束，因此表现出斜拉桥的第1阶模态为主梁的竖向弯曲振型，第2阶振型才出现全桥纵漂振型，表明斜拉桥全桥竖向刚度小于纵向刚度;第3阶仍为主梁的竖向振动振型，第4阶为主梁反对称侧弯振型，第9阶为主塔侧弯振型，说明斜拉桥桥塔横桥向刚度大，对抵抗地震动作用非常有利。对于模型二，是基于大震作用下，盆式支座在活动方向主梁与支座发生相对滑动，支座不能提供水平约束，纵向刚度小于全桥的竖向和横向刚度，其第1阶模态表现为全桥纵漂振型，第2阶模态为主梁竖弯振型，第3阶模态为主梁侧弯振型，表明主梁横向刚度大于竖向刚度;第7阶模态出现桥塔的侧弯振型，表明桥塔横向刚度大。

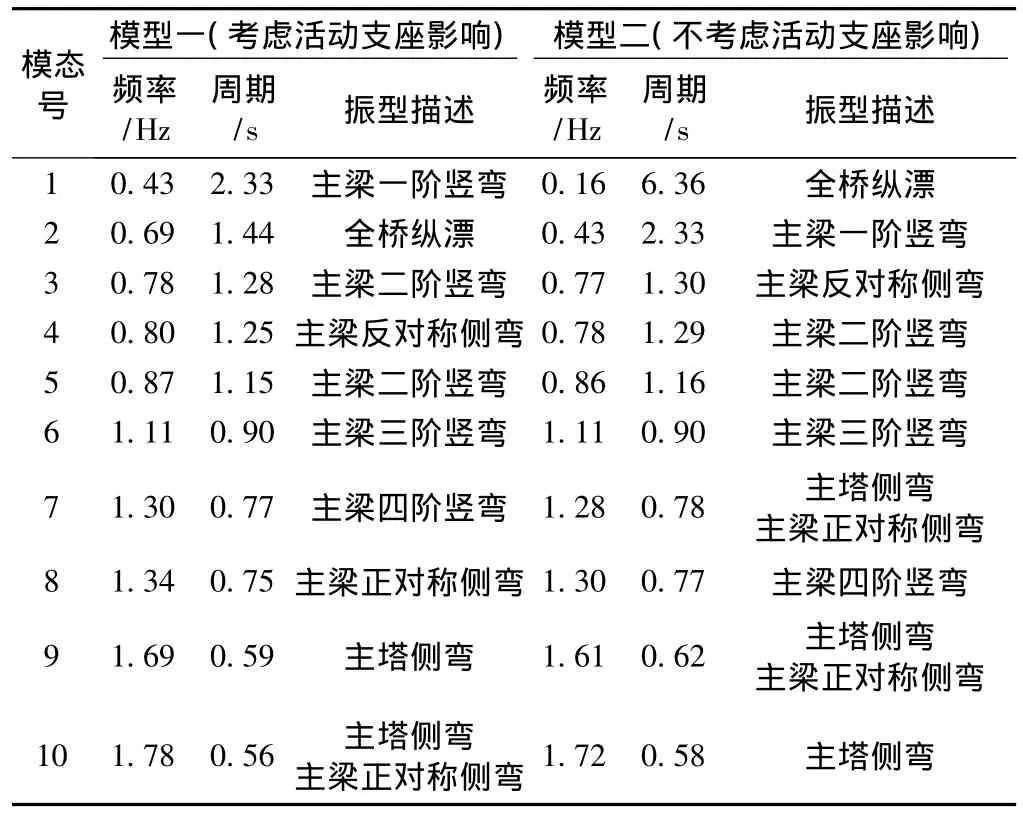
表2 前10阶频率及振型

图3 主梁一阶竖弯(模型一第1阶模态、模型二第2阶模态)

图4 全桥纵漂(模型一第2阶模态、模型二第1阶模态)

图5 主梁二阶竖弯(模型一第3阶模态、模型二第4阶模态)

图6 主梁反对称侧弯(模型一第4阶模态、模型二第3阶模态)

4 反应谱分析

4.1 反应谱输入

反应谱理论也称动力法，是目前世界各国应用最为广泛的抗震分析方法，其优点是考虑了地震时地面的运动特性与结构物自身的动力特性，计算量少，且加速度反应谱值是加速度反应的最大值，用它来控制设计一般是安全的。

本桥位处地震基本烈度为Ⅷ度，按Ⅸ度设防，地震动峰值加速度为0.20g，E1地震作用下水平设计加速度反应谱最大值Smax=0.45g，E2地震作用下水平设计加速度反应谱最大值Smax=0.765g，对于竖向地震系数取水平向的0.67倍(如图7所示)。

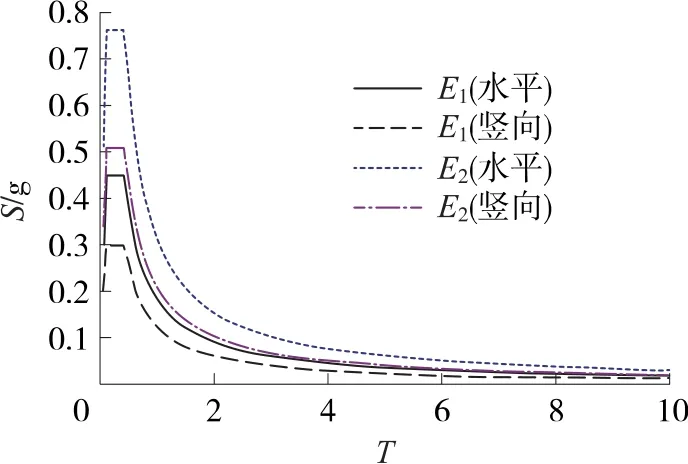
图7 反应谱

采用多振型反应谱法计算，所考虑的振型阶数应在计算方向获得90%以上的有效质量。本文计算了前100阶自振周期和振型参与系数，其累积振型参与质量见表3，其中顺桥向X、横桥向Y，竖向Z。

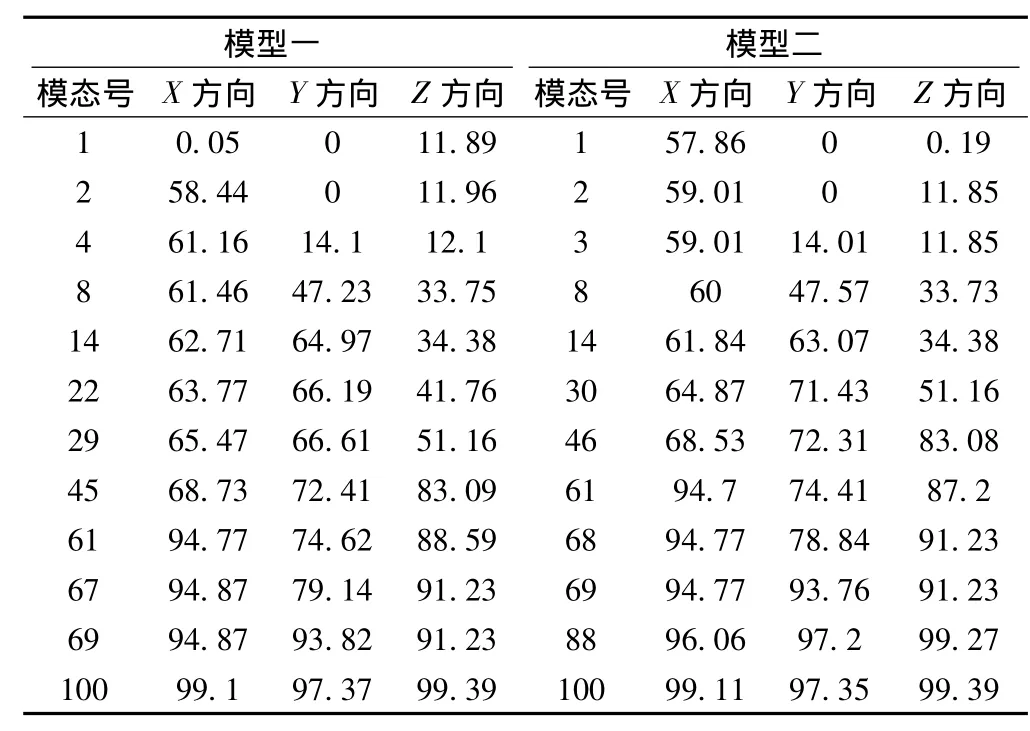
表3 累积振型参与质量_

从表3中数据可知，各振动方向在第100阶模态的累积振型参与质量到达95%以上，满足反应谱分析模态数量的要求。结构的振型组合采用CQC法，同时考虑顺桥向X、横桥向Y与竖向Z的地震作用，方向组合采用SRSS法。

4.2 计算结果分析

(1)模型一(考虑活动支座的影响)

本斜拉桥在地震作用下验算的关键截面主要是两侧桥塔根部和边跨各桥墩墩底截面，以及验算盆式支座的位移和水平承载力(如表4、表5、表6所示)。

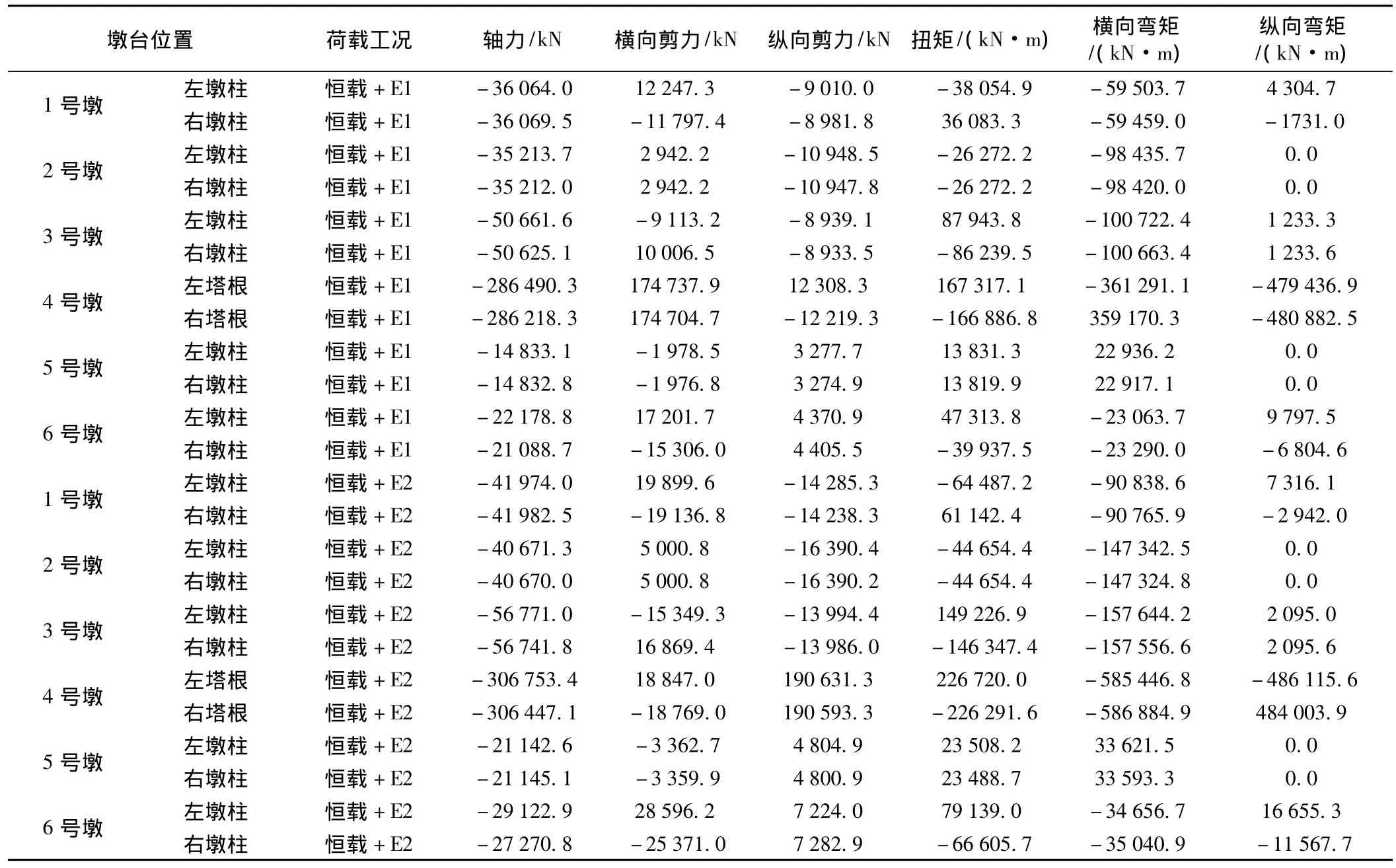
表4 关键截面内力(模型一)

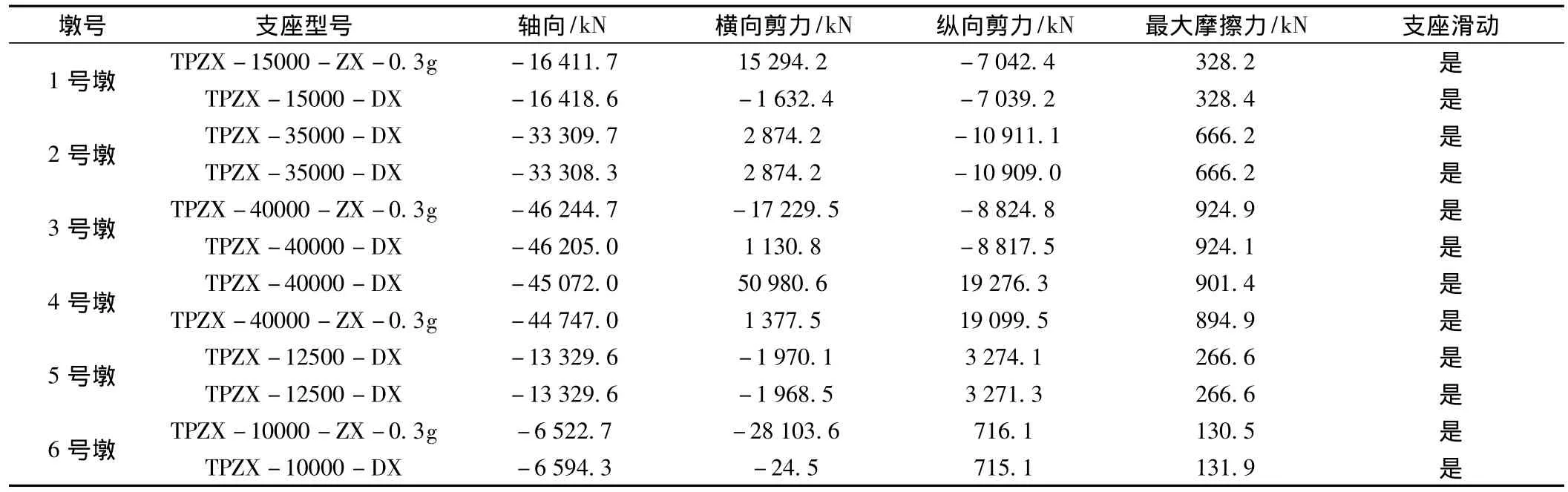
表5 恒载+E1地震作用下支座反力(模型一)

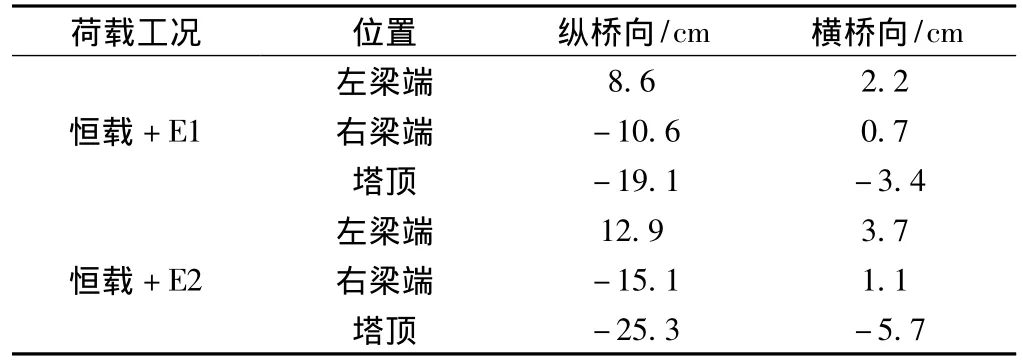
表6 地震作用下梁端及塔顶位移

从表5可知，在E1地震作用下，盆式支座的活动方向所受的水平力大于支座能提供的最大静摩擦力，主梁体与支座在活动方向发生相对滑动，因此在E1地震作用下不应考虑盆式支座的水平刚度影响。

(2)模型二(不考虑活动支座的影响)

不考虑盆式支座活动方向的水平刚度影响，重新计算全桥结构关键截面内力，计算结果如表7～表9所示。

(3)计算结果分析

通过对比模型一和模型二的模态分析和反应谱计算结果，可以看出:

①模型一的刚度比模型二大，因此其基频比模型大，对应于相同的反应谱函数，模型一所受到的地震加速度大于模型二。

②考虑盆式支座活动方向主梁与支座之间静摩擦影响所产生的水平刚度，将增大全桥结构纵向刚度，导致大跨柔性的斜拉桥体系第一阶模态表现为主梁竖弯振型，其次是由纵向刚度引起的纵漂振型。模型二的结构纵向刚度完全由主塔提供，其刚度一般小于全桥竖向和横向刚度，表现出第一阶模态为纵漂振型，其次是主梁竖向弯曲振型。

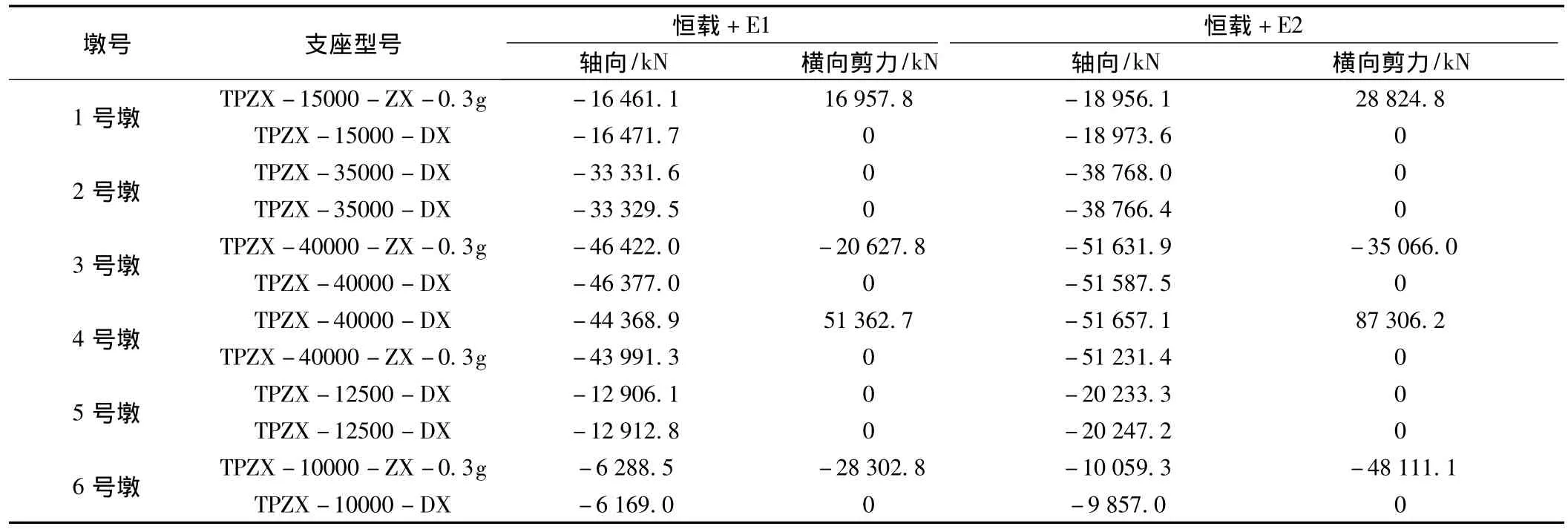
表8 地震作用下支座反力(模型二)

表9 地震作用下梁端及塔顶位移(模型二)

③模型一在地震作用下，由于考虑了盆式支座的影响，在支座活动方向将有水平力通过支座传递到下部结构，引起墩底相应方向的水平力和弯矩;而模型二不考虑支座活动方向刚度的约束，其墩底剪力和弯矩比模型一小。对于桥塔结构两侧的根部截面，由于纵向活动支座不分担由地震荷载引起的水平力，因此模型二在该截面处的纵桥向剪力和弯矩均大于模型一。

④地震作用下支座的水平反力，模型一在支座纵向活动方向承担了部分水平力，减小了主塔的纵向受力，在横向活动方向支座的水平刚度减小了横向固定的盆式支座水平剪力，有利于保护横向固定支座不被剪坏;模型二的纵向水平力全部由桥塔承受，横向水平力则由横向固定支座及桥塔承受。

⑤大跨度斜拉桥在地震作用下的梁端及塔顶位移，横向位移基本相同，而对于纵向位移，不考虑支座影响的模型二的位移量是考虑支座影响的模型一的位移量的3倍。

⑥在E1地震动作用下，采用弹簧单元模拟的盆式支座活动方向临界滑动摩擦力Fmax=μdR的计算结果小于弹簧单元的水平剪力，表明主梁与盆式支座活动方向发生相对滑动，因此活动盆式支座不能采用规范推荐的双线性理想弹塑性弹簧单元来模拟，即在E1地震作用下应不考虑支座的影响来建立全桥模型模拟在地震作用下的反应谱响应。

5 结束语

(1)考虑活动支座影响的斜拉桥模型比不考虑活动支座影响的模型基本振动周期短、刚度大，两模型之间前4阶自振模态变化大，第5阶之后的振型基本相同。

(2)考虑地震作用下支座的影响，能够减小盆式支座固定方向的水平力，也能减小桥塔根部截面的剪力和弯矩，但增加了其他桥墩墩底的内力。因此在设计时应平衡考虑上部结构和下部结构之间的受力关系，在确保桥墩地震安全的前提下合理选用和布置支座，尽量减小桥塔的受力，保证主塔在大震作用下发生局部轻微损伤或不发生损伤。

(3)在小震作用下，盆式支座在活动方向受到的水平力小于临界滑动摩擦力，则需要考虑活动支座对全桥结构的影响。在大震甚至设计地震时，盆式支座的活动方向受到的水平力大于临界滑动摩擦力，应将支座活动方向的刚度完全释放。

(4)不考虑支座影响的斜拉桥结构，在地震作用下以纵漂振型为主，导致全桥纵向位移较大，需要采取相应的措施来减小全桥的纵向位移，防止主梁与附近桥跨发生碰撞损坏。

［1］王克海．桥梁抗震研究［M］．北京:中国铁道出版社，2006

［2］邹立华，王克海，赵人达．大跨RC斜拉桥的非线性地震响应分析［J］．铁道学报，2004，26(6):95 －99

［3］王克海，朱晞．斜拉桥基于模态分析的滑动状态减震控制研究［J］．桥梁建设，2001，6:1 －4

［4］范立础．桥梁抗震［M］．上海:同济大学出版社，1997

［5］孙利民，张晨南，潘龙，等．桥梁桩土相互作用的集中质量模型及参数确定［J］．同济大学学报，2002，30(4):409 －415

［6］戴鹏，郝宪武，狄谨．大跨径P斜拉桥地震响应非线性分析［J］．郑州大学学报(工学版)，2006，27(4):79 －83

［7］叶爱君，胡世德，范立础．斜拉桥抗震结构体系研究［J］．桥梁建设，2002(4):1－4