高铁桥墩沉降趋势预测

江 浩 王克晓 姜 涛 王 建 邢卫军

(1.铁道第三勘察设计院集团有限公司，天津 300142;2.天津铁道职业技术学院，天津 300240;3.莱钢集团鲁南矿业有限公司，山东临沂 276421;4.中诚国际海洋工程勘察设计有限公司，山东青岛 266071)

随着经济发展和城市化进程的加快，城市之间出现了越来越多的高速铁路(以下简称“高铁”)，高铁在我国的兴起，在客观上提出了如何保证高铁施工和使用过程中的安全问题。如果地表受力不均匀，在不均匀沉降达到极限指标以上时，就会危及高铁的安全运营，就会发生桥墩倾斜甚至桥梁倒塌等灾害，直接影响到国家财产安全。

为了确保这些高铁的安全使用，必须对高铁进行沉降监测，以确定其变形状态。高铁变形监测内容一般有沉降监测、水平位移监测和倾斜变形监测等。由于高铁墩台变形主要表现在沉降变形上，所以对高铁沉降进行监测是十分必要的。

1 沉降量预测的理论方法

(1)双曲线法

双曲线法是假定沉降平均速度以双曲线形式减少的经验推导法。该法对预测应力－应变关系明显呈非线性的高压缩性软黏土较为合适。该法可表示为

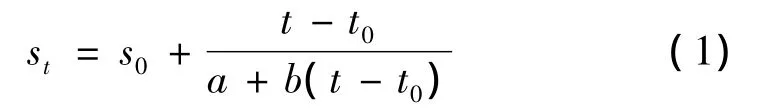
式中:s0为个曲线段初期沉降量;t0为初期监测时间。当t=∞时，最终沉降量可用上式求得

式(2)经变形后可得

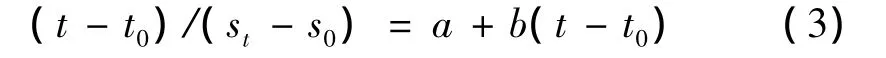
由上式可以看出，以t－t0为横坐标，以(t－t0)/(s－s0)为纵坐标建立坐标平面，取多组沉降实测值绘于该坐标平面内，拟合曲线即为一条直线，其斜率为b，截距为 a。

(2)卡尔曼滤波法

本文主要讨论动态测量系统卡尔曼滤波在测量中的应用。动态测量系统一般是由处于运动之中的一组地面点或空间点所构成。这些点的位置可看作时间t的函数。高程监测网是一维网，点的位置是高程;平面监测网是二维网，点的位置是平面坐标;三维地面网点或卫星的位置可以是空间坐标或大地坐标(大地经纬度和大地高)，为了估计动态测量系统的运动状态，通常是以点的位置和它们的运动速率为状态向量。设点i在时刻t的位置向量为ξi(t)，其瞬时速率为λi(t)，而将瞬时加速率Ωi(t)看作是一种随机干扰，即视为动态噪声。

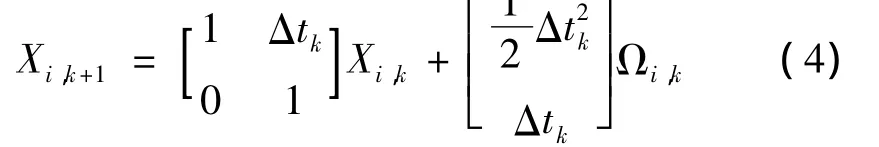
若记全网q个待定点的状态向量和动态噪声向量为

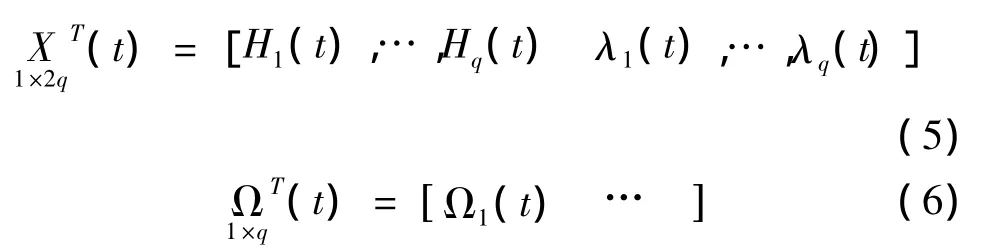
则经推算得到全网在第k+1期的状态方程

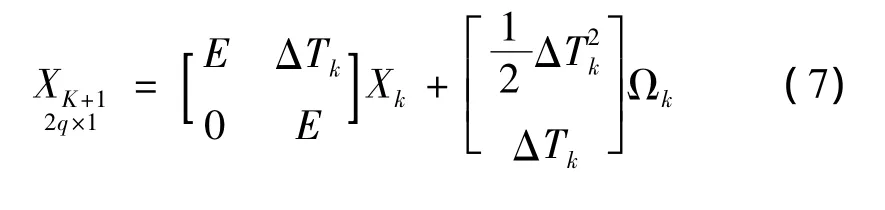
式中0，E，ΔTk均为 q阶方阵，且

如果认为第k+1期的观测高差都是在tk+1时刻观测的，则hij的观测方程为

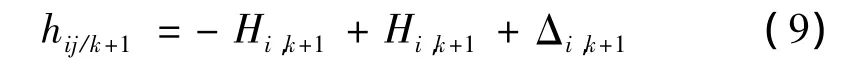
其形式与经典平差相同，如果各个观测高差的观测时刻tij/k+1不相同，设第k+1期的中心时刻为tk+1，则观测方程为

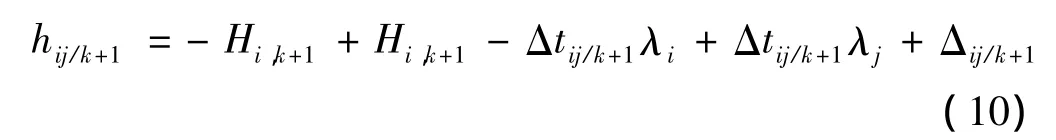
式中，Δtij/k+1= tij/k+1－tk+1。

2 变形监测的结果

监测点QDDXZ0428的具体沉降数据见表1和图1。

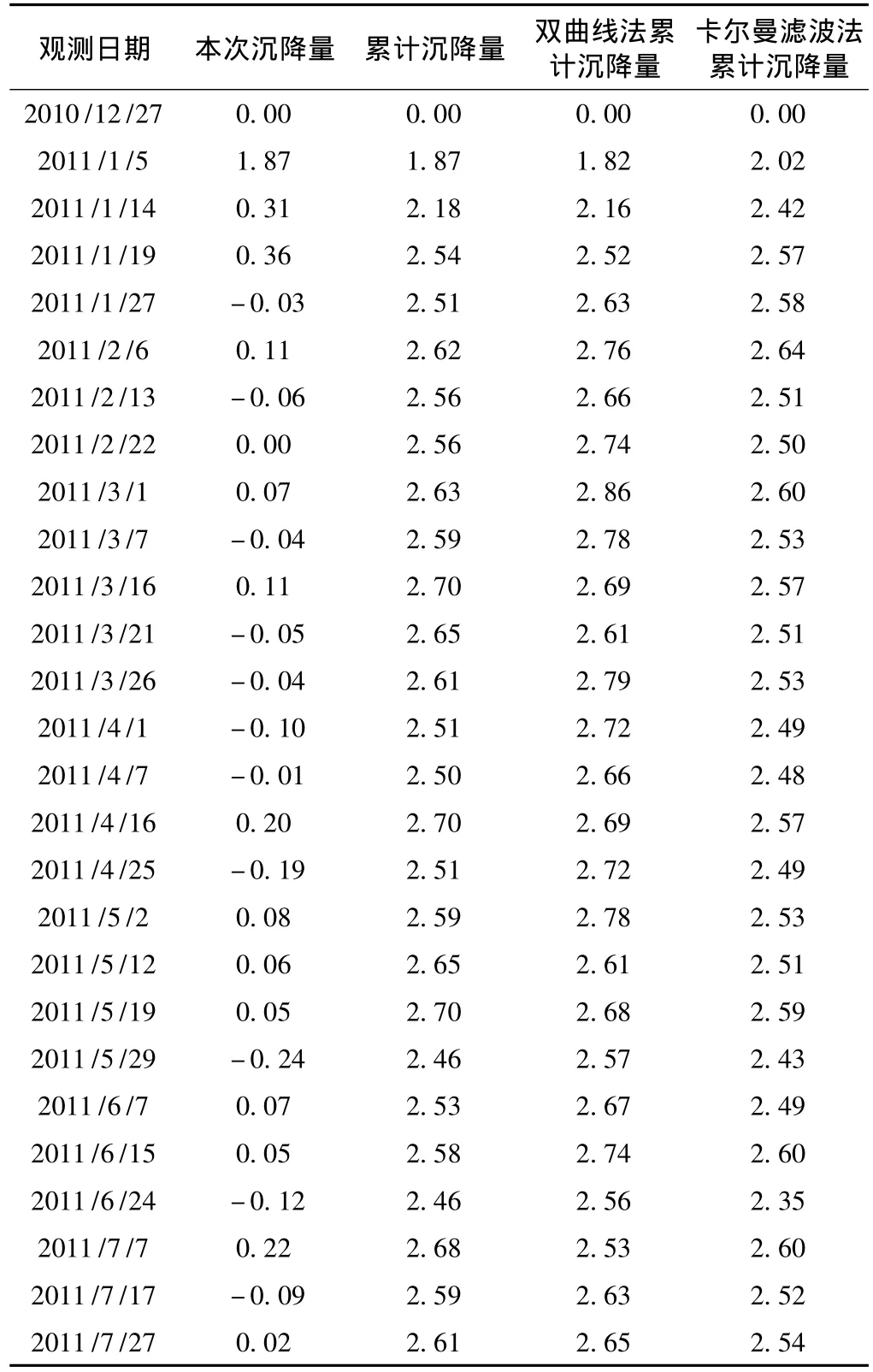
表1 桥梁墩(台)QDDXZ0428沉降量汇总 mm

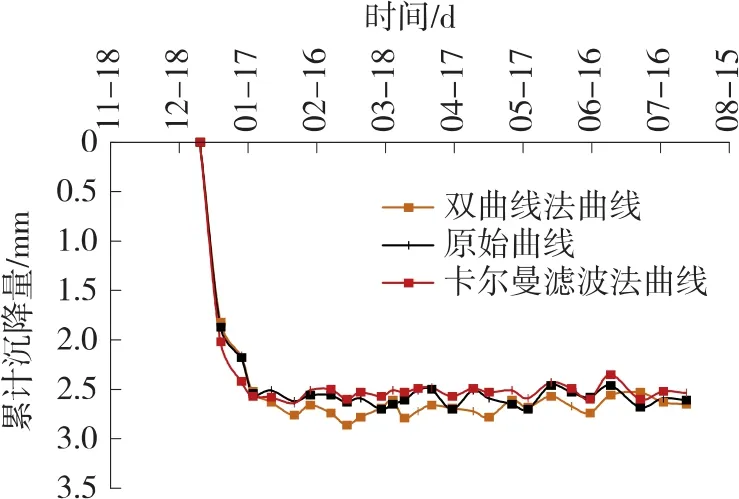
图1 QDDXZ0428时间－沉降量(预测沉降量)

其中绿色的曲线是利用双曲线法预测得出的沉降量曲线，红色的曲线是利用卡尔曼滤波法预测通过matlab软件得出的沉降量曲线，图上几乎水平的曲线是沉降速率曲线。由于曲线沉降量很小，所以沉降速率变化很小，几乎不变。也就是说利用卡尔曼滤波法预测沉降曲线与实际沉降曲线的变化趋势比较一致。在该地质条件下，该时间段中的沉降曲线利用卡尔曼滤波法比双曲线的方法预测得出的结果更好一些。针对于同一时间两种方法预测结果分别与原始检测值进行求差。从而更能明显地得出卡尔曼滤波法比双曲线法预测的结果更接近真实的检测值。

为了排除在桥墩QDDXZ0428点有巧合的情况发生，又随机选择桥墩QDDXZS0055点进行预测(如表2、图2所示)。

表2 桥梁墩(台)QDDXZS0055沉降量汇总 mm

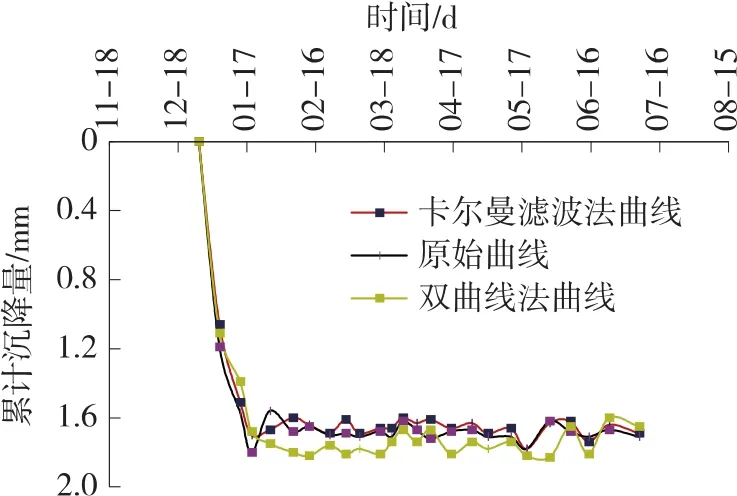
图2 QDDXZS0055时间－沉降量(预测沉降量)

从该点(桥墩QDDXZS0055)的实际沉降曲线与卡尔曼滤波法预测曲线(红色曲线)、双曲线法预测曲线(绿色曲线)这两种曲线的对比，可以得出与桥墩QDDXZ0428点一样的情况。从这两组曲线预测可以看出，只是在某些特殊的情况下稍微有些不符，在大多数的情况下卡尔曼滤波法预测的曲线基本上能与实际的变化曲线一致。从“荷载－时间－沉降量/沉降速率图”看，该评估单元整体沉降趋于稳定，自评满足客运专线无碴轨道铺设条件，可以进行下一步施工。

3 结论

双曲线法是假定沉降平均速度以双曲线形式减少的经验推导法，所以该法对预测应力－应变关系明显呈非线性的高压缩性软黏土较为合适。卡尔曼滤波法是一组一组地推计算公式的方法，其计算过程是一个不断预测、修正的过程。在求解时不需要存储大量的观测数据，而且当得到新的观测数据时，可随时得到新的滤波值，便于实时处理观测成果。而高铁桥梁墩(台)上面的沉降点的动态变化是彼此不相关的，所以利用卡尔曼滤波法进行预测很有效。

［1］崔希璋，等．广义测量平差［M］．武汉:武汉大学出版社，2009

［2］张正禄，等．工程测量学［M］．武汉:武汉大学出版社，2005

［3］黄声享，尹晖，蒋征．变形监测数据处理［M］．武汉:武汉大学出版社，2003年．

［4］张福荣．自适应卡尔曼滤波在变形监测数据处理中的应用研究［D］．长安大学，2009

［5］刘建国．基于卡尔曼滤波的BP神经网络模型在桥梁形变中的应用［D］．西安:长安大学，2010

［6］岳建平，田林亚．变形监测技术与应用［M］．北京:国防工业出版社，2007

［7］岳建平，方露，黎昵．变形监测理论与技术研究进展［J］．测绘通报，2007(7)

［8］吴涛．客运专线隧道线下工程变形监测信息管理及预测系统研究［D］．长沙:中南大学，2009