机车高圆簧的有限元分析

2012-11-27王生武李晓苏吴昌华

铁道机车车辆 2012年4期

王生武，李晓苏，吴昌华

（大连交通大学，辽宁大连116028）

随着铁路向着高速、重载方向的快速发展，机车车辆的动力学性能越来越被重视，对车辆运行品质的要求也越来越高。机车车辆悬挂系统参数和轨道系统参数等对机车车辆动力学性能、曲线通过性能及运行稳定性等具有重要的影响。作为机车上的二系悬挂装置，因其具有良好的减振效果等优势，在现代机车车辆上得到广泛应用，是决定机车动力学性能的重要构件之一，因此高圆簧的力学分析计算也是一个重要内容。

然而，在高圆簧生产和开发的设计计算中，其刚度计算等至今仍然沿用材料力学的简化计算方法，或者是直接依靠工程经验来完成。这种方法的计算模型是将弹簧看成等截面弹性直杆，再利用试验数据确定修正系数，完全忽略了高圆簧的实际结构、上下端弹簧丝几何形状的变化［1-2］。另一方面在计算中仅仅考虑计算剪应力，但当机车运行过曲线时，高圆簧要承受很大的弯矩，法向应力值相当可观。近年来出现了用有限元法算法，但由于在分析中没有考虑上下两端的橡胶垫板的接触非线性、弹簧变形的几何非线性等力学非线性问题，计算结果仍不太理想。本文使用ABAQUS软件，在考虑上述各类非线性问题的条件下，模拟机车通过曲线等各种真实工况，对高圆簧进行了分析。

1 高圆簧的计算

1.1 高圆簧的材料力学方法计算

材料力学对一般弹簧的计算原理是将弹簧丝近似看成等截面直杆来进行分析，由此得到高圆簧的纵向变形量λ及刚度C。

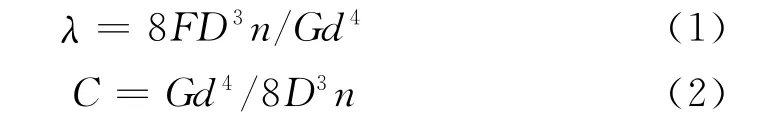
式中D，d分别是簧圈直径和簧丝直径；n是弹簧有效圈数；G是剪切弹性模量；F是弹簧所承受的轴向力。

在计算剪切应力时引进曲率（k）的影响，按式（3）计算：

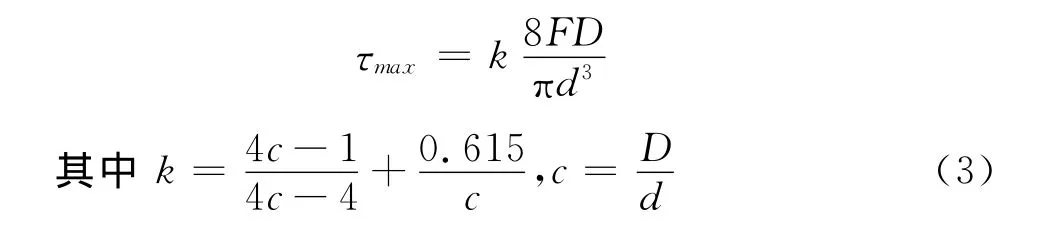
图1 高圆簧实体模型

图2 高圆簧有限元模型

但该方法未考虑法向应力。

本文取某机车二系悬挂的高柔度等截面螺旋压缩弹簧为研究对象，形状如图1所示。弹簧的总圈数9，有效圈数7.5，弹簧直径244mm，簧丝直径48mm，自由高645mm。F=73.5kN，E=200GPa。用材料力学方法计算的结果列于表1。

表1 高圆簧参数的传统方法计算结果

1.2 高圆簧的有限元计算

Pro／E环境下生成弹簧的实体模型见图1。模型中除满足2.1中所述的技术参数外，对模型进行了进一步的细化处理。除支撑圈外各圈簧距均等，两端最后一圈簧距逐渐变小，直至支撑圈端部与第2圈接触；弹簧两端支撑圈水平切削后磨平，支撑圈端部厚度不大于簧丝直径的1／4；端部簧丝水平切削部分长度不小于单位簧圈的3／4，从而使其与真实情况一致［3-4］。

为研究不同单元类型对计算精度的影响，分别选用6面体8节点等参数元素（简称参元）及六面体20节点等参元对弹簧进行离散。考虑弹簧两端支撑圈被切削后簧丝形状不规则，两端采用4面体单元离散模型。图2为高圆簧的网格划分模型。本文计算模型中单元边长约为5mm，最小单元边长为2mm，单元总数为253 000。

根据工况弹簧下端支撑圈的端面施加全约束，并对上端支撑圈的端面通过节点位移的耦合约束实现上端面保持水平。在上端面施加轴向均匀载荷，当载荷加到一定程度时支撑圈与第一个工作圈的簧丝间将产生接触，从而使问题变成几何非线性与边界非线性的双重非线性问题。根据实际工况，设轴向力F为73.5kN，材料弹性模量E=200GPa，泊松比μ=0.3。计算结果如表2所示。

表2 高圆簧参数的有限元计算结果

计算结果表明，用20节点与8节点单元模型得到的轴向位移及刚度（刚度C=F／λ）基本一致，虽然从理论上看，20节点等参元比8节点等参元精度更高，但由于网格划分得足够密，不同单元类型对本算例计算结果影响不大。因此，在高圆簧的计算中基于计算工作量的考虑，可选取6面体8节点等参单元类型为最终使用的有限元计算单元。

1.3 有限元计算与理论计算结果的比较及分析

分别对高圆簧模型进行材料力学理论算法和有限元方法的计算，其结果如表3所示。

表3 高圆簧材料力学计算与有限元计算的比较

图3 轴向位移云图

图4 切应力云图

从有限元计算结果看，对于簧丝上指定的横截面而言，剪切应力从簧丝中心至边缘逐渐增大，这与材料力学的结果一致。但是，对于整圈弹簧而言其不同横截面上的应力大小不同，而且每圈簧上最大切应力点的连线大致构成一条与轴线平行的直线。当簧圈压死时，相互接触的两簧圈切应力分布完全不同（图4）。所有这些规律用材料力学理论均无法反映出来，同时也没有弹簧法向应力的描述，但是有限元计算显示出高圆簧受力时存在着相当大的法向应力。可见对于大轴功率和恶劣条件下运行的机车，其高圆簧的强度计算不应忽略法向应力的重要影响。

2 橡胶垫对高圆簧特性的影响

2.1 轴向压力下高圆簧的力学分析

作为机车二系悬挂装置的高圆簧，弹簧两端均串联橡胶垫，本文建立了高圆簧与两端橡胶垫的一体模型，按照图纸技术要求给定橡胶垫的弹性模量Ex=10 GPa，泊松比μx=0.45。载荷同1.1节所述。用接触问题模拟弹簧簧丝间的关系，来分析橡胶垫对高圆簧特性参数的影响。为计算结果的比较分析，还考虑了弹簧两端串联刚性板的情况。其计算结果如表4所示。

表4 ABAQUS环境下高圆簧有限元计算

图5 高圆簧的法应力云图

图6 法应力截面图

计算过程显示，当开始施加轴向载荷时，弹簧第一圈与第二圈之间也开始发生接触，随着载荷量增加，接触面积逐渐增大，直至载荷增至73.5kN，第一圈约有3／4簧圈与第二圈接触。

在无垫板、刚性垫板和橡胶垫板的3种条件下，横截面剪应力的大小、分布规律基本一致，而且高圆簧位移和刚度的计算结果均基本一致。值得强调的是高圆簧承受载荷时存在法向应力，其最大法应力发生在第3个有效圈上，而且法应力沿簧丝中心位置到簧丝边缘位置逐渐增大，如图5、图6所示。进一步比较3种条件下的结果可知，两端串联橡胶垫的高圆簧相比两端串联刚性板的高圆簧法应力要小，表明橡胶垫降低了法向应力，这与文献［6］的结论一致。

2.2 有水平位移时高圆簧的力学分析

当机车运行特别是过曲线时，高圆簧要承受很大的弯矩。为模拟真实的极限工况，本文以轴向力与横向位移载荷共同作用的方式来模拟机车的曲线通过。在对高圆簧施加73.5kN垂向载荷的同时，再施加最大89.4mm的水平位移。计算结果列于表4，图7～图10为高圆簧两端串联橡胶垫时的位移与应力云图。

与只施加轴向载荷的情况相比，同时施加轴向压力和水平位移时，高圆簧垂向位移减少，减少部分用来协调水平方向上的位移变量；从剪应力云图上看，截面剪应力较只施加轴向载荷时增加了12%，最大应力值发生在上端第2个有效圈的簧丝内侧。另外，比较图4和图8结果可知，由于横向位移的影响整个弹簧的剪应力在左右部分分布不对称，而材料力学无法得出这些现象。法应力较只施加轴向载荷时有很大的增加，最大法应力发生在弹簧第2个有效圈上；由于横向位移载荷的影响，弹簧每圈的最大法应力产生部位，由上至下环绕弹簧轴线方向扭转，如图9所示。