基于法向应力突变的抗滑桩土拱效应数值分析

王　诚，石少卿，储召军

(后勤工程学院 军事土木工程系，重庆　401311)



基于法向应力突变的抗滑桩土拱效应数值分析

王诚，石少卿，储召军

(后勤工程学院 军事土木工程系，重庆401311)

摘要：土拱效应是抗滑桩与土相互作用的重要现象之一，应用有限元软件，采用区别于常规方法的法向应力突变的方法分析埋入式抗滑桩桩后土拱效应，研究了桩后土拱效应发生机理，分析了桩间距、土体参数、荷载等影响因素对桩后土拱效应的影响，并结合桩土荷载分担比作了对比分析；分析表明：桩间距对桩后土拱效应影响非常显著。

关键词：抗滑桩；土拱效应；有限元；法向应力

土拱效应是土体发挥自身抗剪强度，产生土体内应力重分布，将作用在土拱上的压力传递到桩身、通过抗滑桩传递到稳定的岩土层中的一种应力迁移现象，广泛存在于岩土工程中。Terzaghi于1943年通过活动门试验证明了土拱效应存在[1]，此后Liang[2]、张建勋[3]、申永江[4]、刘金龙[5]、李志雨[6]利用有限元软件分析了土拱效应的形成机理与发展规律，探讨了桩间距、桩排距、土体参数等因素对土拱效应的影响。传统的分析方法多采用计算桩土荷载分担比进行分析，但不适用于不存在桩前土的悬臂式抗滑桩，存在一定的缺陷。董捷[7]针对悬臂式抗滑桩，提出利用土拱拱顶的法向应力突变效应判断土拱效应。本文是在前人的基础上，应用有限元软件ANSYS，采用法向应力突变的方法研究桩间距、土体性质参数、荷载等因素对埋入式抗滑桩桩后土拱效应的影响，并与采用桩土荷载分担比的方法做了对比分析。

1基于法向应力突变的土拱效应理论

桩后水平土拱效应是以抗滑桩作为拱脚，将桩间的推力等外部荷载转化为拱脚轴力的现象，董捷[7]针对悬臂式抗滑桩，提出了利用土拱拱顶的法向应力突变效应判断土拱效应的方法。

本文主要研究埋入式抗滑桩的土拱效应，由于有桩前剩余抗滑力和桩前土作用分担了部分滑坡推力，作用于抗滑桩背侧的推力应小于滑坡推力，所以常规方法中土拱效应可以通过桩土承载荷载分担比的大小反映。

由土体抗压不抗拉的特点，假定土拱拱型为合理拱轴线，合理拱轴线上任意一截面上没有拉力和弯矩，只有压力，如图1所示，其中土拱跨度l，拱高为f，等效土拱厚度为t,合理拱轴线方程为

单位高度的跨中截面(x=l/2)的轴力为

图1　土拱受力示意图

因此，可以利用法向应力突变程度衡量土拱效应的作用程度和范围，本文基于此理论进行了数值模拟分析。

2有限元模型的建立

2.1问题简化

土拱效应事实上是空间问题，但是Chen[8]通过有限元软件模拟了抗滑桩与边坡土体的相互作用，对比二维、三维桩间土体位移图发现采用平面应变问题能较好模拟三维状况下的桩土相互作用问题，此后很多研究人员将桩土相互作用问题简化成二维平面应变问题，为研究带来方便。在前人研究基础上，选取地表以下一定深度的单位厚度土层作为研究对象，简化为二维问题，并假定土层位移限定在水平方向，同时桩体水平位移为零。

3.2基本算例

采用桩径d=1m，桩的中心距s=5m，作用在土体上的均布荷载p=10kPa，土层采用粘性土，一般抗滑桩前后计算区域取大于10d，为明确桩后土拱效应的影响范围，本文取15m，简化后的计算模型如图2所示，计算参数见表1。土体采用Drucker-prager模型，桩与土设置接触对，土体的左右边界采用x向约束，土体前侧边界采用y向约束。

图2　桩后土拱效应的平面简化模型

弹性模量E/kPa泊松比ν粘聚力c/kPa内摩擦角φ/(°)膨胀角ψ/(°)土体30000.310250桩2×1070.2

3土拱效应机理与影响因素分析

3.1桩后土拱作用机理

在土体后侧边界施加均布荷载后，计算得到位移云图如图3所示，主应力矢量图如图4。由位移云图可以看出在抗滑桩前土体内形成了显著的位移拱，抗滑桩后土体内主应力方向发生偏转，形成了应力拱。事实上，土拱效应是土体颗粒间的剪应力和法向应力使桩间土体挤压，产生相对位移，使颗粒间互相“楔紧”，将拱上土压力转为轴力再传至拱脚的过程，只有桩与土体之间发生相对位移或相对位移趋势时才会产生土拱效应。由图3可见桩间土体与桩产生相对位移，之后由图4可见主应力方向发生偏转，形成大主应力拱。

图3　土体位移云图

图4　主应力示意图

由对称性，两抗滑桩各选取一半，作出两桩中心连线上不同点的法向应力σx与y方向应力σy变化曲线，如图5，图6。

由图5可以看出，桩中心连线上桩后土体内法向应力发生突变，由前述理论可知在该法向应力突变区域发生了明显的土拱效应，其中在桩后1.7 m处法向应力σx达到最大；距抗滑桩较远处法向应力变小且没有突变，说明距桩较远处土拱效应较弱或没有土拱效应发生；土拱前的法向应力σx迅速下降，这是由于发生土拱效应，桩间土压力转移到作为拱脚的抗滑桩上导致的，在应力分布上反映了桩后土拱的挡土作用。由法向应力突变区域大致判断桩后土拱效应作用区域为抗滑桩至桩后2.8 m之间。

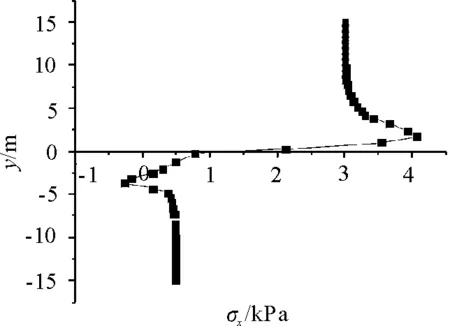
图5　桩中心连线上的法向应力σx分布曲线

图6　与x轴垂直的不同剖面σy分布曲线

由图6可以看出，距离抗滑桩较远处，土体y方向的应力σy分布较均匀，距离抗滑桩较近时，σy在桩后较大，桩间较小，呈现中间高两边低的形状，这也反映出桩后土体应力转移至抗滑桩上，发生了土拱效应。进一步计算出桩前3m的σy曲线与x=0、x=5、σy=0所围成的区域面积即该曲线位置的截面上承担的荷载，算得抗滑桩桩前土体承担的荷载为8.57kN/m，施加的总荷载10kPa×5m=50kN/m，即土的荷载分担比为17.1%，桩的荷载分担比为82.9%。

结合图5、图6分析，两图均表明桩后的土体应力发生迁移，桩后土体产生了土拱效应。

3.2桩间距对土拱效应的影响

桩间距取值是当前抗滑桩设计的一个关键问题，桩间距取值过大，大于某一临界值时，桩后土拱效应较弱或没有发生土拱效应，不能充分利用土体的抗剪强度将荷载转移到桩上，同时桩间距过大，桩的挡土作用不明显，土体可能会从桩间挤出；桩间距过小时，造价较高，不够经济。大量研究表明桩间距是影响抗滑桩桩后土拱效应的主要因素，同时也受到抗滑桩桩径的影响，为了具体分析桩间距对桩后土拱效应的影响，其他参数不变，桩间中心距s分别取为2，3，5，8，10，由桩径d=1得s/d分别为2，3，5，8，10，作出各组情况下的两桩中心连线上的不同点的法向应力σx曲线如图7所示。

同时作出桩前3m不同点的y方向应力σy变化曲线，计算σy曲线与x=0、x=5、σy=0所围成的区域面积即土体承担的荷载，进一步算得土的荷载分担比、桩的荷载分担比，如图8所示。

图7　桩中心连线上的法向应力σx分布曲线

图8　不同s/d时的桩土荷载分担比

由图7可以看出，在不同的s/d情况下，抗滑桩桩后土体的法向应力均发生突变，即桩后均发生了土拱效应。桩间距较小时，法向应力突变非常显著，如s/d=2时桩后法向应力由3kPa陡增至4.7kPa，s/d=3时桩后法向应力由3kPa陡增至4.3kPa，随着桩间距的增大，桩后法向应力突变程度减弱，s/d=8时桩后法向应力由3kPa增大至3.8kPa，s/d=10 时桩后法向应力由3kPa增大至3.7kPa，其突变的幅度基本不再增大甚至有所减小，同时法向应力发生突变的区域向桩后推移表明桩后土拱效应减弱，抗滑桩的挡土作用不明显。

由图8可以看出随着s/d的增大，桩的荷载分担比越来越小，土的荷载分担比越来越大，s/d=8时，桩的荷载分担比减小趋势和土的荷载分担比增大趋势明显加快。

综合图7、图8，采用法向应力突变方法和计算桩土荷载分担比的方法均可看出，s/d较小时，土拱效应较明显，s/d大于8时，抗滑桩的挡土作用不明显，桩后土拱效应减弱。因此可以认为桩间距为2～8倍桩径时，桩后土拱效应较明显，这与文献[9]的分析结论一致。

3.3土体性质对土拱效应的影响

研究表明：土体性质对土拱效应会产生一定的影响，其余参数不变，只改变土体的粘聚力、内摩擦角、弹性模量，采用两种方法分析对土拱效应的影响。土体粘聚力C=10kPa，仅改变土体内摩擦角φ，作出两桩中心连线上的不同点的法向应力σx曲线，如图9所示。同时计算出不同内摩擦角φ时桩的荷载分担比，如图10所示。

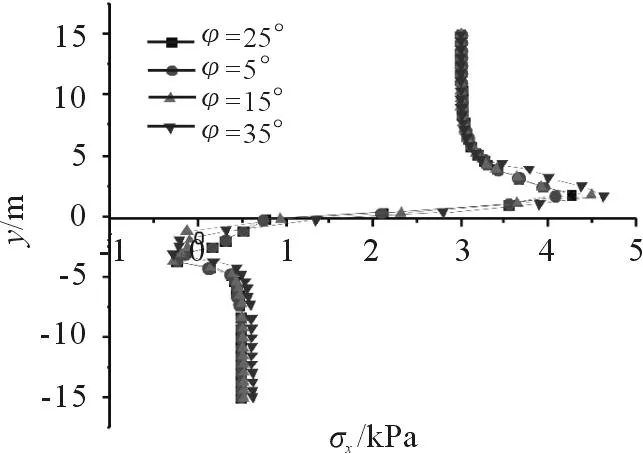
图9　不同内摩擦角φ时法向应力σx曲线

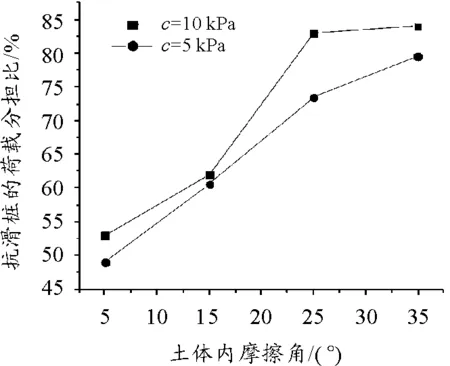
图10　不同内摩擦角φ时桩的荷载分担比

由图9可以看出，不同内摩擦角φ时，桩后法向应力均发生了突变，均发生了土拱效应。φ越大，法向应力发生突变的区域更大，突变幅度也更大，表明在该区域内土体应力更多的通过土拱作用迁移到桩身上，土拱效应越显著。由图10可以看出，土体内摩擦角φ增大，桩的荷载分担比增大，同样表明土体应力更多地迁移到桩身上，土拱效应更显著，且土体粘聚力c较小时，该规律更明显。

取内摩擦角φ=25°，改变土体的粘聚力c，作出不同情况下的法向应力曲线如图11所示。同时计算出不同粘聚力c时桩的荷载分担比，如图12所示。

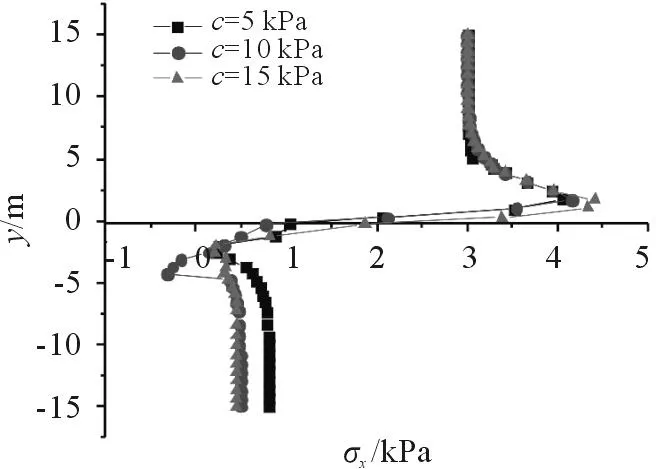
图11　不同粘聚力c的法向应力σx曲线

图12　不同粘聚力c时桩的荷载分担比

由图11可以看出，不同粘聚力c时，桩后法向应力均发生了突变，均发生了土拱效应。c越大，法向应力发生突变的区域更大，突变幅度也更大，表明在该区域内土体应力更多的通过土拱作用迁移到桩身上，土拱效应越显著。由图12可以看出，随着粘聚力c增大，桩的荷载分担比增大，同样表明土体应力更多地迁移到桩身上，土拱效应更明显，这与文献[10]的结论一致。

3.4不同荷载对土拱效应的影响

为探究荷载对桩后土拱效应的影响，分别取外部荷载为10 kPa、20 kPa、30 kPa，50 kPa，作出各组的两桩中心连线上的不同点的法向应力σx曲线，如图13所示。算得各组荷载下的抗滑桩的荷载分担比，如图14所示。

图13　不同荷载下的法向应力σx曲线

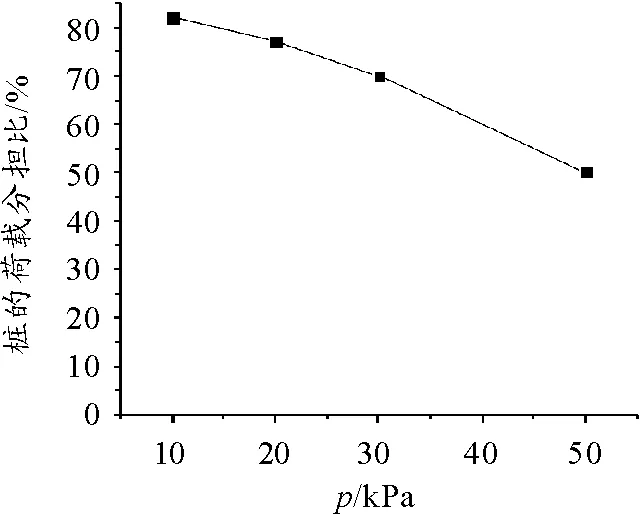
图14　不同荷载时桩的荷载分担比

由图13可以看出，荷载较小时，随着荷载的增大，桩后相同位置的土体应力随着荷载的增大而增大，桩后土体的法向应力均发生了突变，且突变幅度有所增大，表明土拱效应有所增强。这是因为土拱效应是土体受挤压产生楔紧作用，抗剪强度发挥，内部应力重分布，将荷载转移到桩身上的过程。随着荷载的加大，土体挤压得更加密实，更好的发挥了土体的抗剪强度，土拱效应有所增强。当荷载增大到50 kPa时，桩后土压力发生了突变，但远离抗滑桩的位置土压力波动明显，表明桩后土拱效应减弱，土体的应力分布发生改变。这是由于随着荷载进一步增大，土拱形状产生变化，土体内应力分布更趋复杂，土拱的稳定性变弱，土拱效应减弱，当荷载超过土拱的承受能力时，土拱发生破坏。对比不同荷载时桩的荷载分担比可以看出，荷载较小时，桩的荷载分担比变化不大，当荷载很大时，桩的荷载分担比迅速下降，这是由于荷载增大到一定程度后，土拱产生一定程度的破坏，土拱效应减弱，土体不能将荷载更多地传递到桩身上导致的。

4结论

本文采用二维有限元的数值模拟方法，对抗滑桩的桩后土拱效应进行模拟，应用法向应力突变的分析方法可以有效地对土拱效应进行分析评价，并结合桩土荷载分担比的方法进行对比，初步得出以下结论:采用分析法向应力突变的方法来衡量土拱效应的作用程度和范围是可行的；桩间距对抗滑桩桩后土拱效应影响明显，当桩间距在2～8倍桩径时，法向应力突变明显，桩间土拱效应较显著，随着桩间距的增大，桩的荷载分担比不断减小；土体的粘聚力和内摩擦角越大，法向应力突变越明显，桩的荷载分担比不断增大，土拱效应越显著；在土拱的承载能力范围内，随着荷载的增大，法向应力突变越显著，土拱效应增强，超出范围后再增大荷载，法向应力分布很不规律，土拱效应减弱甚至消失。采用法向应力突变的分析方法仅需作出法向应力曲线，即可根据土压力突变来判断桩后土拱效应的作用范围和程度，可进一步将该方法应用于土拱效应模型试验分析中。

参考文献：

[1]TERZAGHI K. Theoretical soil mechanics[M].New York:John Wiley & Sons，1943.

[2]LIANG R，ZENG S.Numerical study on soil arching mechanism in drilled shafts for slope stabilization[J].Soil and Foundation，2002.42(2)：83-92.

[3]张建勋，陈福全，简洪钰.被动桩中土拱效应问题的数值分析[J].岩土力学，2004，25(2)：174-178,184.

[4]申永江，杨明，项正良，等.双排桩桩间土拱效应的发育规律研究[J].水文地质工程地质，2015，42(1)：70-74.

[5]刘金龙，王吉利，袁凡凡.不同布置方式对双排抗滑桩土拱效应的影响[J].中国科学院研究生院学报，2010，27(3)：364-369.

[6]李志雨，何晖，郭智.基于桩间土拱效应的微型桩间距的分析[J].山地学报，2015,33(3)：326-330.

[7]董捷，张永兴，文海家，等.悬臂式抗滑桩三维土拱效应研究[J].工程勘察，2009(3)：5-10，30.

[8]CHEN C Y，MARTAIN G R.Soil-structure interaction for landslide stabilizing piles[J].Computer and Geotechnics，2002，29(5)：363-386.

[9]石胜伟，梁炯，韩新强，等.微型组合抗滑桩距径比的模型试验[J].地质通报，2013,32(12):2008-2014.

[10]吴昌将，张子新.边坡工程中抗滑桩群桩土拱效应的数值分析[J].地下空间与工程学报，2007，3(7)：1305-1309,1333.

(责任编辑周江川)

本文引用格式：王诚，石少卿，储召军.基于法向应力突变的抗滑桩土拱效应数值分析[J].兵器装备工程学报，2016(4):160-164.

Citation format:WANG Cheng, SHI Shao-qing, CHU Zhao-jun.Numerical Analysis of Soil Arching Effect in Passive Piles Based on the Mutability of Normal Stress[J].Journal of Ordnance Equipment Engineering,2016(4):160-164.

Numerical Analysis of Soil Arching Effect in Passive Piles Based on the Mutability of Normal Stress

WANG Cheng, SHI Shao-qing, CHU Zhao-jun

(Department of Civil Engineering, Logistic Engineering University, Chongqing 401311, China)

Abstract:Soil arching effect is one of the important phenomena in interaction of anti-slide piles and soil. By using the FEM software and a new method of the mutability of normal stress, the occurrence of soil arching effect and the effects of factors on the soil arching effect such as distance of piles, soil properties and the load were studied. Meanwhile, a comparative analysis of load-bearing ratio was made. It concludes that the distance of piles plays an important role in soil arching effect.

Key words:anti-slide pile; soil arching effect; finite element; normal stress

文章编号：1006-0707(2016)04-0160-05

中图分类号：TU43

文献标识码：A

doi:10.11809/scbgxb2016.04.038

作者简介：王诚(1991—)，男，硕士研究生，主要从事防灾减灾研究。

收稿日期：2015-09-23；修回日期：2015-10-29

【基础理论与应用研究】