基于谱的海浪模拟与谱估计＊

（中国人民解放军91550部队91分队 大连 116023）

1 引言

掠海飞行器飞行时，需要实时判断浪高来控制自身的飞行高度，过高会失去隐蔽性能，过低则有提前触浪入水的风险。因此在系统的仿真阶段，就需要考虑海浪对飞行性能的影响［1］。本文正是基于某掠海飞行器系统仿真的需要，研究海面浪高数据的实时模拟方法。

海浪模拟是在保证相对真实的情况下，简化模型模拟的复杂度，使复杂的海洋情况在虚拟的环境中得以再现。基于波谱的海浪模拟应用了波能谱理论，将海浪视为由多条波幅、频率完全不同的简谐波叠加而成，通过初相位随机选择反应海浪的随机性，以此为基础建立一个能真实反应海浪变化情况的数学模型［2］。文中通过已有的波谱函数，模拟海浪相对于海平面的高度，并通过模拟的数据反推波浪谱，与靶谱进行比较分析，证实该方法是可行的。

2 基于波谱的波面模拟

2.1 海浪数学模型

根据随机过程理论，可用无限个随机的余弦波的叠加来描述某一定点波面，其基本的数学模型如式（1）：

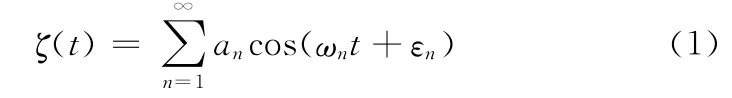
式中εn是0～2π区间内均匀分布的随机相位；an，ωn是组成波的振幅和圆频率。

在研究海浪的特征时，通常是对它进行谱分析。所谓谱分析就是阐明海浪的能量相对于波浪频率、波浪传播方向等其他独立变量的分布规律，建立函数关系。对式（1）所表示的波面，它所具有的能量可表示为：，ρ表示海水的密度，g为重力加速度。定义一个ω的函数：

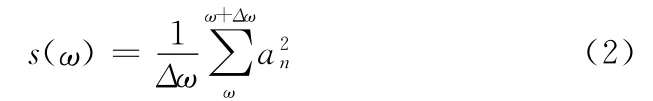
显然s（ω）与波面在间隔Δω内的平均能量成正比，可以将它等价为波浪的能量密度，它就是海浪仿真研究的核心，即海浪谱。当Δω趋近于无限小时，在Δω区间内的波趋于确定频率的谐波，上式变为：，得式（3）。该式即计算波面即时高度的数学模型。

2.2 海浪的模拟

海浪谱是窄带谱，频率很低和很高的简谐波对波幅的影响不大，只需选取具有代表性的一段频率进行仿真，就可以满足精度要求。确定端频率的规则为：s（ω）｜ω＝ω1＝ω2＝as（ωm），ωm为谱峰频率，ω1、ω2为端频率，由a的取值来决定。频谱离散化时，文中频率的划分采用等分法，即：Δω＝（ω2-ω1）／m，ωi＝ω1＋（ω2-ω1）（i-1）／m。文中靶谱选择P-M 谱，是Moscowitz于1964年对北大西洋上1955～1960年的观测资料进行460次谱分析求得的，它代表充分成长的风浪，在海浪研究及相关的工程问题中得到广泛运用。P-M 谱如式：

式中α＝8.1×10-3，β＝0.74，U为海面19.5m 高度处的风速，通过海况由表1确定。

表1 风浪海情关系表

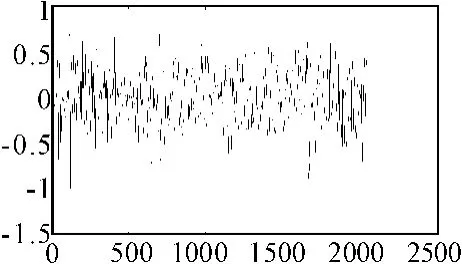
图1 定点波面模拟图

3 利用仿真数据估计海浪功率谱

3.1 功率谱估计

功率谱估计利用给定的一组样本数据估计一个平稳随机信号的功率谱密度，它能给出被分析对象的能量随频率的分布情况，因此被广泛的应用于雷达、声纳、地震等领域［6］。

功率谱估计可以分为经典谱估计和现代谱估计两大类。Welch方法是一种改进的周期图谱估计方法，属于经典谱估计。现代功率谱估计法大致分为参数模型谱估计和非参数模型谱估计两大类。最常用的模型有ARMA 模型、AR 模型、MA 模型，因其能提高信号的分辨率而得到广泛应用［7］。Matlab是一个强大数值计算软件，其语言简洁紧凑，运算丰富，具有强大的图形功能。文中利用仿真所得数据，通过Matlab6.5经典和现代功率谱估计函数进行功率谱估计。

图2 经典谱估计结果

图3 现代谱估计结果

经典谱估计采用Matlab函数pwelch（），结果如图2所示。现代谱采用AR 模型，阶数为4，结果如图3所示。从图中可以看出，图3的谱峰明显高于理论值，图2更接近理论波形。

3.2 谱估计结果分析

从图2、图3可以看出，仿真海浪谱大体反映了理想海浪谱形状。设仿真海浪频谱估计为＾s（w），理想海浪谱为s（w），根据仿真误差估计指标：

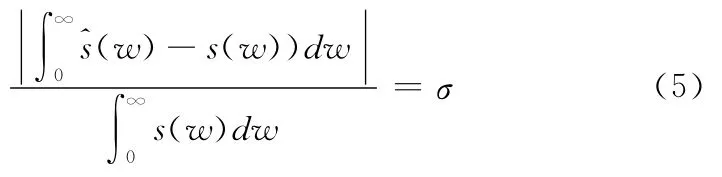
对经典谱估计结果和现代谱估计结果进行计算，得到仿真误差分别为：0.78%和1.48%，现代谱估计的误差大于经典方法估计结果。随着分割频段数的增加，经典谱估计结果将更接近理想海浪谱。

4 结语

本文描述了基于频率等分法进行海浪数值仿真的过程，首先通过风浪海情关系表确定海浪谱，然后进行海浪谱等频率间隔分割，确定波浪的频率成分，再根据采样时间间隔将各次谐波合成海浪仿真波形。文中最后利用现代谱估计方法和经典谱估计方法对仿真海浪数据进行频谱估计，并比较了两种谱估计方法的性能，验证该方法模拟波浪是有效的。本方法已应用于某系统仿真的海洋环境仿真中，是一种工程实用方法。

［1］张金春.基于海浪谱的东中国海海浪二维仿真［J］.海军航空工程学院学报，2008，23（2）：449-452.

［2］侯学隆.基于方向谱的海浪合成方法［J］.系统仿真学报，2010，22（1）：130-134.

［3］金文标，蒲鹏飞.基于频谱的海浪实时模拟［J］.重庆邮电大学学报，2009，21（3）：435-439.

［4］闫庆华.AR 模型功率谱估计及Matlab实现［J］.计算机与数字工程，2010，38（4）：154-156.

［5］何子述.现代数字信号处理及其应用［M］.北京：清华大学出版社，2009.

［6］陈海英.AR 模型功率谱估计常用算法的性能比较［J］.漳州师范学院学报（自然科学版），2009，63（1）：48-52.

［7］邱宏安.随机海浪模型的建立及仿真分析［J］.系统仿真学报，2000，12（3）：226-228.

［8］罗玉.基于海浪谱的3D海浪模拟［J］.武汉理工大学学报（交通科学与工程版），2008，32（2）：323-326.

［9］徐利明.基于谱分析的实时波浪模拟［J］.系统仿真学报，2005，17（9）：2092-2095.

［10］田宝国，耿霆.波浪力作用下无动力运载器水弹道仿真［J］.计算机与数字工程，2011，39（1）.

［11］丛滨.海浪模型的建立与仿真［J］.西安工业大学学报，2009，29（5）：475-478.