分数阶傅里叶变换的数值计算方法研究＊

（1.海军航空工程学院电子信息工程系 烟台 264001）（2.中国人民解放军91960部队 汕头 515074）

1 引言

对信号进行分数阶傅里叶变换（FrFT）可以解释为将信号坐标轴在时频平面绕原点逆时针旋转［1］。随着阶数a从0连续变化到1，表现出信号从时域到频域变化的全部特征，因此，可以看做是一种统一的时频变换。作为一维线性变换，可以有效地避免信号的交叉项干扰，具有较好的时频聚集性。因此，特别适合于线性调频信号（Chirp）的检测与参数估计［2］、时频滤波［3］、目标识别［4］等用途。

2 分数阶傅里叶变换定义

分数傅里叶变换算子Fa通过实变量a将函数x变换为Xa＝Fa（x），定义可以表述为整体积分变换：

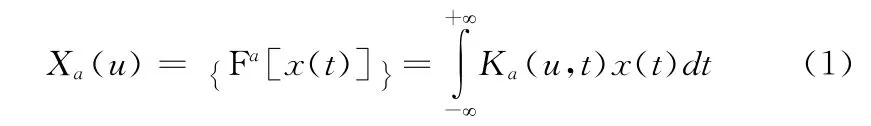
其中，a为FrFT 的阶数，u为分数阶域（FrFD），旋转角α＝a，则FrFT 变换核Ka（u，t）为

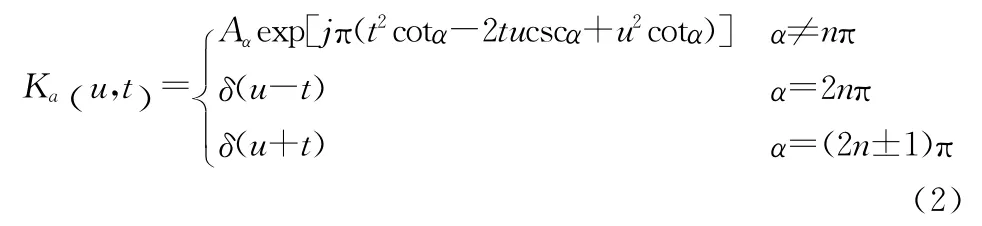
式中

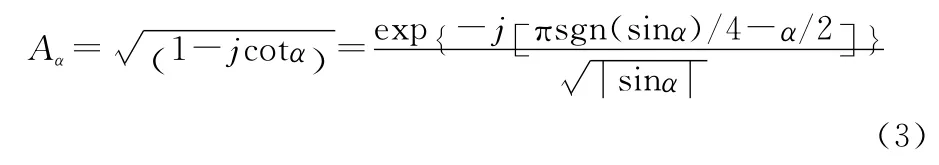
Xa（u）的逆变换为

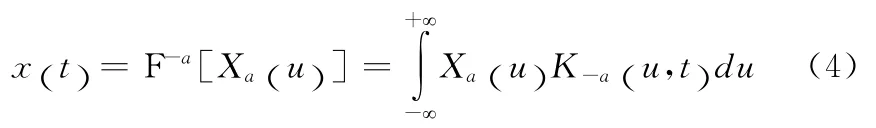
由上式可知，信号x（t）可以分解为一组系数为Xa（u） 的正交Chirp基K-a（u，t）的线性组合。

3 分数阶傅里叶变换数值计算

3.1 离散分数阶傅里叶变换定义

仿照离散傅里叶变换（DFT）的定义，x＝［x（0），…，x（N-1）］T的离散分数阶傅里叶变换（DFrFT）可以理解为x经过DFrFT算子Fa作用的结果［5］，即Xa＝Fax：

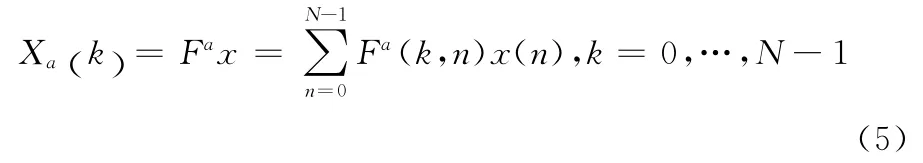
式中Fa（k，n）为DFrFT 核矩阵，Fa＝ΕΛaΕT，F＝ΕΛΕT为DFT 矩阵的特征值分解。

3.2 主要的数值计算方法

按照Fa（k，n）核矩阵的求法差异，我们可以将近年来主要的一些分数阶傅里叶变换的数值算法分为以下三类［6］：

1）特征分解型

特征分解算法通过求DFT 的核矩阵F（k，n）的特征值和特征向量构造DFT 核矩阵的分数幂，以此作为Fa（k，n）来计算DFrFT。Candan等在文献［7］中对DFrFT 进行了详细描述。S.C.Pei等在文献［8］提出了一种基于正交投影的特征分解型算法。此类方法的优点是保持了连续Fr-FT 的许多性质，但该法计算复杂度高，不能用来实时处理。

2）线性组合型

线性组合方法是对特定阶数的一些DFrFT 的线性组合来表示任意阶的DFrFT。文献［9］利用Taylor级数展开以及Caylay-Hamilton定理，将其表示为阶数为0，1，2，3的线性组合。虽然该方法计算量最小，但计算精度太低。文献［10］提出了另外一种DFrFT 线性组合型算法，将上述特殊阶数0，1，2，3变为从0阶开始间隔N／4取得N个阶数，其中N为样本个数。利用FrFT 的旋转相加性，可将一次变换的结果输入到后一次变换，因此算法可以采用串行的方法实现，可用超大规模集成电路（VLSI）实现。但缺点是，必须知道至少1个特定阶数变换的结果，同时这些阶数还与输入信号的样本个数N有关。

3）离散采样型

离散采样型算法实质上是，对连续FrFT 的输入输出信号进行采样获得DFrFT 核矩阵。由Ozaktas等学者提出的计算量与FFT 相当的快速近似分数阶傅里叶变换算法（FAFrFT），其本质是实现信号的离散取样值与连续FrFT的离散取样值之间的映射，计算复杂度仅为O（NlogN）［11］。该算法引起了国内外学者的广泛关注，使FrFT 从理论逐步走向工程实践，从而在信号处理领域得到广泛应用。具体步骤是：

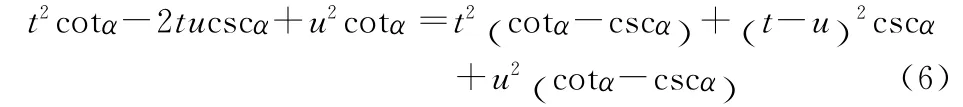
代入式（1），利用 （cotα-cscα） ＝-tan（α／ 2）化简得到：

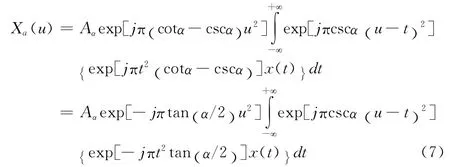
令Tr（x）＝exp（jπrx2），这里r可以取两个值v＝-tan（α／2），c＝cscα，定义算子g＝Tv·x，算子h＝Tc＊g。式（7）可以进一步简化为

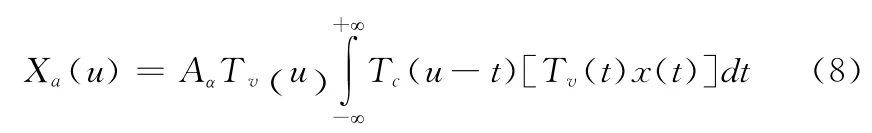
图1 FrFT 的1相实现原理图

这类算法将FrFT 分解为三个步骤来实现，即步骤一信号先与Chirp信号乘积，步骤二与Chirp信号卷积运算，步骤三与Chirp 信号乘积。将此类方法实现原理理解为1相实现，如图1所示。

这类算法的机理决定了运算前，假设信号在时域和频域上是紧支撑的，然后对时频域进行量纲归一化，时域和频域都被限定在区间［-Δ／2，Δ／2］，宽度为Δ，采样点数为N＝Δ2，采样间隔［11］。而且每个步骤必须考虑采样间隔，以符合香农采样定理。考虑到信号与Chirp信号乘积、卷积运算的Wigner分布区域，需要将支撑区域限定在区间［-Δ，Δ］。为了恢复原来的采样样本值，我们以采样间隔1／2Δ获取样本值，从而得到2N个样本值。并得到离散形式如下：

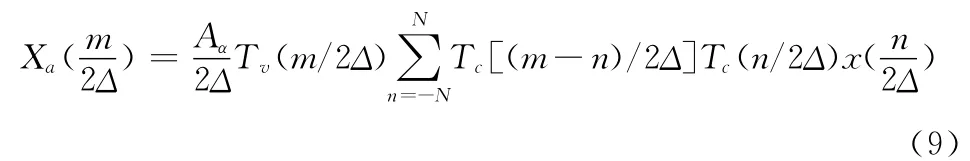
这就是对连续FrFT 的近似值，直接对其计算得到的结果精度低。于是，学者对这类算法进行了改进。目前主要有两种实现途径：一种是由A.M.Kutay实现，另一种是由J.O’Neill实现。前者只允许采样点数N为偶数，且a的取值限定在［-2，2］；后者要求采样点数N为奇数。文献［5］对两者进行了比较，结果显示后者在实际运算中能得到更精确的结果，并对后者进行了改进，消除了限制条件，提出了“最好”的FAFrFT 算法，可实现任意的阶数a和采样点数N的计算。

文献［5］将Ozaktas算法［11］与Pei算法［8］进行了比较，前者是一种实现近似计算连续FrFT 更直接和快速的方法，而后者仅当采样点数N比较大时，才可以用于近似计算连续FrFT。

3.3 二相数值算法

Ozaktas等学者提出的FAFrFT 算法，得到了广泛应用与推广。但是，该算法在计算的时候需要上采样，在计算结束时再下采样，使得计算前后的样本数N一致。从而导致实际计算过程中，有些数据没有必要计算，延长了算法运算时间。为避免此情况，文献［12］提出了一种高效的多相算法，文献［13］提出了一种简化的2相算法。

2相算法在计算过程中，将信号分段成偶数样本和奇数样本部分，分别对这两个部分进行计算，避免没有必要的计算，缩短了算法运算时间。假设信号x（t） 有N个等间隔的样本点数，k的取值可以是整数或者半整数。在计算时，N是偶数或者奇数导致离散样本中的索引值取得整数值或者半整数值。不妨设定将值存放在偶数索引项部分，称之为偶数样本。在这些偶数样本之间定义奇数样本，而这些值是需要通过sinc插值得到的，共有N-1个样本。

偶数样本：

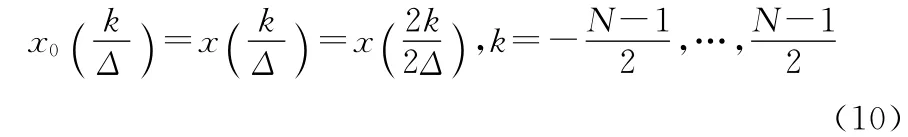
奇数样本：

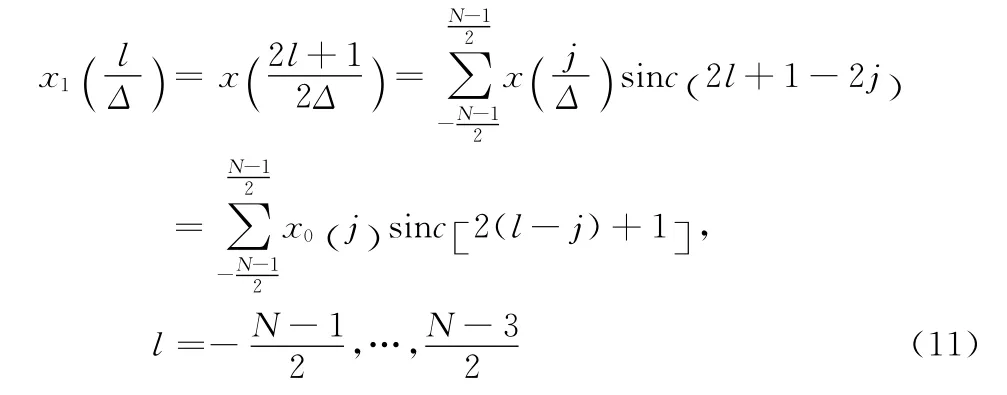
上式含有卷积运算，可以等价于两个FFT 运算乘积的逆FFT 运算（IFFT）。

依照此思路，按照FrFT 的1相实现的三个步骤，可以得 到FrFT 的2相实现［13］，如图2所示。其中As＝Aα／

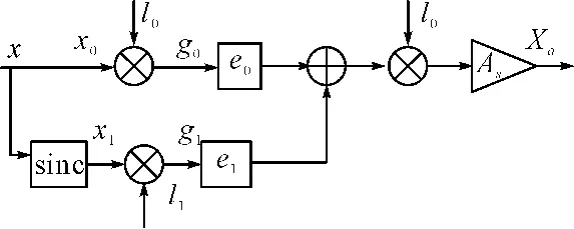
图2 FrFT 的2相实现原理图

4 数值算法性能分析

通过计算机仿真对文献［5］中的算法1与文献［13］算法2进行比较。仿真平台：cpu Pentium（R）Dual-Core 2GHz，cache1MB，系统windows xp sp3，MATLAB R2009a。设定信号为Chirp信号，解析式exp（jπkt2），离散样本个数N＝2n，n＝6，…15，调频率k＝1Hz／s，采样频率fs＝1000Hz／s。FrFT阶数a等间隔从区间［0，2］取100个点。误差系数如图3所示，算法运算时间为Matlab的cputime如图4所示。

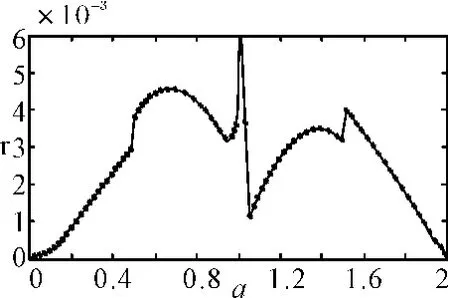
图3 a阶误差系数图

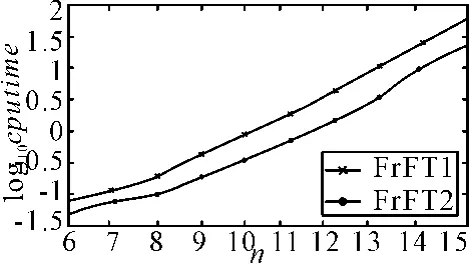
图4 两种算法运算时间图

定义误差系数

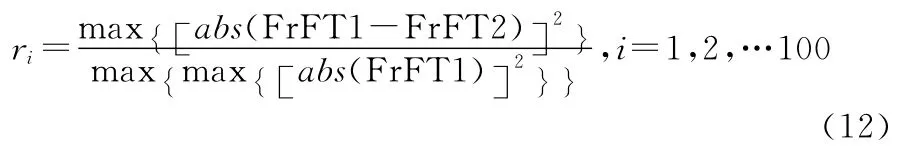
式中abs（·）为取模计算。经计算，rmax＝0.0059。

综合仿真结果可以看出，算法2与算法1的精度相当，而计算速度有较大的提高。

5 结语

FrFT 是对传统FT 的推广，已经广泛应用于雷达、通信、声纳、水印等许多实际工程领域。由于DFrFT 的计算比DFT 的计算要复杂的多，尽管国内外学者提出了很多种FrFT 的快速数值计算方法，但兼顾FrFT 的各种性质和实际计算复杂度，目前还没有一种FrFT 的快速计算方法满足以上所有要求。该文首先给出了分数阶傅里叶变换的整体积分定义、离散分数阶傅里叶变换定义，对现有的主要几种数值算法进行了研究和比较，最后基于Matlab分析了一种二相FrFT 快速算法，经比较其计算速度更快、有更好的实用价值，可以进一步贴近工程领域实时性需求。

［1］Almeida L B.The fractional Fourier transform and time-frequency representations［J］.IEEE Trans on SP，1994，42（11）：3084-3091.

［2］齐林，陶然，周思永，等.基于分数阶fourier变换的多分量LFM信号的检测和参数估计［J］.中国科学，2003，33（8）：749-759.

［3］邓兵，陶然，齐林，等.分数阶Fourier变换与时频滤波［J］.系统工程与电子技术，2004，26（10）：1357-1359.

［4］谢德光，张贤达.基于分数阶Fourier变换的雷达目标识别［J］.清华大学学报，2010，50（4）：485-488.

［5］Bultheel A and Sulbaran H E M.Computation of the Fractional Fourier Trasform［J］.Appl.Comput.Harmonic Anal，2004，16（3）：182-202.

［6］陶然，邓兵，王越.分数阶Fourier变换在信号处理领域的研究进展［J］.中国科学，2006，36（2）：113-116.

［7］Candan C.The discrete Fractional Fourier Transform［D］.MS Thesis，Bilkent University，Ankara，1998.

［8］Pei S C，Yeh M H，Tseng C C.Digital fractional Fourier transform based on orthogonal projections［J］.IEEE Trans on SP，1999，47（5）：1335-1348.

［9］Santhanam B，McClellan J H.The discrEte rotational Fourier transform［J］.IEEE Trans on SP，1996，44（4）：994-998.

［10］Yeh M H，Pei S C.A method for the discrete fractional Fourier transform computation［J］.IEEE Trans on SP，2003，51（3）：889-891.

［11］Ozaktas H M，Ankan Orhan.Digital Computation of the Fractional Fourier Transform［J］.IEEE Trans on SP，1996，44（9）：2141-2150.

［12］TaoR，Liang G，Zhao X H.An Efficient FPGA-based Implementation of Fractional Fourier Transform Algorithm［J］.Sign Process Syst，2010，60（1）：47-58.

［13］Bultheel Adhermar.A two-phase implementation of the fractional Fourier transform［R］.Report TW 588，Dept.Computer Science，K.U.Leuven，March，2011.

［14］张明，柳超，张志刚.鞭天线线性阵列方向图的数值计算［J］.计算机与数字工程，2009（7）.