变精度粗糙集模型在空袭兵器类型识别中的应用＊

（解放军陆军军官学院数学教研室 合肥 230031）

1 引言

在现代防空作战中，空袭兵器的种类多种多样，侦测数据类型复杂，这造成了空袭兵器类型识别困难。但是对空袭兵器类型进行准确、可靠的识别非常重要，它是防空作战决策的重要依据，也是发挥防空武器效能的前提保证。对于空袭兵器类型识别问题，学者们提出了经典粗糙集模型［1］、神经网络模型［2］等多种模型。

粗糙集理论［3］，是由波兰学者Z.Pawlak于1982年提出的一种处理不精确和不确定问题的数学方法，可以对数据进行分析和推理，从中发现隐含的知识。利用经典粗糙集模型解决空袭兵器类型识别问题时需要对连续属性进行离散化，会造成一定程度的信息损失［4］。同时经典粗糙集模型无法处理含有噪声的数据。针对以上问题，该文建立了基于改进相似度的变精度粗糙集模型［5］，提出了基于重要度的属性约简算法并通过一组测试样本对模型进行了检验。

2 空袭兵器的主要类型和识别因素［6～7］

空袭兵器一般分为五种类型：战术弹道导弹、重型兵器（包括轰炸机、歼击轰炸机和歼击机等）、轻型兵器（包括空地导弹、反辐射导弹和巡航导弹等）、武装直升机和诱饵，这五种类型分称为第1类至第5类。

空袭兵器类型识别的主要因素：飞行高度（H）、发现距离（R）、飞行速度（V）、航线特征（Y）和电磁辐射（E）。其中飞行高度（H）、发现距离（R）和飞行速度（V）的值为连续型，航线特征（Y）和电磁辐射（E）的值为离散型。

航线特征（Y）：等高平直飞行、爬升或俯冲、下滑、分岔；

电磁辐射（E）：有辐射和无辐射。

表1中是10个样本及相关数据，其中H、R、V等三个因素的数据是连续型的，Y、E等两个因素的数据是离散型的。

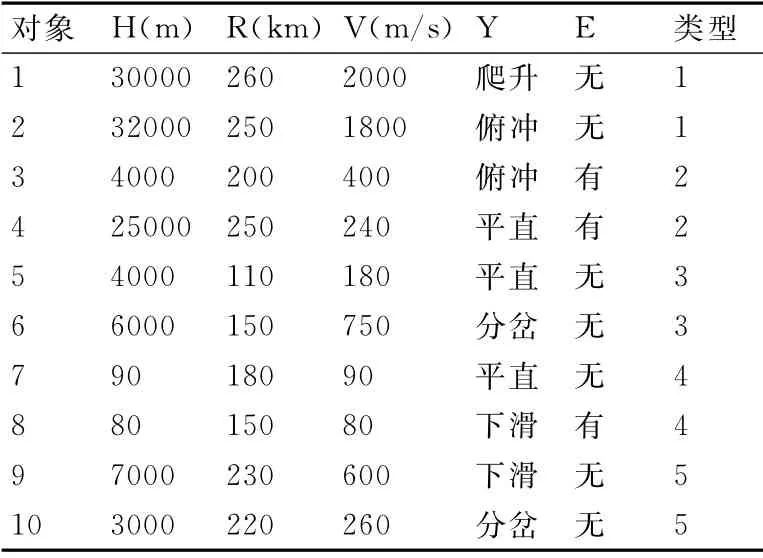
表1 空袭兵器相关数据

3 基于改进相似度的变精度粗糙集模型

定义1［8］设信息系统S＝（U，A，V，f），其中论域U＝｛x1，x2，…，xn｝是非空对象集合；A＝C∪d是非空属性集合，其中C为条件属性集，d为决策属性。

定义2设连续值属性a∈B，对象x，y∈U，则定义x，y关于属性a的改进相似度为

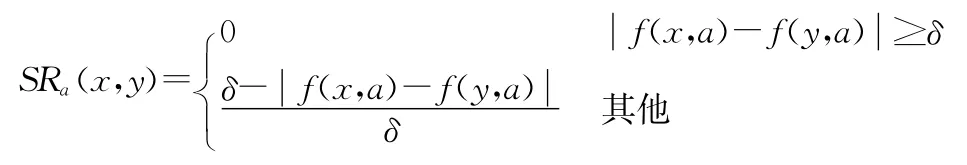
SRa（x，y）∈［0，1］，满足自反性和对称性

如果属性a对应的属性值是离散型，此时，令μ＝，则可得到δ＝1。

定义3设对象x，y∈U，属性集合B⊆A，则对于∀a∈B，x，y关于属性集B的相似度定义为

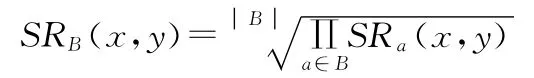
对于∀x，y∈U，计算所有SRB（x，y）构成相似度矩阵HB。

定义4设阈值t∈［0，1］，SRB（x，y）≥t记作xSRtBy。

x关于属性集B的相似类定义为

在不造成误解的前提下，x关于属性集B的相似类SRtB（x）记为SRt（x），相似关系记为SRt。

定义5设（U，SRt）为近似空间，对于对象集合X⊆U，定义X基于相似关系SRt的β下近似集为：

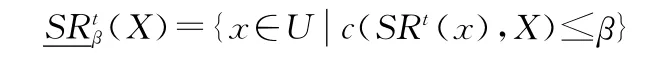
（X）也称为X基于SRt的β正域，记为（X）。

定义X基于SRt的β上近似集：

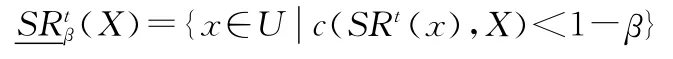
定义6［9］设U／d表示d的等价类集合，则有：

条件属性集B相对于决策属性d的β正域（B，d）定义为

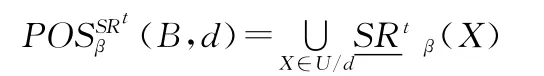
决策属性d与条件属性集B的β近似依赖度γ（B，d，β）定义为

定义7［12］设B⊆C，定义属性c∈C相对于属性集B的重要度SⅠGB（c）为

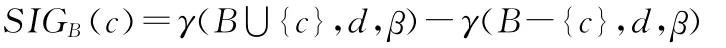
SⅠGB（c）越大，说明在条件属性集B中属性c相对于决策属性d越重要。

定理1［12］在条件属性集C中所有重要度不为0的属性构成C的核CORE（C）。

基于重要度的属性约简算法步骤如下：

1）计算核CORE（C）：对于∀c∈C，计算重要度SⅠGC（c），所有重要度大于0的属性构成核CORE（C）；

2）令RED（C）←CORE（C）；

3）计算γ（C，d，β）及γ（RED（C），d，β）并判断γ（C，d，β）＝γ（RED（C），d，β）是否成立。若成立，则转（6），否则转4）；

4）对所有c∈C-RED（C）计算SⅠGRED（C）（c）并计算其中最大值，即

5）令RED（C）←CORE（C）∪｛cmax｝，转3）；

6）输出最小约简RED（C）。

4 空袭兵器类型识别模型

空袭兵器类型识别的具体流程如图1所示。

图1 空袭兵器类型识别流程图

4.1 数据预处理

表2是由空袭兵器相关数据构成的决策表，论域U＝｛x1，x2，…，x10｝，论域中的每个对象表示一个空袭兵器；条件属性集C＝｛a1，a2，a3，a4，a5｝，a1，a2，a3，a4，a5分别表示H，R，V，Y，E，其中a1，a2，a3为连续值属性，a4，a5为离散值属性，航线特征（Y）的等高平直飞行、爬升或俯冲、下滑、分岔等四种情况分别赋值为1、2、3、4，电磁辐射（E）的有辐射和无辐射等两种情况分别赋值为0、1；空袭兵器的类型为决策属性，则D＝｛d｝，战术弹道导弹、重型兵器（包括轰炸机、歼击轰炸机和歼击机等）、轻型兵器（包括空地导弹、反辐射导弹和巡航导弹等）、武装直升机、诱饵分别赋值为1、2、3、4、5。

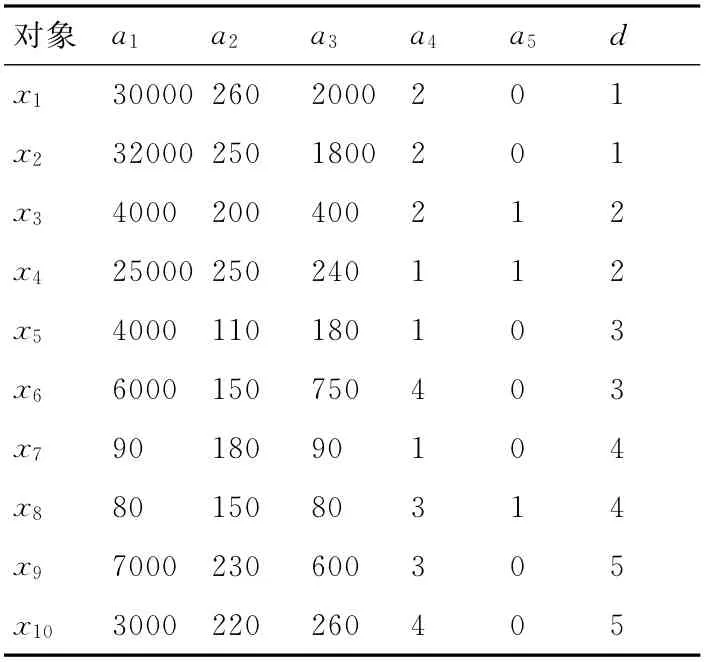
表2 决策表

4.2 计算相似度

利用改进相似关系计算对象关于属性及属性集的相似度，其中，属性a1，a2，a3为连续值属性，设置δ＝2／3；属性a4，a5为离散值属性，设置δ＝1。经计算，可以得到26个相似度矩阵。

4.3 属性约简

本节利用基于重要度的属性约简算法进行属性约简。

决策属性d的等价类集合为

设t＝0.80，β＝0.65，则有：

条件属性集B相对于决策属性d的β正域为

β近似依赖度为

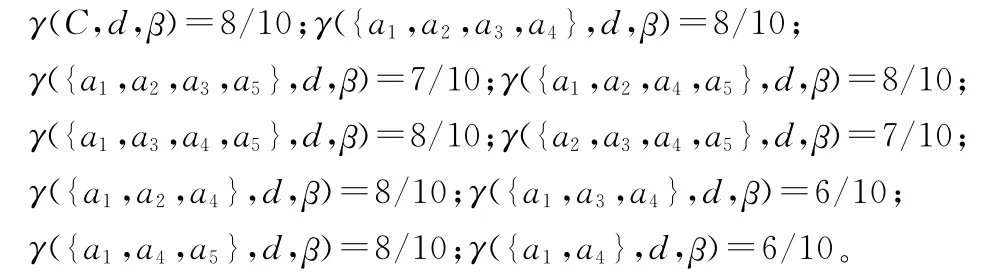
属性重要度为

属性a1和a4的重要度不为0，因此属性a1和a4构成C的核CORE（C），即CORE（C）＝｛a1，a4｝，又知γ（C，d，β）≠γ（｛a1，a4｝，d，β），所以核｛a1，a4｝不是约简。因为γ（C，d，β）＝γ（｛a1，a2，a4｝，d，β）＝8／10，所以｛a1，a2，a4｝是属性集C的约简。

5 数据验证

下面通过表3中的5个测试样本来验证约简结果是否正确，具体方法是：首先剔除测试样本中的非约简属性；然后计算测试样本与表2中样本的相似度；最后验证约简结果是否正确。

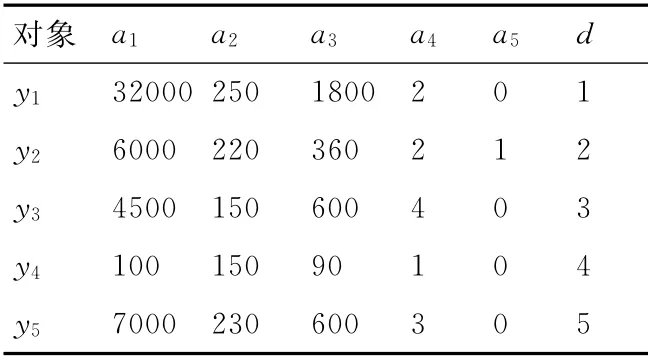
表3 测试样本

剔除测试样本中的非约简属性a3和a5，见表4。

表4 约间后决策表

计算测试样本与表2中样本的相似度，见表5。

y1与x1、x2的相似度分别为0.88、0.79而与其他对象的相似度均为0，已知x1和x2都是第一类，所以判断y1为第一类；同理，可以判断y2为第二类，y3为第三类，y4为第四类，y5为第五类。模型计算得到的结果与测试样本的结果完全一致，说明模型是准确、可靠的。

表5 相似度表

6 结语

该文建立了基于改进相似度的变精度粗糙集模型并提出了基于重要度的属性约简算法。模型克服了经典粗糙集模型的不足，通过对连续值属性直接进行处理，避免了离散化带来的信息损失，同时变精度粗糙集模型允许一定程度上的错误分类，具有了一定的噪声数据处理能力。最后利用一组测试样本对模型进行了检验，结果表明模型是准确、可靠的。

［1］赵双杰，刘进忙.基于粗集神经网络模型的目标识别方法研究［J］.战术导弹技术，2006（4）：47-50.

［2］陈绍顺.基于模糊神经网络的空袭兵器类型识别模型［J］.制导与引信，2004，25（2）：54-56.

［3］Pawlak Z.Rough set［J］.International Journal of Computer and Information Sciences，l982，11（5）：341-356.

［4］王国胤.Rough集理论与知识获取［M］.西安：西安交通大学出版社，2001.

［5］Ziarko W.Variable precision rough set model［J］.Journal of Computer and System Science，1993，46（1）：39-59.

［6］孔媛媛.基于优势关系粗糙集的空袭兵器判别［J］.现代电子技术，2009（22）：29-31.

［7］原晓波，王昆，顾建伟.空袭兵器威胁程度综合判断［J］.舰船电子工，2011，31（7）：35-37.

［8］张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京：科学出版社，2001.

［9］米据生，吴伟志，张文修.基于变精度粗糙集理论的知识约简方法［J］.系统工程理论与实践，2004，24（1）：77-82.

［10］徐贤清，马良荔，时扬.基于距离的粗糙集属性约减改进算法研究［J］.计算机与数字工程，2010（11）.

［11］纪赖恩，李秀娟，许晓东，等.一种改进的基于差别矩阵属性约简算法及其应用［J］.计算机与数字工程，2010（6）.

［12］文志信，金栋，单洁.基于条件嫡约简和粗糙集规则匹配的反辐射无人机作战目标威胁识别［J］.舰船电子工程，2011，31（6）：68-72.