多扇图中保Wiener指数的树

王力工 樊稳茹，张 政,2

(1.西北工业大学应用数学系，中国 西安 710072；2.西安航空技术高等专科学校基础部，中国 西安 710077)

设G是一个连通的简单图，用V(G),E(G)分别表示图的顶点集和边集．图G的顶点数即阶数用n(G)表示．用d(v)表示图G的一个顶点v的度数.如果图G的一个顶点v的度数d(v)=1，则称顶点v为图G的一个悬挂点．图G的一个顶点v的距离是指图G的顶点v到其他所有顶点的距离之和，用dG(v)表示．用G1∪G2表示两个不相交的图G1和G2的并图．联图G1∨G2是指从并图G1∪G2中连接图G1的每个顶点和G2的每个顶点所得到的图．n个顶点的路、圈和星图分别用Pn,Cn和Sn表示．称联图P1∨Pn为n+1阶的扇形图，记为Fn．称联图P1∨(Pn1∪Pn2∪…∪Pnm)为n1+n2+…+nm+1阶多扇图，记为Fn1,n2,…,nm(见图1)．设图G是一个连通图，用dG(u,v)表示图G中顶点u和v的距离，即图G中顶点u和v之间的最短路上的边数．图G的Wiener指数就是指图G的任意两点的距离之和，即

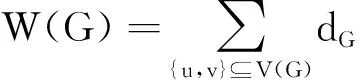
(1)

(1)中的Wiener指数W(G)一般应用在化学中，它是化学图论中最重要的拓扑指数之一．1947年物理化学家Harold Wiener[1]首次研究了无圈分子图的Wiener指数，Hosoya在[2]中把Wiener指数定义为方程(1)的形式．Wiener指数自提出以后，便得到了广泛的研究，一系列的结果相继出现，有关结果参见文献[3～13]．

本文我们考虑文献[4]中提出的一个问题：给定一个连通图G,G中是否存在一棵子树T，使得W(G)=W(T)？很明显要求图G含有圈，并且T不一定是G的生成树．若存在图G中一个子树T，使得W(G)=W(T)，则称T为G的一个保Wiener指数的树．本文给出了多扇图Fn1,n2,…,nm=P1∨(Pn1∪Pn2∪…∪Pnm)中具有无穷多的保Wiener指数的子树，推广了徐幼专、徐立新[9]的结果．

1 相关定义和引理

定义1[7]令树T(n,k)表示一个具有n+k个顶点的似星图,其中一个分支顶点的度为n-1，n-1个顶点的度为1及k个顶点的度为2,且分支顶点到每个1度顶点的距离为1或2,其中k≤n-1，即树T(n,k)是在n阶星图Sn的k条边上各插入一个顶点后所得到的图(见图2)．

图1 n1+n2+…+nm+1阶多扇图Fn1,n2,…,nm 图2 n+k阶树T(n,k)

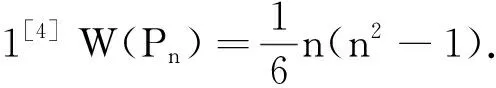
引理2[9]m+1阶扇形图Fm的Wiener指数为：W(Fm)=m2-m+1．

引理3[9]树T(n,k)的Wiener指数为：W(T(n,k))=n2+(3k-2)n+(2k2-5k+1)．

引理4[4]设G1和G2分别是阶为n1和n2的任意两个图，v1∈V(G1)，v2∈V(G2)，图G是将图G1的顶点v1和图G2的顶点v2重叠后得到的图，则图G的Wiener指数为：

W(G)=W(G1)+W(G2)+(n1-1)dG2(v2)+(n2-1)dG1(v1).

2 主要结果

在这一节里，我们给出了多扇图Fn1,n2,…,nm的Wiener指数，并证明了多扇图中具有无穷多个保Wiener指数的子树T(l,k)．

定理1设n1+n2+…+nm=p，则p+1阶多扇图Fn1,n2,…,nm的Wiener指数为：

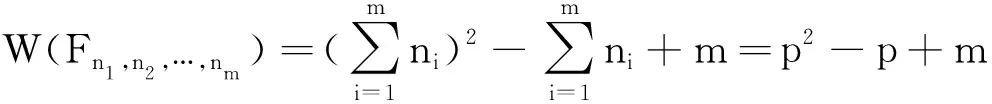
(2)

证对m用数学归纳法，由引理2和引理4即可证明．

定理2设p=n1+n2+…+nm.当下面两个条件中的一个成立时，多扇图Fn1,n2,…,nm有保Wiener指数的子树T(l,k)，这里k≤l-1,l+k≤p+1．

(2)p=(t2+5t+m-b2+b+2)/(2b)，l=(t2+5t+m+b2-b-6bt+2)/(2b),k=2t+1，其中b和m均为正整数，t是非负整数，且b|(t2+5t+m+2)．

证假设W(Fn1,n2,…,nk+1)=W(T(l,k))，且知n1+n2+…+nm=p，由引理3和定理1可得：

p2-p+m=l2+(3k-2)l+(2k2-5k+1)．

上式两边乘4，配方得：

(2l+3k-2)2-(2p-1)2=k2+8k+4m-1．

令x=2l+3k-2，y=2p-1，则有

x2-y2=k2+8k+4m-1．

由不定方程知识可知，上述不定方程有解当且仅当k2+8k+4m-1为奇数或者4的倍数．因此我们讨论下面两种情况：

基于上述分析，可明确实现地理信息生成与地图制图一体化概念模型的步骤：（1）强化制图数据内部的数据质量，面向制图与空间数据建立起共同的数据标准；（2）数据生产平台的建立应以符号化为基础；（3）数据管理与生产流程均需与生产目标相适应。

(1)当k=2t为偶数时，

(x+y)(x-y)=4t2+16t+4m-1．

因x+y和x-y均为奇数，令x-y=2a-1，这里a为正整数，当(4t2+16t+4m-1)/(2a-1)是奇数时，可取

解得：

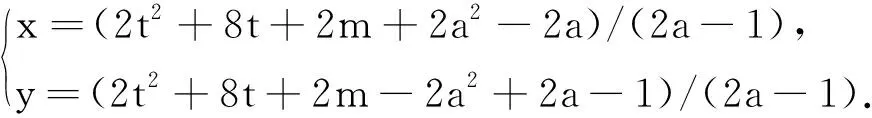
当(4t2+16t+4m-1)/(2a-1)是奇数时，则

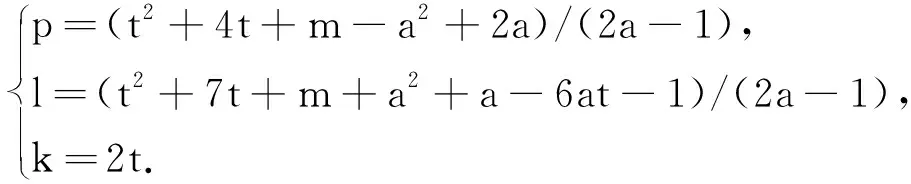
多扇图Fn1,n2,…,nm有保Wiener指数的子树T(l,k)，这里p=n1+n2+…+nm，且对任意的正整数t，均有2t=k≤l-1,l+k≤p+1．

(2)当k=2t+1为奇数时，x+y和x-y均为偶数，则

(x+y)(x-y)=4t2+20t+4m+8．

令x-y=2b，这里b为正整数，当b|(t2+5t+m+2)时，可取：

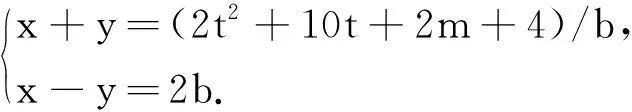
解得：

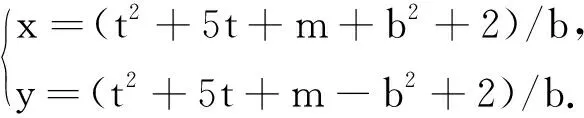
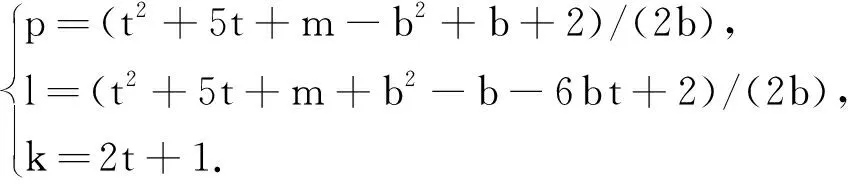
故多扇图Fn1,n2,…,nm有保Wiener指数的子树T(l,k)，这里p=n1+n2+…+nm，其中b和m均为正整数，t是非负整数，显然对任意的非负整数t，均有2t+1=k≤l-1,l+k≤p+1．

推论1设p=n1+n2+…+nm，当下面3个条件中的一个成立时，多扇图Fn1,n2,…,nm有保Wiener指数的子树T(l,k)，这里均有k≤l-1,l+k≤p+1．

(1)p=t2+4t+m,l=t2+t+m+1,k=2t，其中m和t均为正整数．

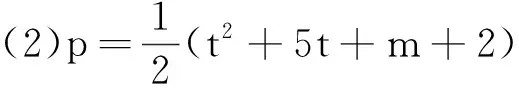
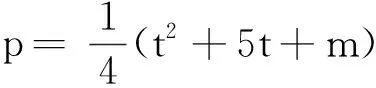
证由定理2，分别取a=1,b=1和b=2，即可证得此推论的(1)、(2)和(3)．

推论2[9]当p=t2+4t+1,l=t2+t+2,k=2t时，其中t为任意一个正整数，扇形图Fp有保Wiener指数的子树T(l,k)，这里k≤l-1,l+k≤p+1．

注记1从定理2可知，在多扇图Fn1,n2,…,nm中存在无穷多的保Wiener指数的子树T(l,k)．

参考文献：

[1] WIENER H. Structural determination of paraffin boiling points[J]. J Am Chem Soc, 1947，69(1)： 17-20.

[2] HOSOYA H. Topological index, a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons[J]. Bull Chem Soc Jpn, 1971,44(9): 2332-2339.

[3] DOBRYNIN A. Branchings in trees and calculation of the Wiener index of a tree[J]. MATCH Commun Math Comput Chem, 2000, 41: 119-134.

[4] DOBRYNIN A, ENTRINGER R, GUTMAN I. Wiener index of trees: theory and applications[J]. Acta Appl Math, 2001，66(3): 211-249.

[5] DOBRYNIN A, GUTMAN I, KLAVŽAR S，etal. Wiener index of hexagonal systems[J]. Acta Appl Math, 2002，72(3): 247-294.

[7] 邓汉元,王红专. 轮形图中保Wiener 指数的树[J]. 湖南师范大学自然科学学报, 2005, 28(4): 1-4.

[8] 刑抱花，潘向峰.某类联图中保Wiener指数的树[J]. 安庆师范学院学报：自然科学版，2008, 14(1): 3-5.

[9] 徐幼专，徐立新. 扇形图P1∨Pm中保Wiener指数的树[J]. 郑州大学学报：理学版， 2006, 38(3): 32-34.

[10] 陈升平.由C6覆盖的环状纤维管的Wiener指数[J].湖南师范大学自然科学学报，2006， 29(3):32-35.

[11] 邓汉元.一类化学图及其线图的Wiener指数(英文稿)[J].湖南师范大学自然科学学报，2009， 32(3):23-26.

[12] 高 云，王力工.两类联图中保Wiener指数的树[J].纺织高校基础科学学报，2010, 23(4):468-472.

[13] 杨 光,刘淑芳.联图Pm∨P2k-1中保Wiener指数的树[J].河北北方学院学报：自然科学版，2010， 26(4):1-3,7.