概率计算中易混淆问题的教法研究

刘建慧

（北京农学院基础部数学教研室，北京 102206）

概率计算中易混淆问题的教法研究

刘建慧

（北京农学院基础部数学教研室，北京 102206）

首先从具体实例提出了物品检验概率计算中一类易混淆问题.然后从理论上证明了无放回逐次抽取中两种概率计算方法的合理性，其定理证明过程充分揭示了这类检验方法与其它相关抽取方式之间的关系并强调了最根本的分析问题思路.最后，研究了文中所得到的一般性结论的适用范围，从而使得这类易混淆问题的讲解变得清晰条理.

随机事件；概率；样本点

1 引 言

从一组物品中随机抽取一部分，计算满足各种检验条件的随机事件的概率是非常具有实用背景的问题，广泛应用于产品抽样检验、彩票中奖率估计等实际问题中.但是，在具体计算概率时，由于涉及对各种事件所包含的样本点的计数，而这些计数问题往往没有一个固定的解题模式可遵循，需要敏锐的洞察力、丰富的想象力和必要的技巧，所以如何引导学生对解决问题的思想方法进行探索、对易混淆的事件进行对比分析是每位任课教师所面临的难点之一.本文就是针对这个问题展开的.

在此类问题中，一般都假设每件物品都是互不相同的或者都是有标识的，这是符合绝大多数产品的生产实际的，原因是：其一，在检验之前，不可能有某件产品与其它产品是否相同的结论产生；其二，对于大件产品，肯定有相应的产品标识，例如工业制造业中的较大部件；而对于没有标识的产品，个体之间在特征形状方面仍然是有差异的，如水果产品中的水果个体就因其在形状、色泽等方面的不同而构成区别于其它个体的自身的特异性.至于彩票，显然都有唯一的标识.因此，在如下的分析中，我们总是默认这种假定.

2 问题的提出

在这类随机实验中，按照抽取物品的方式的不同，实验可以被分为三种类型：1.一次性随机抽取多件.2.每次随机抽取一件，检验之后将这件物品放回原物品群体；下次再随机抽取一件，再放回；依此类推.3.每次随机抽取一件物品，检验之后不将这件放回；下次再随机抽取一件，不放回；依此类推.

对于一次性抽取多件物品的问题，由于不涉及与特定次数相关的事件，所以主要是抽出的物品中满足条件的物品个数的概率问题，适合用组合数的方法求解，理解上不会带来任何问题.但对于后面两种多次抽取问题，由于随机事件可以和具体次数相关，也可以和总的多次抽取的信息相关，所以事件种类比较多，学生极易混淆.对此，不同的教材在处理方面有不同的侧重点，如教材［1］就仅仅对一次性抽取多件物品的问题进行了介绍，而忽略了后两种易混淆问题，这固然缩短了这部分的篇幅，但也使学生课后接触到后两种问题时常感到困惑；为弥补教材［1］的缺憾，教材［2］对三种问题都引入了具体实例，并且为了帮助同学拓展思路，在问题求解时，给出了不止一种方法，如下面的例子.

例1［2］一批产品共80件，其中有10件次品.现不放回地抽取两件，求“取得一件正品一件次品”的概率.

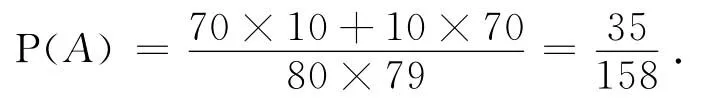
解法二 由于是不放回抽取，所以也可看作不分先后次序一次抽两件.从80件中抽取2件共有C种取法，抽到一件正品一件次品有C·C种，所以

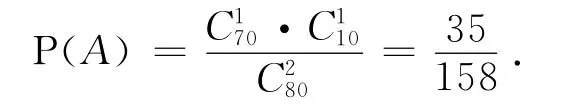
解法一和解法二的总样本点数和事件所包含的样本点数都不同，但计算结果一致.这样的结论是否具有一般性？解法二是否在任何无放回的情形下都适用？请看下面两个分别与一维和二维随机变量分布相关的概率计算问题（以下两个例子均为［2］中作业）.

例2［2］一批零件共有12个.其中有9个正品，3个次品.安装机器时，从这批零件中任取一件，且取出的次品不放回，然后再取一个零件，直到取得正品为止.求在取得正品之前已经取出的次品数的概率分布.

为求解例2，用随机变量ξ代表“在取得正品之前已经取出的次品数”，则ξ的可能取值为0，1，2，3.取这四个值中的任何一个时，都涉及一个无放回多次抽样问题.有的学生利用了例1中解法二的启发，也看作不分先后次序一次抽多件，如“ξ＝1”表示取得正品之前已经取出的次品数为1，则理解为一件次品一件正品，由此直接计算如下：

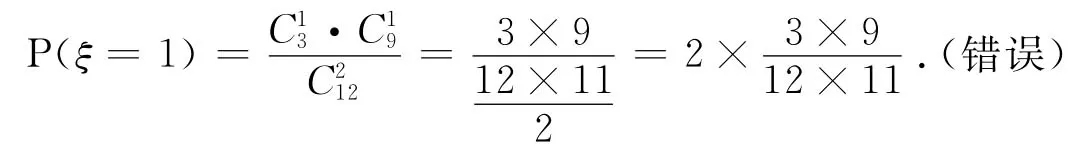
而按照分次的题目原意，总样本点数计算为：第一次抽取的可能数乘以第二次抽取的可能数，也即CC；“ξ＝1”表示第一次为次品第二次为正品：即第一次抽取次品的可能数乘以第二次抽取正品的可能数C，也即，由此得

在这个例子中，按照次序与不分先后次序计算的结果是不同的.

例3［2］一个盒子里有12个小球，其中两个是红球，今从其中随机抽取两次，每次取一球，不放回.若定义两个变量ξ和η如下：

有的学生仍按照例1解法2的思路，得到

这表明，在解决分次无放回抽样概率计算中，需要对不同解法的适用范围进行详尽讨论，还要引导学生掌握最根本的分析方法.因为这种问题不仅仅是局部现象，而是与一维以及多维随机变量分布密切相关.由于教材中都没有涉及这方面的专题分析，所以本文下一节就对一般问题进行讨论，并根据学生在学习中的问题提出便于理解的证明方法，这种证明方法实际上就是这类问题最根本的分析方法.

3 一般性理论及适应范围

定理1 从N件产品（其中D件次品，N-D件正品）中每次取1件产品进行检验，则有

1.在有放回条件下，检验n件产品，恰有k件次品的概率为

2.在无放回条件下，检验n件产品，恰有k件次品的概率为

分析 学生在初次接触这两个式子时感到非常困惑，因为同样都是逐次抽取问题，（1）和（2）式形式上具有很大差异.而（2）式恰好就是一次性抽取的概率公式，似乎与逐次抽取的事实不符.其实，两者都可以从分次的出发点来考虑，下面就给出从分次角度出发的证明.

证有放回和无放回情形都统一用逐次法分析，并用A表示事件“检验n件产品，恰有k件次品”.

1.对于有放回情形，由于每次抽取时产品总数都是N，所以每次选择的可能性均为N，从而抽取n次的样本点总数为Nn.

事件A所包含的样本点数的求解可以按照如下思路进行：

（ii）考虑k件次品在n次中的次序位置固定（同时n-k件正品在n次中的次序位置也就随之固定）时所有可能的抽取数：1）每次抽取到次品的可能性都是D，抽到正品的可能性都是N-D；2）按照乘法原理，n次抽取的可能性数目是各次抽取数的乘积，即k个D和n-k个N-D的乘积，由于乘积是可交换的，所以这个乘积与次品和正品的先后顺序无关.

（iii）综合（1）与（2），就得到在有放回的条件下，事件A所包含的样本点数为C·Dk·（N-D）k.由于样本点总数为Nn，从而得到事件A的概率如（1）式所示.

2.对于无放回情形，由于每次抽取时产品总数都是上一次抽取总数减1：第1次N，第2次N-1，第3次N-2，…，第n次N-（n-1），所以抽取n次的样本点总数为

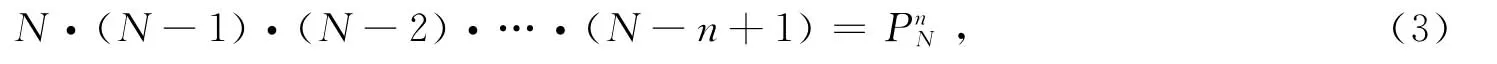
事件A所包含的样本点数按照如下思路进行：

ii）考虑k件次品在n次中的次序位置固定（同时n-k件正品在n次中的次序位置也就随之固定）时所有可能的抽取数：1）每次抽取到次品的可能性都是上一次抽取次品的可能数减1：第1次D，第2次D-1，第3次D-2，…，第k次D-（k-1）；每次抽取到正品的可能性都是上一次抽取正品的可能数减1：第1次N-D，第2次N-D-1，第3次N-D-2，…，第k次N-D-（k-1）；2）按照乘法原理，n次抽取的可能性数目是各次抽取数的乘积，由于乘积是可交换的，所以这个乘积与次品和正品的先后顺序无关.

iii）综合（1）与（2），就得到在有放回的条件下，事件所包含的样本点数为

所以由（6）式可得

也即（2）式得证.由此证明了定理1.

定理1表明，例1解法二的方法是具有一般性的；定理的证明过程表明，（1）和（2）式实际上都来自于类似的逐次分析方法，只是在无放回的情形下可以用数学演算推导出（2）式.所以在给学生讲解（2）式时，可以将上面的证明思路引出，学生的困惑就能够消除.定理的证明过程还解释了例2不可以用（2）式计算的原因，因为例2中的第二次一定是正品，而并非两次中的任何一次，所以这时候就需要回到根本的逐次分析方法，而不可以套用公式（2）.同样的解释适用于例3中P（ξ＝1，η＝0）的情况，而P（ξ＝1，η＝1）的情形是因为两次都是红球恰好符合（2）.综上所述，对于无放回逐次抽取产品问题，只有定理1中所述事件的具体化形式才能用（2）式，也即事件只和正（次）品总数相关，与具体次数的抽取情况无关.否则，就只能用这类问题最基本的逐次分析法进行分析，而不能用一次性抽取多件的方法.

［1］ 张德培，罗蕴玲，等.应用概率统计［M］.北京：高等教育出版社，2000.

［2］ 杜晓林，王玉民，等.概率论与数理统计［M］.北京：气象出版社，2005.

Research on Teaching of the Probability Calculation of Confusable Random Events

LIU Jian-hui
（Department of Basic Sciences，Beijing University of Agriculture，Beijing 102206，China）

The problems in probability calculation of confusable random events are first presented，by the concrete examples.Then a theorem is proposed to generalize two caculation results of one by one no return test.From the proof procedure of the theorem，the relations with other relative tests are demonstrated and the most fundamental analytical method is emphasized.At last，the limitations of the generalized conclusion in the theorem are discussed，which makes the teaching problems clear.

random events；probability；sample points

O211

C

1672-1454（2012）04-0147-04

2008-11-11

北京市属市管高校人才强教计划资助项目（PXM2007-014207-044539）