两种反常积分敛散性的判别方法

龙爱芳

（中南民族大学数学与统计学学院，湖北武汉 430074）

两种反常积分敛散性的判别方法

龙爱芳

（中南民族大学数学与统计学学院，湖北武汉 430074）

介绍了两种判别反常积分敛散性的判别方法.

反常积分；敛散性；判别方法

反常积分是数学分析课程中比较难掌握的内容，在《数学分析》教材（华东师范大学数学系编，第三版）中介绍了比较判别法、比较判别法的极限形式、阿贝尔判别法及狄利克雷判别法；此外文［2］给出了反常积分的对判别法；文［3］介绍了反常积分的导数判别法等等，本文介绍反常积分的另外两种判别法：比值判别法和拉贝判别法.

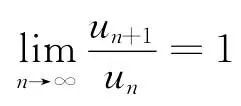
定理1 设f（x）定义于［1，＋∞），f（x）≥0，且在任何有限区间［1，u］上可积，则有

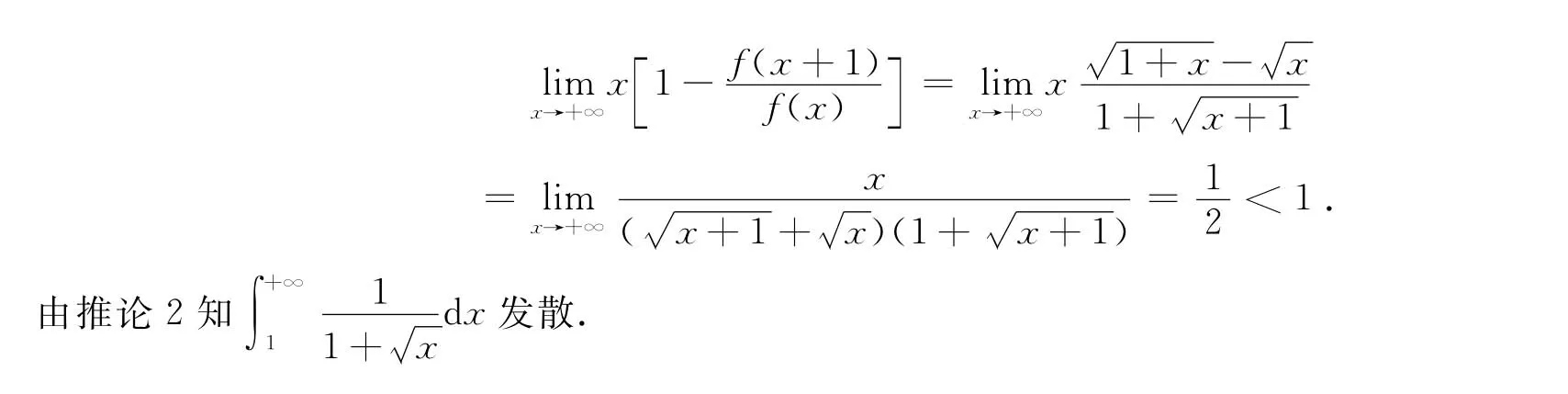
［1］ 华东师范大学数学系.数学分析（上册，第三版）［M］.北京：高等教育出版社，2001：264-280.

［2］ 徐晶.一种反常积分和正项级数收敛的判别法［J］.高等教育研究，2005，8（3）：25-26.

［3］ 郭才顺，黄绍斌.正函数广义积分收敛性的两个判别法［J］.南昌水专学报，2004，23（4）：32-34.

Two Discriminating Methods to Convergence and Divergence of Improper Integral

LONG Ai-fang
（School of Mathematic and Statistics，South-central University for Nationalities，Hubei wuhan 430074）

Two discriminating methods to convergence and Divergence of improper integral are given in this paper.

improper integral；convergence and divergence；discriminating method

O172.2

C

1672-1454（2012）04-0140-04

2010-03-27；

2010-06-24

中南民族大学教研项目（JYX10036）