基于PCA和Eros的多元时间序列聚类分析
2012-11-21郭小芳张绛丽宋晓宁王卫东
郭小芳, 张绛丽, 宋晓宁, 王卫东
(江苏科技大学 计算机科学与工程学院, 江苏 镇江 212003)
基于加权(扩展)欧几里德范数(Extended Euclid Norm,Eros)[1]的主元分析(principal component analysis, PCA)[2]是一种处理高维数据的有效方法.这种方法通过原始数据的适当线性组合,把多元时间序列数据集分解为若干个簇,在每个簇中任选一代表元素,根据簇的代表元素与剩余MTS元素的前若干个主元与之间的Eros范数,将剩余元素划分给最近的一个簇,再用剩余元素替换代表元素,再次进行操作,当各元素所在的簇不再改变为止(或超过限定迭代次数)[3-4].这种方法在计算范数时对原有的复杂数据进行降维,可以给出数据的主要成分和有用信息,去除数据中的噪音和冗余.文中采用一种基于主元的K-近邻的MTS数据聚类算法,根据多元时间序列数据的主元及其范数进行K近邻聚类分析.理论分析和实验结果表明该算法聚类结果质量和运行时间明显优于直接利用k-均值法的聚类结果.
1 PCA原理分析
在以原始变量X1和X2为坐标的平面上(图1),数据点分布在一个倾斜的椭圆内,表明原始变量X1和X2之间相关性很强.如果在平面上作一个坐标变换:
(1)
在Z1Z2坐标下,数据点主要沿着Z1方向的分布,Z2方向上数据的变化不大,在一定条件下可以忽略,从而将原来的二维问题看做一维问题来处理,达到降维的目的[5].主元分析技术[6]通过对原有数据进行适当操作,将原有的复杂数据降维,揭示隐藏在复杂数据背后的简单关系.这种方法首先获得每个矩阵的主元,然后试探性选择z个主元,这前z个主元素之间的相似性通过下式计算:
(2)

图1 主元分析的几何意义
这里要求MTS项A和B具有相同列数,可以有不同的行数.式(2)中,L和M各自包含矩阵A和B的前z个主元,θi j为A的第i个主元与B的第j个主元之间的夹角.即从0到z,通过计算两矩阵的前z个主元两两之间的余弦平方值来测量其相似性.方法简单,无参数限制,可以方便的应用于各种场合.
2 扩展欧几里德范数(Eros)
设A=[a1, …,an],B=[b1, …,bn],ai和bi为单位正交向量,其夹角为θi,则矩阵C=A-B=[a1-b1,…,an-bn,]的F-加权范数的平方可用如下公式计算:
(3)

对于MTS项A和B,其扩展欧几里得范数(Eros) 定义为
(4)
式中:ai和bi为协方差矩阵为MA和MB的右特征向量(列正交向量,长度为n);w为基于MTS数据集特征值的加权向量;θi是ai和bi之间的夹角.Eros从0到1变化,反映了A和B之间的相似程度,1表示最相似.定义A和B之间的Eros距离:
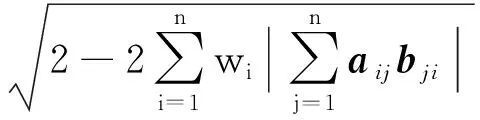
(5)
即利用包含主元及相关特征值的右特征向量矩阵测量两个MTS主成份间距离.
根据式(5),若Eros(A,B,w)>Eros(B,C,w),则有
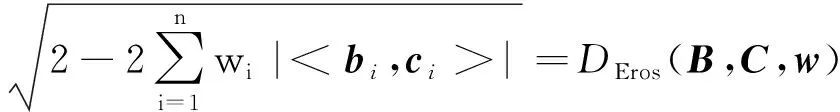
(6)
即DEros(A,B)小于DEros(B,C),可见DEros也保存了Eros的距离.
3 多元时间序列的聚类分析
K-means算法将类的均值作为聚类中心,较好地体现了聚类的统计意义[7-8],是当前普遍应用的聚类方法之一.正是这个原因,也导致其无法用于具有类别属性的数据.
基于主元的聚类分析的思路是:对于n个数据元素的MTS数据集,分为k(k≤n)个目标簇,簇内的元素相似,不同簇元素相异[9].任选某簇内元素作为代表,取簇外剩余元素的前z个主元计算其与代表元组的范数,以此为依据来决定将剩余元素分配给最近一簇,同时用剩余元素替换代表元素,反复操作,当各簇元素不再变化为止[10-11].这种方法的算法描述如下:
输入:MTS数据的主成分序列
输出:k个聚类
流程:
① 选取参考点,取元素(C1,C2,…,Ck)作为初始聚类的中心;
② 对于新序列点a,根据上述范数将其划入与其最近的类,合并后类的半径为r1;
③ 用相同的方法找出原有类中最相近的两类,合并后的类半径为r2;
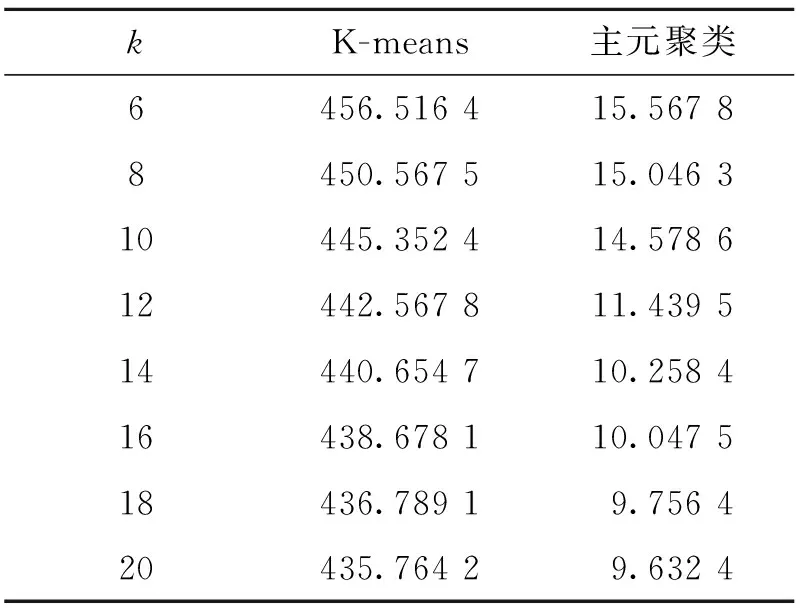
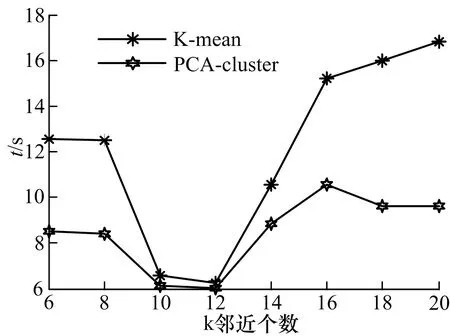
④ 比较r1和r2,若r1 ⑤ 对所有MTS主成分重复步骤②~④,直到整个MTS主成分序列扫描结束; ⑥ 输出k个聚类. 如有m个参考点,则每个数据对象就会有m个距离,p是最佳参考点,查询点为q,查询半径为rq.建立索引结构,当某聚类c与查寻区域相交时,利用前述三角不等式进行过滤,查询聚类c中以p为圆心,内外半径为r1,r2的圆环与聚类c相交的区域中的点.中类被分解为核心聚类环与边缘聚类环,对这些聚类环分别进行索引,可以进一步提高数据过滤效率. 算法: 主元聚类分析算法; 输入: MTS数据集,聚类数k,主元数z; 输出:k个MTS主元序列的聚类中心. ①[A,w]←PCA(MTS); ② C←select(A,k);//选择初始类中心 ③num←0; ④ whilenum ⑤ for eachainA ⑥ for eachcinC ⑦ d←dist(a,c,w,z);//计算到各个类中心点距离 ⑧ end ⑨i←min(d,a);//距离A 最近的类. ⑩end 取某股市300家上市公司的交易数据作为实验数据集,股票长度为300个交易日的观测值,选取开盘、收盘价、最高、最低价、交易量和交易金额等6个变量.利用Matlab7.9a 检验实验算法.虽然MTS项经过PCA处理,但还不是单变量序列,不能用传统的相似性方法进行相似性度量.由于各主成分对整体数据的贡献率不同[12],其方差反映了原变量在主成分上的集中程度,因而将方差作为贡献率权值.设方差贡献率为SYi/∑SYi,各成分对应的权值为ωi=SYi/∑SYi. 实验过程中,主元z的选取也会对算法结果产生一定的影响.当股票样本数为300时,主元数z及其的贡献率见表1.可以看出当z=2时,它们的累积贡献率就高达99%,这说明取前2个主元就可以很好地代表原始数据,所以一般在验证算法时取z=2即可. 表1 主元z的贡献率 为了估算聚类结果的质量,定义聚类算法的聚类质量: (7) 式中:E表示数据集所有元素的平方误差的总和;p代表任意元素;mi表示簇Ci的中心点.E值越小聚类质量越好. 1) 主元聚类分析和K-means的聚类质量比较 为比较主元聚类算法和K-means算法的聚类质量值E,表2给出了k值从6到20变化情况下主元聚类算法与K-means算法的聚类质量.从表中可以看出主元聚类算法在聚类质量上明显优于K-means算法,且随着近邻数k值的增加聚类质量值E值减小的比例更大,聚类效果更好. 表2 两种算法的聚类结果值E比较 2) 主元聚类分析和K-means的执行效率比较 针对上述股票数据集,比较了在不同的近邻数k值条件下,主元聚类算法与K-means算法耗费CPU时间见图2,其中,近邻数k值分别取6~20.可见PCA-cluster的执行效率优于K-means算法,特别是当近邻数k在10~12时算法执行速度最快. 图2 两种算法耗费CPU时间比较 从以上结果容易看出基于主元聚类的多元时间序列聚类算法的聚类质量结果明显优于直接利用K-means法时的聚类结果,运行时间也少于直接利用K-means法的运行时间,而且重复次数越多,运行时间越少.表明基于PCA的MTS聚类方法是一个简单有效的聚类方法. 为提高MTS聚类分析的效率,采用基于主元的聚类分析方法.将多元MTS数据集分为k个簇(k小于数据元组个数n),在每个簇中任选一代表元组,根据代表元组与剩余元组的前z个主元的Eros距离对MTS数据进行聚类.实验结果表明该方法聚类质量和运行时间明显优于直接的K-means方法. [1] Sambasivam S, Theodosopoulos N.Advanced data clustering methods of mining Web documents [J].IssuesinInformingScienceandInformationTechnology, 2006(3):563-579. [2] Yang K, Shahabi C. An efficient k nearest neighbor search for multivariate time series [J].InformationComputation, 2007, 205(1): 65-98. [3] Wang Xiaozhe, Smith K A, Hyndman R J. Dimension reduction for clustering time series using global characteristics[J].LectureNotesinComputerScience, 2005, 3516:792-795. [4] Zhao F, Jiao L C, Liu H Q.Spectral clustering with eigenvector selection based on entropy ranking [J].Neurocomputing, 2010, 73(10/11/12): 1704-1717. [5] Filippone M, Camastra F, Masulli F. A survey of kerne land spectral methods for clustering[J].PatternRecognition, 2008, 41:176-190. [6] 郭小芳, 张绛丽. 基于加权范数的多维时间序列相似性主元分析[J]. 江苏科技大学学报:自然科学版, 2011, 25(5): 466-469. Guo Xiaofang, Zhang Jiangli. Similarity PCA of multivariate time series based on extended Frobemus norm[J].JiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2011,25(5):466-469.(in Chinese) [7] Gelbard R,Goldman O,Spiegler I.Investigating diversity of clustering methods:An empirical comparison [J].Data&KnowledgeEngineering, 2007, 63(1):155-166. [8] Birant D,Kut A.ST-DBSCAN: An algorithm for clustering spatial-temporal data [J].DataKnowledgeEngineering, 2007, 60(1):208-221. [9] Pilevar A H,Sukumar M.GCHL: A grid-clustering algorithm for high-dimensional very large spatial data bases [J].PatternRecognitionLetters,2005,26(7):999-1010. [10] Naseimento M, Carvalho A.Spectral methods for clustering-a survey [J].EuropeanJournalofOperationalResearch, 2011, 211(2):221-231. [11]Zhang Z, Jordan M. multiway spectral clustering: a margin-based perspective [J].StatisticalScience, 2008,23(3):353-403. [12]Climescu-Hauliea A.How to choose the number of clusters: the cramer multiplicity solution[C]∥AdvancesinDataAnalysis.Berlin Heidelberg:Springer,2007:15-22.4 实验及结果分析
4.1 实验数据集
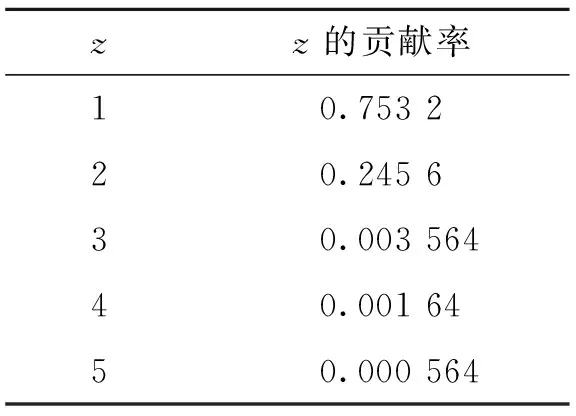
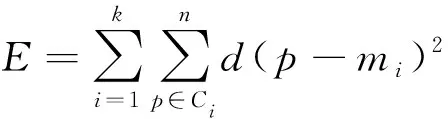
4.2 实验结果
5 结论
