具有时延的遥操作机器人系统稳定性与透明性研究
2012-11-21曾庆军刘海霞赵呈涛
曾庆军, 刘海霞, 赵呈涛
(江苏科技大学 电子信息学院, 江苏 镇江 212003)
遥操作机器人是指在人的操纵下能在远距离,人很难接近或操作有难度的环境中完成比较精细复杂任务的一种远距离操作系统.它拓展了人类的作业空间,在医疗、微生物、微机械等领域都有广泛应用前景[1].然而,基于网络的遥操作机器人系统在实际应用中受到很多不确定因素的影响,诸如网络带宽和网络传输协议的局限性,以及主从机械手及环境建模的误差,其信号传输时延不仅大而且时延大小通常具有随机性,同时还会出现数据丢失、乱序等问题,严重影响了系统的鲁棒稳定性,降低了系统的操作性能.近年来,时延对遥操作机器人系统的影响引起了国内外很多学者的广泛关注[2-3],所采用的控制策略虽然使得系统对时延和参数具有鲁棒稳定性,但时延越大,系统操作性能越差,并不能使透明性达到最佳.而遥操作机器人系统的稳定性和透明性是相互制约的,因此,设计的控制器必须是稳定性和透明性的折衷[4-5].
文中针对遥操作机器人系统中存在的通信时延,将系统描述成一个具有时延的状态方程,通过构造适当的李雅普诺夫函数,分析了时延系统处于约束运动状态下的稳定性,然后给出了系统的等效电路图,采用阻抗匹配的方法分析了系统在有时延和无时延两种情况下的透明性.仿真实验结果表明该方法使时延系统在保证稳定的基础上实现了良好的透明性.
1 遥操作机器人系统模型
遥操作机器人系统主要由操作者、主机械手、网络通信环节、从机械手和作业环境5部分组成(图1).

图1 遥操作机器人系统框图
图1所示系统的动力学模型描述如下[6-7]:

(1)
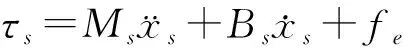
(2)
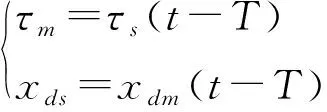
(3)
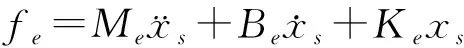
(4)
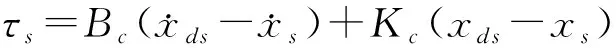
(5)

2 稳定性分析
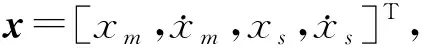

(6)
式(6)可以表示为:
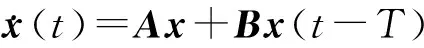
(7)
式中:
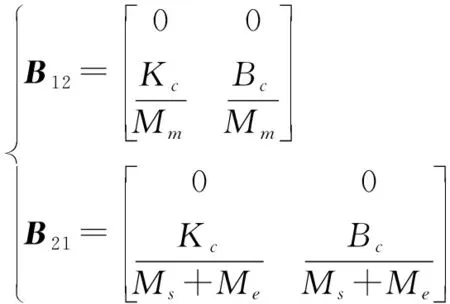
(8)
利用Lyapunov稳定性理论分析式(7)所示系统的稳定性,即通过选取以下Lyapunov函数来分析[8]:
(9)

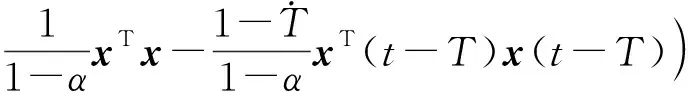
(10)
由于
2xTBx(t-T)≤xTBBTx+xT(t-T)x(t-T)
式(10)可化简为
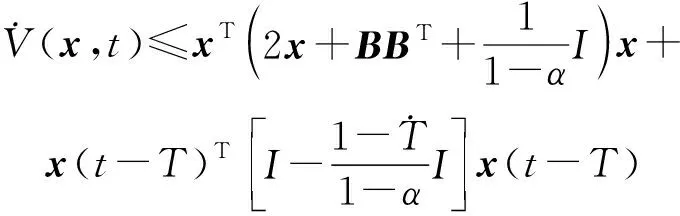
(11)

(12)
满足上式解的条件是矩阵U的特征根应全部具有负实部,即Reλi(U)<0.
由式(12)得
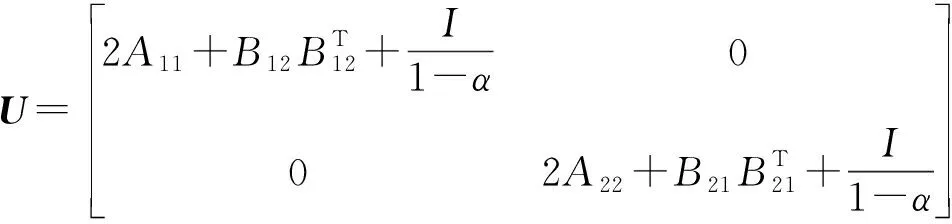
(13)
由上式知U为对角阵,式(13)就可以化简为
(14)
(15)
即:
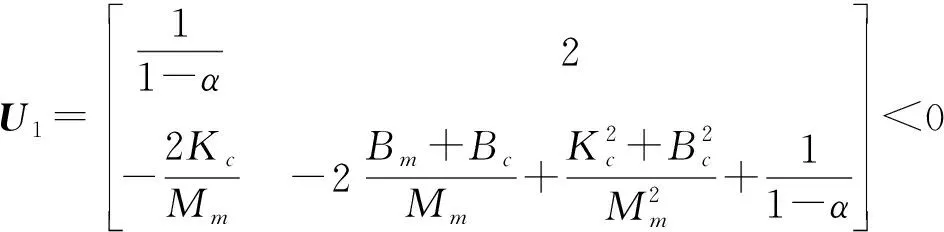
(16)
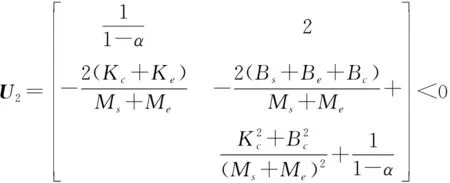
(17)
由U1的特征多项式可以计算出U1的特征根det(U1-sI)=s2+a1s+b1,式中:
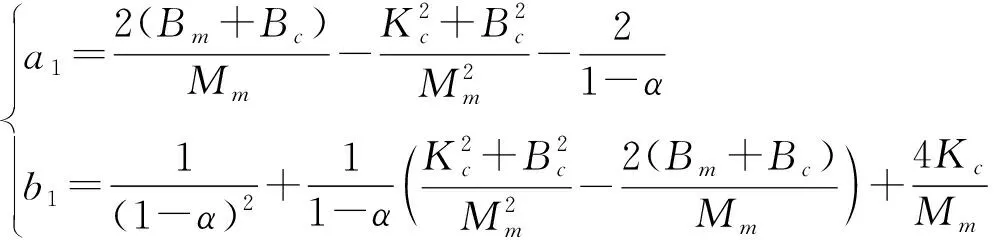
(18)
由此得
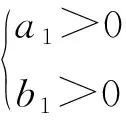
(19)
同样可以计算得到满足式(17)的条件:
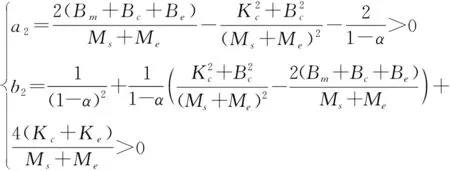
(20)
通过选择适当的Lyapunov函数,得到了遥操作机器人系统的稳定性条件,即:Mm,Ms,Me,Bm,Be,Bc满足式(18),(19),(20).由此可以知道:当Mm,Ms,Bm一定时只要Bc,Kc,Me,Be,Ke满足这3个等式,就能保证系统的稳定性.环境参数Me,Be,Ke为任意值时,就可以得到Bc,Kc的取值范围,从而设计所需的控制器.
3 透明性分析
遥操作机器人系统的两个重要性能指标是稳定性和透明性.当系统透明时,操作者对作业环境的位置和受力具有真实的力觉感受.根据阻抗分析的方法,当作业环境的阻抗和主机械手感觉到的从机械手端的阻抗(又称虚拟阻抗)相等,即Ze(s)=Zv(s)时,具有最佳的临场感效果,此时,操作性能最优,系统完全透明[9].
Ze(s)=Fe(s)/Vs(s)
(21)
Zv(s)=Fm(s)/Vm(s)
(22)
式中:Fe(s),Vs(s),Fm(s),Vm(s)分别为fe(t),vs(t),fm(t),vm(t)的拉普拉斯变换.
假设从机械手始终与作业环境保持刚性接触,则力和位置的双边关系可以用二端口混合矩阵表示:
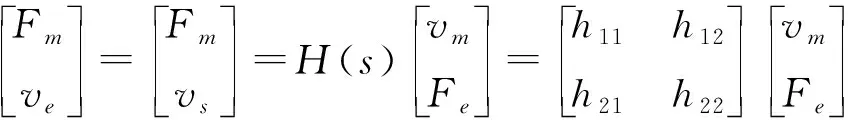
(23)
由式(21,22,23)可以得到虚拟阻抗和作业环境阻抗的关系为:
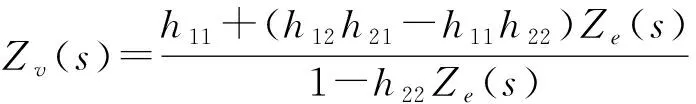
(24)
以下分别分析系统在有时延和无时延两种情况下的透明性.
3.1 无时延情况下系统的透明性
对于实际系统,操作者与作业环境的模型是不确定的,主、从机械手及传输线是固定的,无时延系统可等效为图2所示的电路图[10].
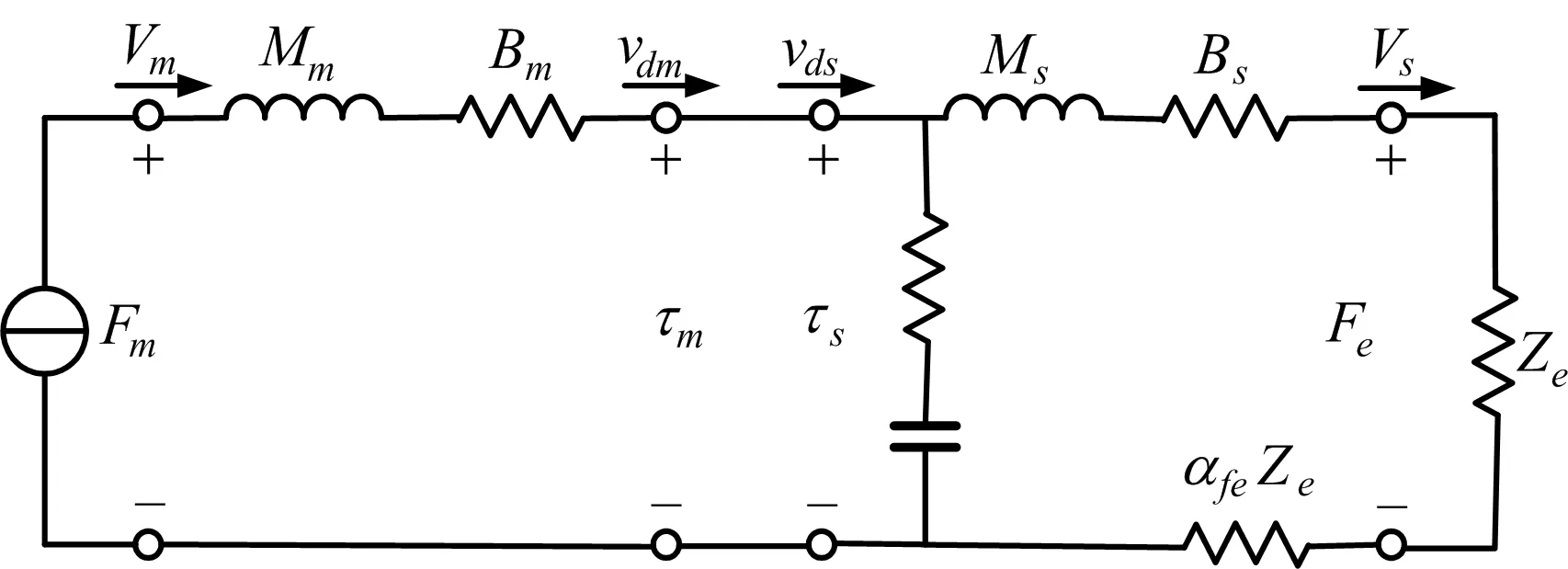
图2 无时延系统的等效电路图
其中从机械手模型表示为:
(25)
通信环节:
(26)
其他部分模型如图1.
由式(25)且vs=Fe/Ze,得
由于环境阻抗比从机械手的阻抗大的多,所以引入参数αf且αf取足够大的值时,有
τs≈(1+αf)fe
(27)
以下将从机械手与环境的接触力分为两种情况进行讨论.
3.1.1 环境与从手的接触力为实际接触力
当作业环境与从机械手之间的力为实际接触力时,由式(1,26,27)得到:
(28)
上式在复频域中可表示为:
Fm=Zmvm+(1+αf)F
(29)
由式(25)得
Bc(vds-vs)-αffe
令Zm=Kc/s+Bc,则
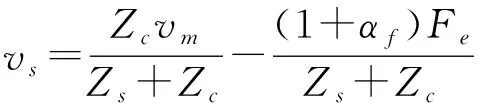
(30)
式(23)结合式(29,30)可得混合参数为:
(31)
则有
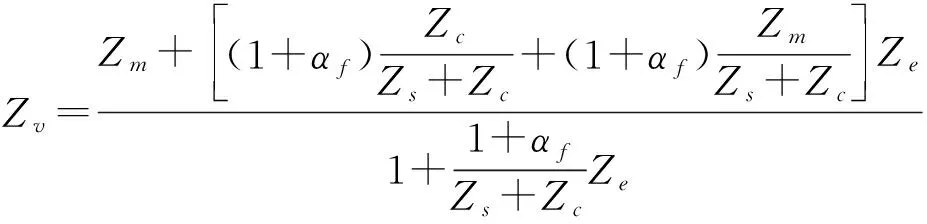
(32)
若Zm→0,Zc≫Zs与实际情况相符,则
(33)
令Zc=kZe(k为从机械手端控制阻抗与环境阻抗的比值)
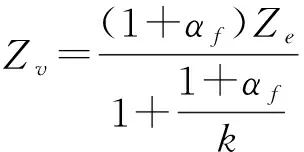
(34)
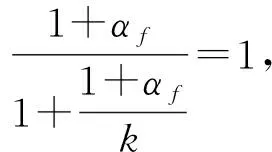
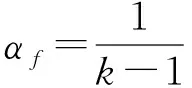
(35)
此时,遥操作机器人系统的透明性达到最佳.由于αf取足够大的值,所以k的取值范围趋向于1,这说明从机械手端阻抗与作业环境阻抗非常接近,特别符合遥操作机器人系统力觉临场感的要求.
3.1.2 环境与从手的接触力为虚拟接触力
当作业环境与从机械手之间的力为用虚拟接触力表示时,由式(1,5)得:
(36)
由式(35,41)得出系统的混合矩阵为:
(37)
故
(38)
代入式(24),同时假定Zm→0,Zc≫Zs,Zc=kZe得
(39)
通过比较式(34)和(39)的结果完全相同.这说明引入虚拟接触力也能使系统达到理想的透明性.
3.2 有时延的情况
遥操作机器人系统的主从端之间存在时延时,其等效电路如图3[9].

图3 具有时延系统的等效电路
图3所示系统的通信环节表示为:
(40)
当k≈1,Zs≪Ze时,从手受到的力:
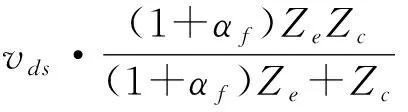
(41)
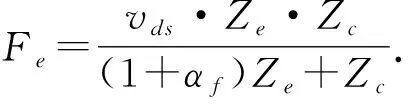
令Zc=kZe,得
(42)
根据Anderson无源控制理论知,为了使系统在任何时延下能够保持稳定,需要对时延的影响进行一定的补偿,可以通过在传输线两端分别加上换算因子n和1/n实现.控制算法变为[9]:
τm=τs(t-T)+n2[vm(t)-vds(t-T)]
(43)
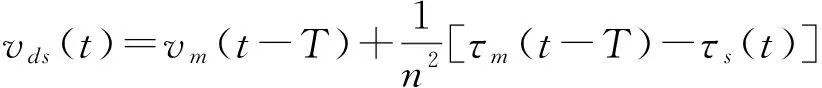
(44)
在自由运动状态下,基本可以实现良好的透明性.下面研究系统在受限运动状态下的透明性.
频域下由式(1,43)得
(45)
由式(25)得从机械手端:
Mssvs=-(1+αf)Fe+(k+1+αf)Fe
(46)
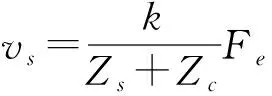
(47)
式(23)结合式(45,47)可得混合参数为
(48)
则当环境阻抗Ze=Mes+Be+Ke/s时,

(49)
虽然虚拟阻抗Zv(s)中没有环境阻抗Ze(s),但是式(49)中n2被看作特征阻抗,体现作业环境的阻抗,所以通过调整n2的值来产生较好的临场感效果,透明性较好.
4 仿真实验结果与分析
为了验证理论分析的结果,使用Matlab 7.0对系统进行仿真,设定参数:换算因子n=0.18,Mm=Ms=1.532 kg,Bm=Bs=0.051 N·s/mm,Me=1 kg,Be=0.12 N·s/mm,Ke=0.1 N/mm,主从手在非自由运动状态下的位置跟踪曲线分别如图4,5;力跟踪曲线分别如图6,7.
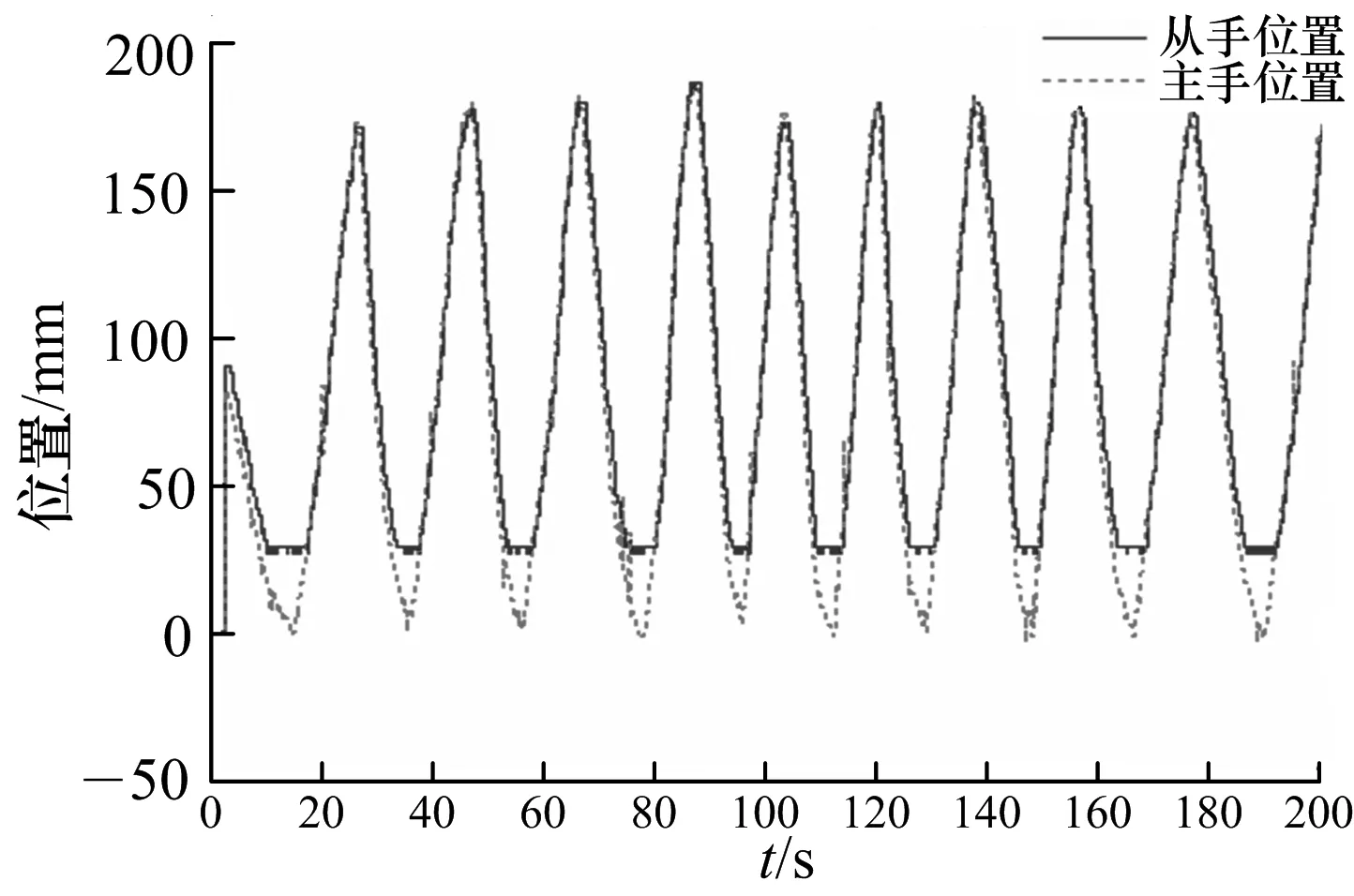
图4 无时延情况下从手对主手的位置跟踪
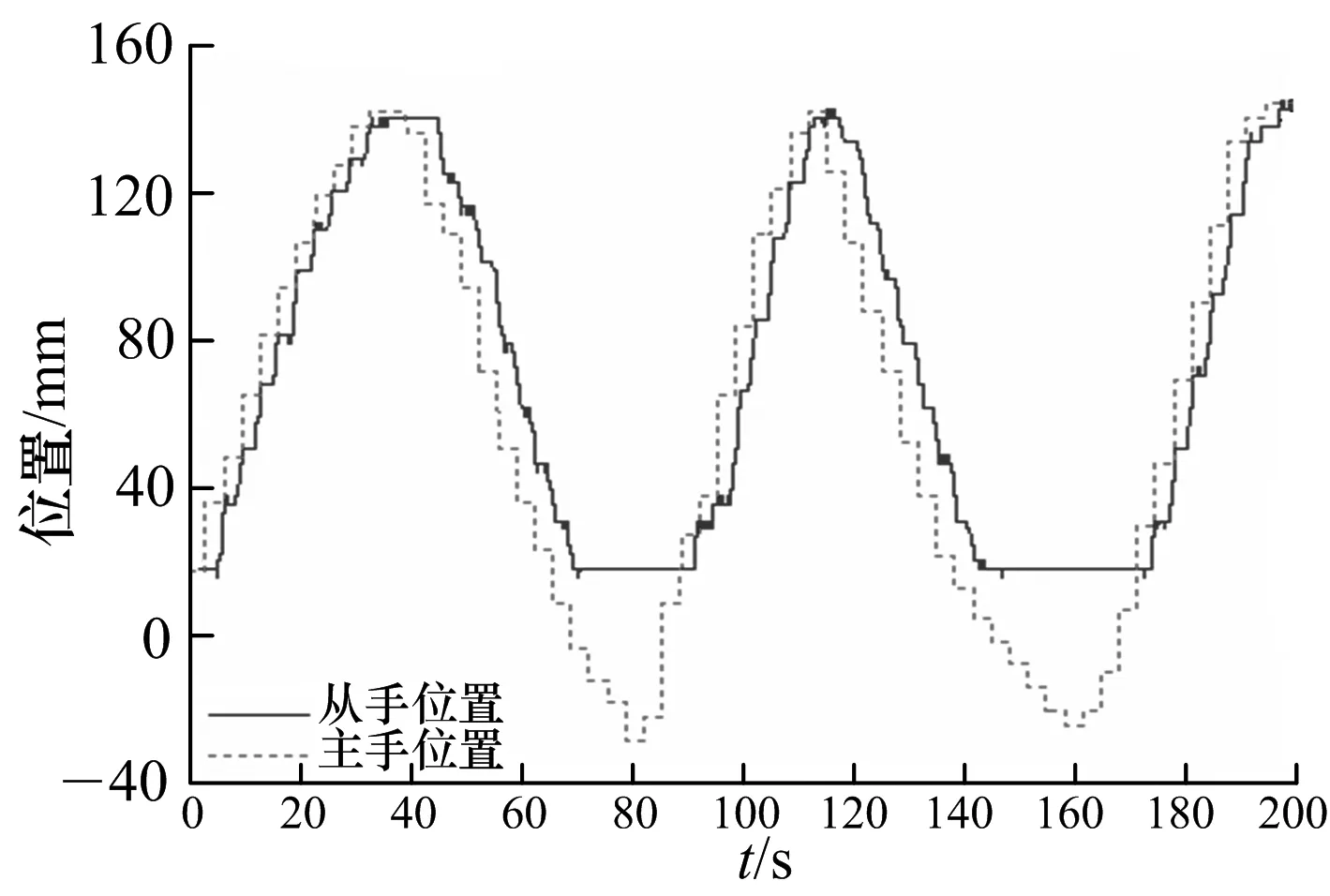
图5 时延(T=4 s)情况下从手对主手的位置跟踪
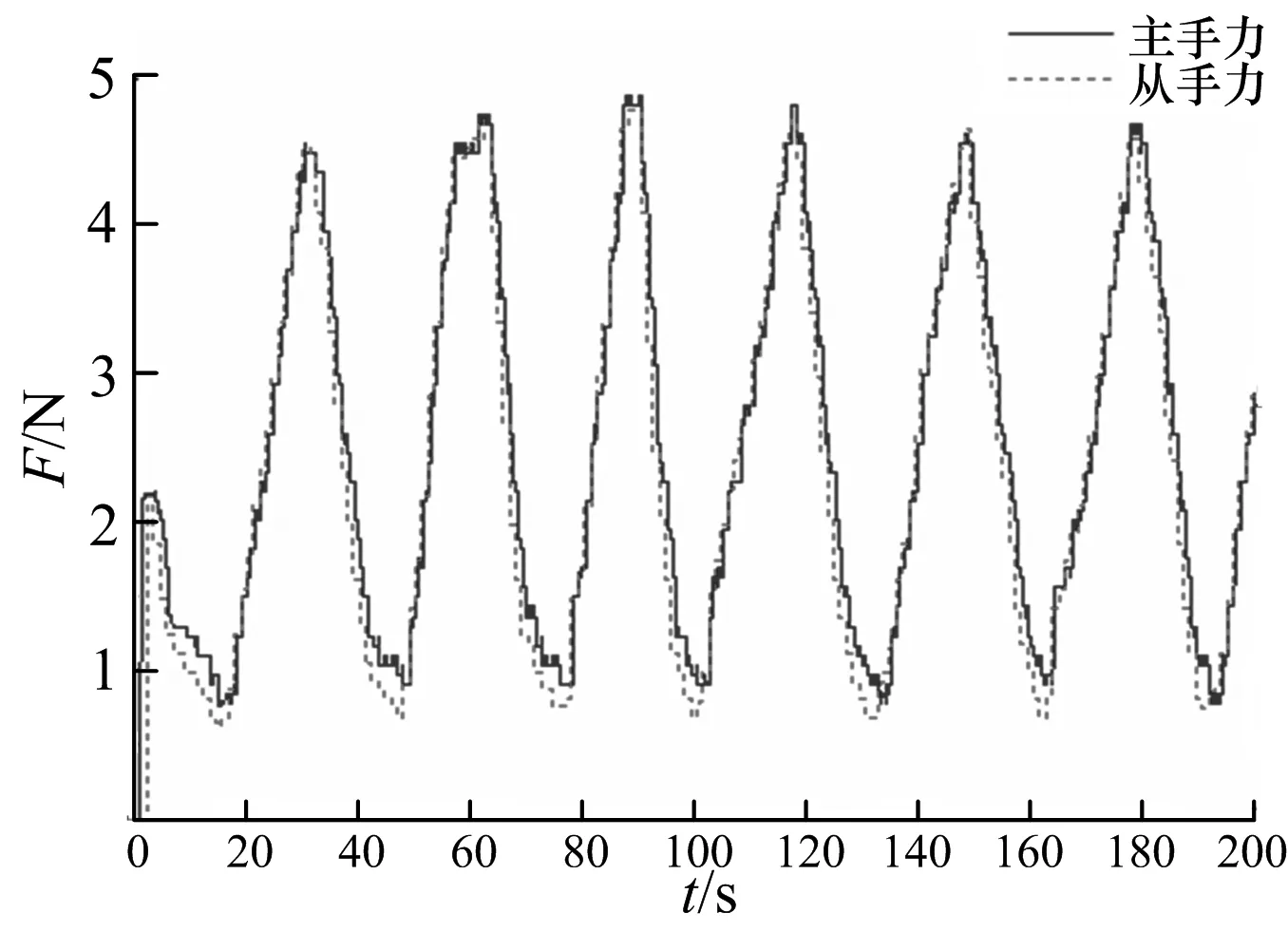
图6 无时延情况下主手对从手的力跟踪
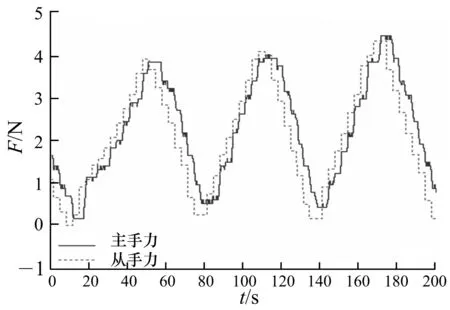
图7 时延(T=4 s)情况下主手对从手的力跟踪
从上图可以观察到无论遥操作机器人系统有无时延,当从机械手未接触环境时,从机械手能够稳定、准确地跟踪主机械手的位置,并且位置误差较小;当从机械手与环境接触时,主机械手根据控制算法继续正转,从机械手不能跟随主机械手运动,符合预料的结果,此时,主机械手给操作者以反馈力,从而使操作者感受到从机械手与环境的作用力,即力觉临场感的实现.图4,6说明无时延情况下系统不仅能够保持稳定,从机械手能够很好跟踪主手的运动,而且主机械手对从机械手有较好的力跟踪效果,操作者具有真实的力觉感受,系统的透明性达到最佳.图5,7说明有时延(时延较大)情况下,系统仍能够保持稳定,具有较好的位置跟踪性能,尽管操作者不能实时感受到从机械手与环境的交互力,但主机械手对从机械手延时后的力跟踪效果较好,系统的透明性较好.
5 结论
1) 针对通信时延对遥操作机器人系统稳定性和操作性能的影响,用Lyapunov函数证明了时延下系统处于约束运动状态下的稳定性;
2) 研究了一种采用阻抗匹配方法分析系统在有时延和无时延情况下的透明性;
3) 实验结果和理论分析表明以上方法在保证系统稳定的基础上实现了良好的透明性.
[1] 杜志江, 孙立宁, 富历新.医疗机器人发展概况综述[J].机器人,2003,25(2):182-187.
Du Zhijiang, Sun Lining, Fu Lixin. An overview of medical robots[J].Robotic, 2003, 25(2):182-187. (in Chi-nese)
[2] 景兴建.网络遥操作机器人系统稳定性分析和规划方法研究[D].中国科学院沈阳自动化研究所,2004:4-20.
[3] Polushin I G, Tayebia A, Marquez H J. Control schemes for stable teleoperation with communication delay based on IOS small gain theorem[J].Automation, 2006, 42: 905-915.
[4] 曾庆军, 王春景.带有柔性关节从机械臂遥操作机器人系统滑模控制研究[J].江苏科技大学学报:自然科学版, 2011, 25(1): 54-59.
Zeng Qingjun, Wang Chunjing. Sliding-mode controller for a teleoperation robot system with elastic-joint slave manipulator[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2011, 25(1): 54-59. (in Chinese)
[5] Barbe L, Bayle B, Mathelin M, et al. Bilateral controllers for teleoperated percutaneous interventions: evaluation and improements[C]∥2006Americancontrolconference. Minneapolis Minnesota. USA:[s.n.], 2006:3209-3214.
[6] 刘少强, 王爱民, 樊晓平, 等.实现比率遥操作系统稳定性与性能折衷的策略[J].控制理论与应用, 2005,22(4):661-665.
Liu Shaoqiang, Wang Aimin, Fan Xiaoping, et al. Control scheme for tradeoff between stability and performance in scaled telemanipulation[J].ControlTheory&Application, 2005, 22(4): 661-665. (in Chinese)
[7] 徐晶晶, 芮素波,曾庆军.网络遥操作机器人系统神经网络预测控制仿真研究[J]. 江苏科技大学学报:自然科学版,2008,22(1): 48-51.
Xu Jingjing, Rui Subo, Zeng Qingjun. Study on neural network predictive controller for telerobotics with variable time-delay[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2008, 22(1): 48-51. (in Chinese)
[8] 田小峰, 黄唯一, 宋爱国.力觉临场感遥操作机器人系统的时延稳定性分析[J].制造自动化,2001,8:15-17.
Tian Xiaofeng, Huang Weiyi, Song Aiguo, et al. Stability analysis of force telepresence teleoperation system with variable time-delay[J].ManufacturingAutomation, 2001, 8: 15-17. (in Chinese)
[9] Lawrence D A. Designing teleoperation architect-tures for transparency[C]∥ProceedingsofIEEEInternationalConferenceonRoboticsandAutomation. Nice France:[s.n.],1992.
[10] Anderson R J, Spong M W. Bilateral control of teleoperators with time delay[J].IEEETransactionsonAutomaticControl, 1989,34 (5): 494-501.
