基于APOS理论的三角形中位线的教学设计

2012-11-20浙江师范大学教师教育学院浙江金华321004

中学教研(数学) 2012年9期

关键词：位线中点四边形

● (浙江师范大学教师教育学院浙江金华 321004)

●童桂恒 (金华市第四中学浙江金华 321000)

基于APOS理论的三角形中位线的教学设计

●矫立娟(浙江师范大学教师教育学院浙江金华 321004)

●童桂恒(金华市第四中学浙江金华 321000)

1 教学背景

“三角形的中位线”是浙教版8年级数学下册第5章第6节的内容.本节课是在学生掌握四边形、梯形、平行线等内容的基础上，引出中位线的概念，进而探索研究它的性质，最后利用性质定理进行有关的论证和计算.本节课的内容步步衔接，层层深入，形成知识的链条.学好本课不仅为学习梯形中位线打下良好的基础，而且为今后学习证明线段平行和线段倍分关系提供了重要的方法和依据.可见，三角形中位线在整个知识体系中具有相当重要的位置，起到承上启下的作用.

2 教学目标

知识目标：理解三角形中位线的概念，知道三角形中位线和三角形中线的区别，理解掌握三角形中位线定理及得来的过程，并会运用它进行简单的计算、推理，提高解决问题的能力.

能力目标：通过对问题的探索、变式，使学生学会观察、分析、抽象、概括，培养学生分析问题、解决问题的能力.

情感、态度与价值观：通过剪、拼图形，激发学生兴趣，鼓励学习有困难的学生学好数学，帮助学生树立信心，使每一个学生能满腔热情地投入学习.

3 教学重点及难点

教学重点：三角形中位线定理.

教学难点：三角形中位线定理结论的证明及应用.

4 APOS视角下的教学过程

4.1 第1阶段——活动阶段

活动1让学生通过自己动手操作，形成对三角形中位线的初步认识.

教师：同学们，请拿出一张纸画一个三角形并把它剪下来.下面大家尝试：剪一刀将三角形剪成一张三角形纸片和一张梯形纸片，并将它们拼成一个四边形.

教师巡视全班，观察学生的操作情况.

教师：现在大家都完成了，请拼成了平行四边形的同学举手，说说你们是怎么做的？

通过学生们的叙述，总结出拼成平行四边形的条件：分别取三角形2条边的中点，联结2个中点，沿连线剪开，将所得的三角形和梯形拼接即得到平行四边形.

教师利用多媒体演示拼接过程，如图1所示.

图1

教师：以上述△ABC为例，我们称线段DE为△ABC的中位线.请大家思考一下，三角形中位线的定义是什么？

学生发言教师总结：联结三角形2条边的中点的线段叫三角形中位线.

活动2区分三角形中位线和三角形的中线.

教师：大家根据三角形中位线的定义，判断一个三角形有几条中位线？

学生：3条.

教师：那三角形的中位线与三角形的中线一样吗?

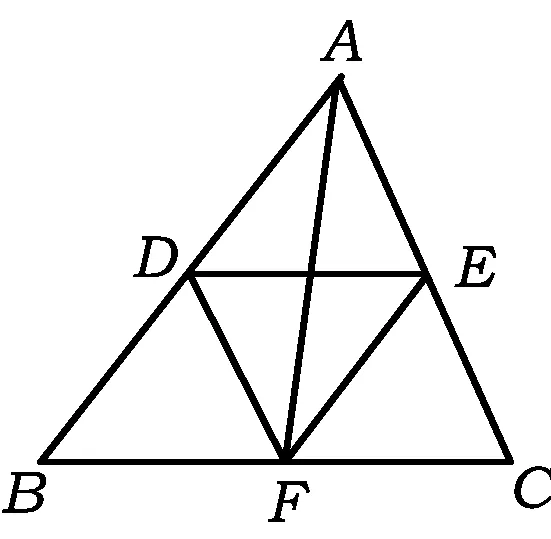
图2

学生回想三角形中线的定义，与中位线的定义进行比较.

教师用多媒体展示三角形的中位线DE,DF,EF和中线AF，如图2所示.

设计意图APOS理论中的“活动阶段”相当于观察、呈现数学概念的具体实体阶段，让学生对概念的形成过程有一个充分体验[1].本节课通过剪纸、拼图等活动唤起学生学习三角形中位线的兴趣，启发学生通过亲身体验主动建立三角形中位线的概念，为学习三角形中位线定理埋下伏笔.

4.2 第2阶段——过程阶段

教师：同学们，大家思考一下三角形的中位线和它所对应的边在位置上和数量上有什么关系？请大家进行小组讨论，如何证明你们的猜想是正确的(以图2为例说明).

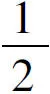
图3

证法1如图4，以点E为旋转中心，把△ADE绕点E，按顺时针方向旋转180°，得到△CFE,则点D,E，F同在一直线上，DE=EF，且△ADE≌△CFE,从而

∠ADE=∠F,AD=CF,

即

AB∥CF.

又因为

BD=AD=CF,

所以四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)，从而

DF∥BC(根据什么)，

即

DEBC.

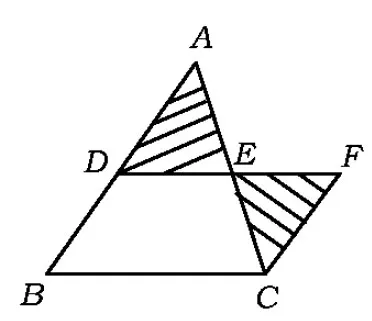
图4

图5

证法2如图5，延长DE至点F，使得EF=DE.因为AE=EC，∠AED=∠CEF,所以

△ADE≌△CFE,

即

AD=FC.

又因为

DB=AD,

所以

DBFC，

即四边形BCFD是平行四边形，从而

DEBC.

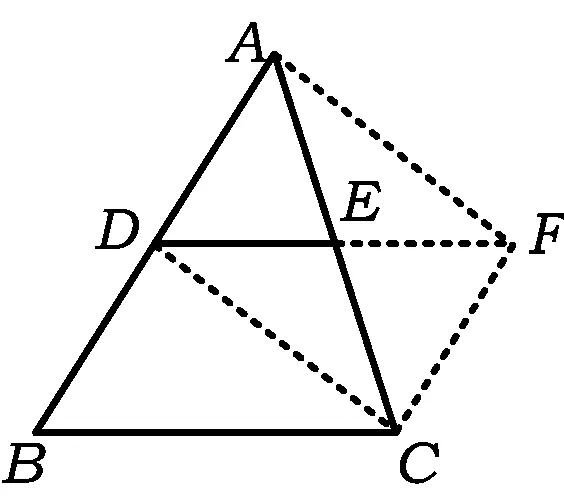
图6

证法3如图6，延长DE至点F，使得EF=DE.因为AE=EC,EF=DE,所以四边形ADCF是平行四边形,从而

ADFC,

即四边形DFCB是平行四边形，从而

DFBC,DEBC.

证法4过点C作AB的平行线交DE延长线于点F.因为CF∥AB,所以∠A=∠ECF.又因为AE=EC，∠AED=∠CEF,所以

△ADE≌△CFE,

即

AD=FC,DE=EF.

又因为

DB=AD,

所以

DBFC,

即四边形BCFD是平行四边形,从而

DEBC.

通过上述4种方法，验证了猜想是正确的.

设计意图APOS理论中的“过程阶段”是学生对具体实体进行思维概括并描述得出数学概念的阶段[1].学生通过之前的“活动”对三角形中位线的概念形成了初步的认知，在此基础上进行猜想并经过小组讨论，在教师的引导下验证猜想的正确性.同时，也为学生在以后的习题解答中添加辅助线提供了方案.

4.3 第3阶段——对象阶段

教师：哪位同学可以用文字语言把我们的猜想总结一下呢？

(学生回答，教师补充.)

教师：大家回答得非常好，刚才大家所说的就是今天所要学习的重点内容:三角形中位线定理.

三角形中位线定理：三角形的中位线平行于第3边，并且等于第3边的一半.

教师：同学们已经知道了三角形中位线定理的文字语言表述，现在请大家来思考一下如何用几何语言来表述？

几何语言：若DE是△ABC的中位线(或AD=BD，AE=CD),则DEBC.

设计意图APOS理论中的“对象”阶段，将过程看作是一个整体，并将其上升为一种意识，作为独立对象，认识到了概念的本质，对其赋予形式化的定义和符号，使其达到精致化，成为一个具体对象.从数学角度来看,由过程到对象的转移就是为从更高层次进行研究开拓了现实的可能性[2].在本节课中，教师引导学生通过“过程”的学习，抽象出三角形中位线定理的文字表达，以及符号表示，为以后解决类似问题作准备.

4.4 第4阶段——图示阶段

教师：现在我们一起来解决下面的问题.

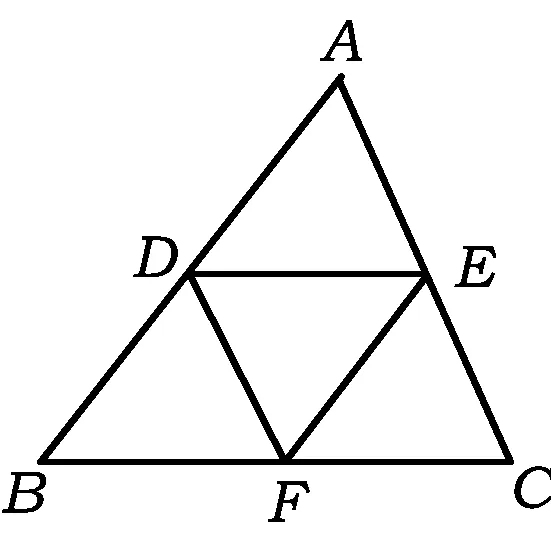
图7

1.如图7，已知D，E，F分别是△ABC的边AB,AC,BC的中点.

(1)若AB=6 cm，则EF=________cm；

(2)若∠ADE=60°，则∠B=________°；

(3)图中有几个平行四边形？

(4)你能证明△ADE,△EFC,△DBF,△DEF全等吗？

(5)若△ABC的周长为16，面积是12，则△DEF的周长为________，△DEF的面积为________.

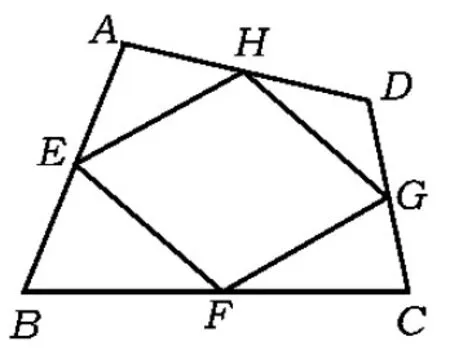
图8

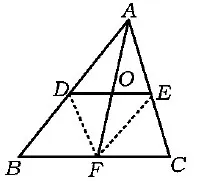
图9

2.如图8，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点.证明：四边形EFGH是平行四边形.

分析由E，F，G，H分别为四边形ABCD各边的中点，联想到应用三角形中位线定理来证明.有中点连线而无三角形，所以要作辅助线产生三角形(联结点A，C).

(经上述分析，让学生自己思考证明，并让2名学生在黑板上证明.)

3.如图9，DE是△ABC的中位线，AF是BC边上的中线，DE和AF交于点O.求证：DE与AF互相平分.

分析联结DF，EF，根据中位线的定理证明四边形ADEF是平行四边形.

设计意图个体对所有操作、过程和对象以及认知结构中与这个概念相关的其他概念进行相应的整合，在头脑中产生一个新的综合心理图式，这种图式能够对一些与概念相关联的问题是否属于该图式的范围作出判断，在个体的认知结构中占有特定地位.而且在后继的学习中会与其他的数学概念等相关知识建立起有意义的联系[3].学生通过具体练习，对三角形中位线定义及其定理的运用更加熟练、更加理解.