一类最值问题推广研究

● (兴化中学 江苏泰州 225700)

一类最值问题推广研究

●张乃贵(兴化中学 江苏泰州 225700)

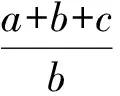
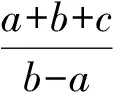
笔者首先从解题的方法上获得对问题的推广．

1 例1的推广

因为对于任意实数x都有f(x)≥0，所以a>0，b2-4ac≤0,b2≤4ac,c>0,从而

来探索、调控．

1.1 一般资料 2018年1月至 2018年6月，在海军军医大学（第二军医大学）东方肝胆外科医院泌尿外科行后腹腔镜下肾部分切除术治疗的肾脏腹侧肾肿瘤患者 15例，术中应用自制简易腹膜反折悬吊装置。其中男 9例、女 6例，平均年龄为（62.5±9.2）岁，肿瘤平均最大径为（2.9±1.0）cm，肿瘤位于右肾 7例、左肾 8例，均为位于肾脏腹侧的单发肿瘤，肿瘤分期均为 T1N0M0 期，R.E.N.A.L 评分为 6～10 分。无淋巴结、肾静脉或下腔静脉癌栓及远处转移。

因为b>a，所以

命题1已知二次函数f(x)=ax2+bx+c(b>a)，对于任意实数x都有f(x)≥0，则

2 例2和例3的推广

(1+λ1)[b-(λ1-1)a].

当b-(λ1-1)a>0时，

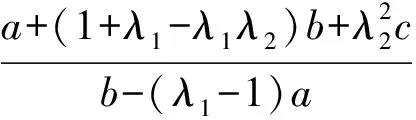
2λ1-λ2(λ1-1)>0，

即

2λ1+λ2-λ1λ2>0.

命题2已知二次函数f(x)=ax2+bx+c(其中b>(λ1-1)a)，对于任意实数x都有f(x)≥0，则

(λ1，λ2是正的常数且2λ1+λ2-λ1λ2>0的最小值为λ1+1．

如果对M，N中λ1，λ2赋予一些满足限制条件的新值，可以得到许多新题.笔者又从结构上对3个例题进行了推广．

3 例1～例3的推广

3个例题所求最小值的式子可统一为

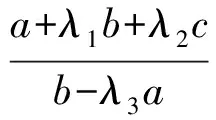
下面探求L的最小值及参数λ1,λ2,λ3的取值限制．

为了叙述简洁，限制参数满足条件λ1，λ2，b-λ3a>0，λ3≥0,可得命题3．

命题3已知二次函数f(x)=ax2+bx+c，对于任意实数x都有f(x)≥0，则

(λ1,λ2,b-λ3a>0,λ3≥0)的最小值为

[1]张乃贵．一个最值问题的探索课课堂实录[J]．上海中学数学，2005(1)：3-4．